
МУ по КР 3 семестр (1)
.pdf3
ЗАДАНИЕ на курсовую работу по курсу «Электротехника»
РАСЧЁТ ЧАСТОТНЫХ И ВРЕМЕННЫХ ХАРАКТЕРИСТИК ARC-ЦЕПЕЙ
1.АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ
1.1.Предполагая, что операционный усилитель (ОУ) идеальный, получить передаточную функцию H(p)=H(j ) в виде:
|
b p2 |
b |
p b |
|
H ( )e j ( ) . |
||||
H ( p) |
2 |
|
|
|
1 |
0 |
|
||
|
|
|
0 |
|
|
|
|||
|
p2 |
|
|
|
p 2 |
||||
|
|
|
|
||||||
|
|
|
Q |
|
|
0 |
|
||
|
|
|
|
|
|
|
|||
Рассчитать добротность Q, частоту 0 и коэффициенты b0, b1, b2. Вывести соотношения для амплитудно-частотной (АЧХ) H( ) и фазочастотной (ФЧХ)( ) характеристик цепи.
1.2.Построить на графике АЧХ и ФЧХ, выбрать частотный интервал для последующего анализа на ЭВМ.
1.3.Для заданной цепи составить и нарисовать эквивалентную схему, заменив реальный ОУ его низкочастотной схемой замещения с параметрами:
rВХ = 50 кОм, rВЫХ = 0,2 кОм, k =250.
1.4. Рассчитать АЧХ и ФЧХ цепи с реальным ОУ на ЭВМ. Построить полученные зависимости на графике п. 1.2.
2.АНАЛИЗ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ЦЕПИ
2.1.Предполагая, что ОУ идеальный, вывести формулы для переходной h(t) характеристики цепи:
а) с использованием уравнений состояния и их решения во временной области;
б) с применением преобразования Лапласа.
2.2.Построить на графике зависимость h(t) и выбрать временной интервал для анализа цепи на ЭВМ.
2.3.Провести расчёт переходной характеристики h(t) исходной цепи (с реальным ОУ) на ЭВМ при заданных параметрах элементов исходной схемы. Построить полученную характеристику на графике п. 2.2.
2.4.Используя полученную в п. 2.1 переходную функцию, рассчитать форму выходного сигнала при воздействии на вход прямоугольного импульса (параметры импульса задаются преподавателем).
E = 5 – 0,1 N, (B) где N ― номер по журналу;
tИ=0,8 Ткон .
Варианты расчетных схем находятся у преподавателя.

4
Пример расчета
3.АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ
3.1. Расчёт схемы для случая идеального ОУ
Исходные данные:
R1 = 14,3 кОм, R3 = 76,5 кОм,
С1 = 2 нФ, С2 = 1 нФ,
UВХ(t) = 1sinωt, В.
Рис. 1. Исходная схема
Так как операционный усилитель (ОУ) – идеальный, то его электрофи-
зическая модель предполагает, что RВХ ОУ = ∞, RВЫХ ОУ = 0, k → ∞ и эквивалентная схема для расчета (рис. 2) будет выглядеть следующим образом:
Рис. 2. Расчётная схема для составления уравнений по МУП
k = ∞, U2 = φ2.
Составим уравнения по методу узловых потенциалов (МУП) (все расчёты проводятся для параметров в комплексной форме) [1], [2]:

5
|
g1 p(C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
C2 ) 1 pC2 2 |
pC1 3 |
U ВХ g1, |
|
|
(1) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
pC2 |
1 (g3 |
|
pC2 ) 2 |
g3 3 |
0, |
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2) → |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
pC2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(g1 p(C1 |
|
C2 ))g3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(1) → |
|
|
|
pC |
|
U ВХ g . |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
pC2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решаем (1) относительно потенциала 3 и записываем выражение для |
|||||||||||||||||||||||||||||||||||||
комплексной передаточной функции: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
H ( p) |
U ВЫХ |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
pC2 g1 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
p2C C |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
pg |
3 |
(C C |
2 |
) g g |
3 |
|
|||||||||
|
|
|
|
|
|
U ВХ |
|
|
U ВХ |
|
|
|
|
1 |
|
|
|
1 |
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
g1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
p2 |
|
|
|
g |
3 |
(C C |
2 |
) |
|
|
|
g g |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
p |
|
|
|
|
1 |
|
|
|
|
|
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
C1C2 |
|
|
|
|
C1C2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Получили передаточную функцию (ПФ) в каноническом виде полосно - пропускающего фильтра (ППФ) второго порядка.
Найдём резонансную частоту и добротность фильтра:
2 |
|
g1g3 |
|
1 |
|
1 |
4,57 108 ( |
рад |
)2 , |
|
|
|
|
||||||
0 |
|
C1C2 |
|
R1R3C1C2 |
|
14,3 76,5 2 10 12 |
|
с |
|
|
|
|
|
|
|||||
0 
 4,57 108 2,138 104 радс ,
4,57 108 2,138 104 радс ,
f0 0 = 3,404 кГц ― резонансная частота.
2
|
|
|
|
g |
(C C |
) |
|
|
0 |
C C |
|
2,138 104 |
2 10 18 76,5 103 |
|
|
0 |
|
|
3 |
1 2 |
|
Q |
|
1 2 |
|
|
|
=1,09, |
|
Q |
|
|
C1C2 |
|
g3 (C1 C2 ) |
|
3 10 9 |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
Q = 1,09 ― добротность фильтра. |
|
|
|
|
|||||||
Величина коэффициентов передаточной функции: |
|
|
||||||||||||
а |
|
0 |
|
2,138 104 |
|
1,9615 104 |
рад |
, |
|||
|
|
|
|
|
|
|
|||||
1 |
Q |
|
1,09 |
|
|
|
с |
|
|||
|
|
|
|
|
|
||||||
b |
g1 |
|
|
1 |
3,496 104 . |
||||||
|
|
|
|
||||||||
1 |
|
C1 |
|
14,3 103 2 10 9 |
|
|
|
||||
|
|
|
|
|
|
||||||
Таким образом, передаточная функция принимает вид:

|
|
|
|
6 |
|
|
|
|
b p |
|
3,496 104 p |
||
H ( p) |
|
1 |
|
|
|
. |
p2 |
0 |
p 2 |
p2 1,9615 104 p 4,57 108 |
|||
|
|
Q |
0 |
|
|
|
|
|
|
|
|
|
|
Запишем выражение для комплексной передаточной функции в явном виде в зависимости от частоты:
p j , |
|
|
|
|
|
H ( j ) |
b1 j |
|
. |
||
2 j |
0 2 |
||||
|
|
||||
|
|
Q |
0 |
|
|
|
|
|
|
||
Получим математические выражения для АЧХ и ФЧХ фильтра в общем
виде:
H ( ) |
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
― АЧХ фильтра. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
( 2 2 )2 |
|
( |
)2 |
|||||||||
|
|
|
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
||
90 |
arctg |
|
|
|
|
, |
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 2 |
|
|
0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
( ) |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
― ФЧХ фильтра. |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
||
270 |
|
|
arctg |
|
|
|
|
, |
|
0 |
||||||
|
|
2 |
|
|
2 |
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
Графики АЧХ и ФЧХ удобно строить в системе DESIGN LAB 8.0 [4]. Расчётная схема для идеального ОУ представлена на рис. 3:
Рис. 3. Изображение, полученное в результате вычерчивания

7
схемы на экране дисплея
При составлении задания на анализ окно должно выглядеть так:
Рис. 4. Окно задания режима частотного анализа
Этим мы задаём режим частотного анализа схемы. Далее необходимо определить частотный диапазон, исходя из рассчитанных значений резонансной частоты и типа фильтра. Диапазон можно менять несколько раз, пока характеристики не достигнут своих установившихся значений.
Рис. 5. Окно определения частотного диапазона
После задания расчётного режима нужно нажать на кнопку F11 и на экране дисплея должен появиться график АЧХ. Если этого не происходит автоматически, то надо проделать следующее: щёлкнуть левой кнопкой мыши по позиции Plot горизонтального меню. В появившемся вертикальном меню выделить строку Add Y Axis, щелкнув по ней левой кнопкой мыши. После этого на экране появляется вертикальная ось.

8
Рис. 6. АЧХ и ФЧХ исследуемой схемы для случая идеального ОУ
В позиции горизонтального меню Trace выбираем в появившемся меню строчку Add и в появившемся правом окне Function or Macros щелчком левой кнопки мыши выделяем функцию выделения амплитуды М( ). В нижней части панели в строке Trace Expression для указания того, амплитуда какого напряжения должна быть выведена, щёлкаем левой кнопкой мыши по строке V(1) в левом окне Simulation Output Variables. В нижней строке оказывается сформированной функция М(V(1)). Это соответствует выводу графика АЧХ напряжения V(1). Щёлкаем по кнопке мыши и на экране появляется график. Все эти операции нужно проделать и для получения графика ФЧХ. Только вместо выделения функции М( ) необходимо выделить функцию фазы P( ). После этого на экране появляется “картинка” совмещённых графиков АЧХ и ФЧХ напряжения V(1) (рис. 6). Эти графики надо вывести на печать и представить преподавателю в качестве решения для расчёта частотных характеристик для схемы с идеальным ОУ. На данном графике маркером выделена резонансная частота f0 = 3,396 кГц, что практически совпадает с расчётной.
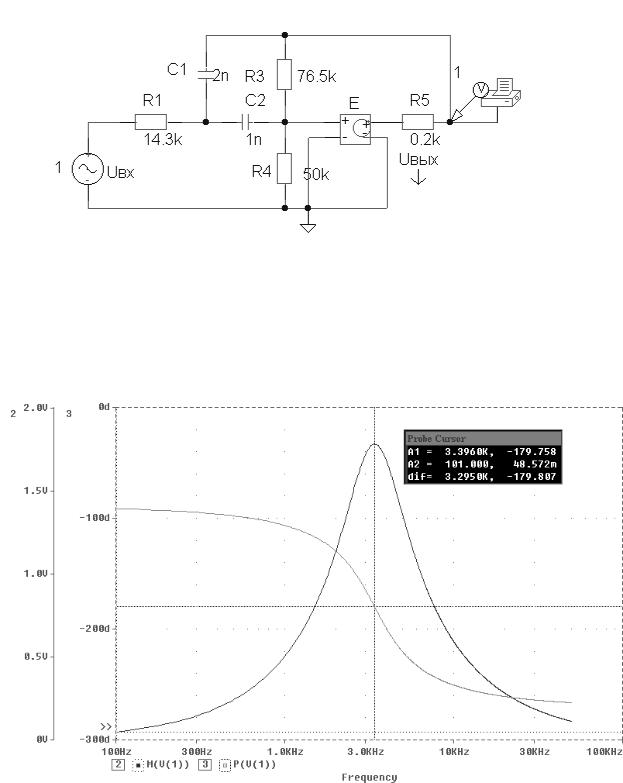
9
3.2. Расчёт схемы при реальном ОУ
Для реального ОУ расчёт частотных характеристик производится только с помощью ЭВМ. Для этого необходимо внести изменения в расчётную схему, представленную на рис. 7:
Рис. 7. Исследуемая схема для реального ОУ
Как видно из схемы добавились параметры ОУ: RВХ ОУ = 50 кОм и RВЫХ ОУ = 0,2 кОм. Кроме этого, коэффициент усиления ОУ k = 250. Режим анализа схемы задается аналогично п. 1.1 и получаем решение в виде графиков АЧХ и ФЧХ реального фильтра, изображенных на рис. 8:
Рис. 8. АЧХ и ФЧХ исследуемой схемы для случая реального ОУ
Как видно, графики, представленные на рис. 6 и рис. 8, практически совпадают. На этом анализ частотных характеристик схемы завершён.

10
4.АНАЛИЗ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ЦЕПИ
4.1.Составление уравнений состояния для схемы с идеальным ОУ
Изобразим схему для составления уравнений состояния (УС) с учётом того, что ОУ ― идеальный [3]:
Исходные данные:
Е =1 В,
Uc1(0) = 0 В, Uc2(0) = 0 В,
U2 = φ2 .
Рис. 9. Расчётная схема для составления УС
Примечание:
Для схем с обратной связью уравнения состояния удобнее составлять по методу наложения.
Рассматриваемая схема в исходном варианте не содержит обратную связь, поэтому уравнения состояния составим с использованием расширенных узловых уравнений:
g1 1 ic1 ic2 |
U ВХ g1, |
(1) |
||||||||||||||
g |
3 |
|
2 |
g |
|
3 |
i |
0, |
(2) |
|||||||
|
|
|
|
|
|
3 |
|
|
|
|
c2 |
|
|
|||
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
U |
|
|
, |
|
|
(4) |
||||
|
|
|
3 |
c1 |
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
U |
c2 |
. |
|
|
(5) |
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
Решим систему относительно токов ic1 и ic2. С учётом (3) система упрощается:
(5) φ1 = Uc2,
(4) φ3 = Uc2 − Uc1,
(2) ic2 = −g3 φ3 = − g3(Uc2 − Uc1) = g3Uc1 − g3Uc2,
(1) ic1 = UВХg1 − ic2 − g1 φ1 = UВХg1 − g3Uc1 + g3Uc2 − g1 Uc2 = − g3Uc1 +
+(g3 – g1) Uc2 + UВХg1.
Так как i |
|
C |
dUc1 |
, |
i |
C |
dUc2 |
, то уравнения состояния примут вид: |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
c1 |
|
|
|
|
|
|
dt |
c2 |
|
|
|
|
|
dt |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
dU |
c1 |
|
|
|
|
g |
3 |
|
|
|
|
|
g |
3 |
g |
1 |
|
|
g |
|||||
|
|
|
|
|
Uc1 |
|
|
|
|
|
Uc2 |
1 |
U ВХ , |
|||||||||||
|
|
|
|
|
|
|
|
C1 |
|
|
||||||||||||||
|
dt |
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
C1 |
||||||||
|
dUc2 |
|
|
|
g3 |
|
|
|
|
g3 |
|
|
|
|
|
|
|
|
||||||
|
|
|
Uc1 |
U c2 0 U ВХ . |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
dt |
|
|
|
|
C2 |
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

11
|
|
g3 |
|
g3 g1 |
|
|
|
g1 |
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
A1 |
C1 |
|
C1 |
|
, B1 |
|
. |
|||||||
|
|
|
|
|
C |
|
||||||||
|
|
g3 |
|
|
g3 |
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
C2 |
|
C2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Численные значения коэффициентов матриц А1 и В1 для рассматриваемого примера равны:
А |
6,536 103 |
28,429 103 |
, |
В |
34,965 103 |
. |
||||||||||||
1 |
|
|
13,072 103 |
13,072 103 |
|
1 |
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
Составим характеристическое уравнение: |
|
|
||||||||||||||||
det(λ·1 – A1) = 0, |
|
|
|
|
|
|
||||||||||||
|
|
g3 |
|
g1 g3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
C1 |
|
C1 |
|
|
0 . |
|
|
|
|
|
|||||||
|
|
g3 |
|
|
g3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
C2 |
|
|
C2 |
|
|
|
|
|
|
|
|
|
|||||
По правилу расчёта определителя получаем квадратное уравнение:
2 |
g |
3 |
|
g |
3 |
|
|
g 2 |
|
g |
( g |
g |
3 |
) |
|
|||
|
|
|
|
3 |
|
3 |
1 |
|
|
|
0, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
C2 |
|
C1 |
|
|
C1C2 |
|
|
C1C2 |
|
|
|
|
|||||
2 |
g3( C1 C2 ) |
|
g1g3 |
0. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
C1C2 |
|
|
|
|
C1C2 |
|
|
|
|
|
|
|
|
||
Характеристическое уравнение совпадает по виду со знаменателем передаточной функции H(p), полученной в первой части расчёта. После подстановки чисел получаем следующее характеристическое уравнение (ХУ):
2 |
1,9615 10 4 4,57 108 0. |
|
|
|
|
|||||
Найдём его корни: |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
1,9615 104 |
j |
(1,9615 104 )2 4 4,57 108 |
|
|
||||
1,2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0,98075 104 j1,8995 104 j |
СВ |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Так как корни ХУ получились комплексно-сопряженные, то вид решения для напряжений на конденсаторах запишется следующим образом:
Uc1(t) Uc1уст А1е t sin( СВt 1), Uc2 (t) Uc2уст А2е t sin( СВt 2 ).
Напряжение на выходе схемы вычисляется по формуле:
3 UВЫХ (t) Uc2 Uc1 .
Составим схему для установившегося режима (рис. 10):

12
Uc2уст=UВХ,
Uc1уст=UВХ.
Рис. 10. Расчётная схема для установившегося режима
Рассмотрим момент времени t = 0+. УС примут вид:
dUc1 |
|
|
|
0 |
|
|
g1 |
|
|
34,965 10 |
3 |
В/c |
|
|
|
|
|
|
|
|
|
||||||
dt |
|
|
A1 |
|
|
|
U ВХ |
1(t) . |
|||||
|
|
|
C |
|
|
||||||||
dUc2 |
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
dt |
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Система для поиска неизвестных коэффициентов в выражении для Uc1(t) примет следующий вид:
|
(0) 0 1 A1 sin 1, |
A1 |
1 |
|
|
|
||||
U c1 |
|
, |
|
|||||||
sin 1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
dU c1 |
0,98075 10 |
4 |
A1 sin 1 1,8995 10 |
4 |
A1 cos 1 |
|||||
|
|
|
|
|
||||||
dt |
|
|
|
|
|
|
|
|
|
|
Решая эту систему, получаем:
γ1 = −37,05˚, А1 = 1,6596 В.
Вид решения для напряжения на конденсаторе С1:
Uc1(t) 1 1,6596e 0,98 104 t sin(1,8995 104 t 37,05 )
3,4965 104.
1(t), В.
Система для поиска неизвестных коэффициентов в выражении для Uc2(t) примет следующий вид:
|
(0) 0 1 A2 sin |
2 , |
|
|
|
1 |
|
|
||||
U c2 |
A2 |
|
, |
|
||||||||
sin 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
dUc2 |
0,98075 |
10 |
4 |
A2 sin 2 |
1,8995 10 |
4 |
A2 cos |
|||||
|
|
|
|
|
||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
Решая эту систему, получаем:
γ2 = 62,59˚, А2 = −1,1254 В.
Вид решения для напряжения на конденсаторе С2:
Uc2 (t) 1 1,1254e 0,98 104 t sin(1,8995 104 t 62,59
2 0.
) 1(t), В.
