
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ
ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ
(МТУСИ)
Кафедра теории электрических цепей
Лабораторная работа №13
«Спектральный анализ сигналов
с применением ДПФ»
Выполнил студент группы ********* _______________ ***********
Проверил ________________________ ********
Москва 2005
Цель работы
С помощью программы Micro-Cap получить дискретные спектры различных импульсных сигналов с использованием аппарата дискретного преобразования Фурье (ДПФ).
Предварительные расчеты
Найти непрерывную спектральную плотность F(jω) прямоугольного импульса.
 B,
где
B,
где
t — время;
τ = 1 мс — длительность импульса;
U = 4 B — амплитуда импульса;
Спектральная плотность этого сигнала будет равна:
F(jω)
=


// Расчеты выполнены в программе Scilab 6.1.0
// Лабораторная работа № 13
// Выполнил студент группы ***************************
// Непрерывная спектральная плотность прямоугольного импульса
// Длительность импульса, с
t = 10^-3;
// Амплитуда импульса, B
U = 4;
// Частота, Гц
fmax = 1/t;
f = 0:fmax/100:5*fmax;
F1 = (2*U./(2*%pi.*f)).*abs(sin(2*%pi.*f.*(t/2)));
plot(f,F1)
xgrid()
xtitle('Модуль непрерывной спектральной плотности','f,Гц','|F(jw)|,Bc')
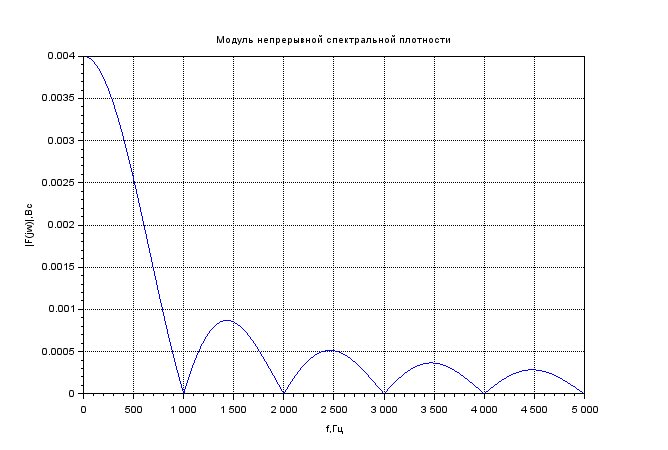
Найти непрерывную спектральную плотность F(jω) серии из трех прямоугольных импульсов.
Т = 0,4 мс — период;
τ = 0,1 мс — длительность импульса;
U = 1 B — амплитуда импульса;
Спектральная плотность этого сигнала (по теоремам линейности и запаздывания) будет равна:
F(jω)
= F1(jω)( ),
где F1(jω)
=
),
где F1(jω)
=
 — спектральная плотность первого
импульса в пачке.
— спектральная плотность первого
импульса в пачке.
// Непрерывная спектральная плотность серии из трех прямоугольных импульсов
// Длительность импульса, с
t = 0.1*10^-3;
// Амплитуда импульса, B
U = 1;
// Период, с
T = 0.4*10^-3;
// Частота, Гц
fmax = 1/T;
f = 0:fmax/100:2*fmax;
F2 = (2*U./(2*%pi.*f)).*sin(2*%pi.*f.*(t/2)).*(1+exp(-%i*2*%pi.*f.*T)+exp(-%i*2*2*%pi.*f.*T));
plot(f,F2)
xgrid()
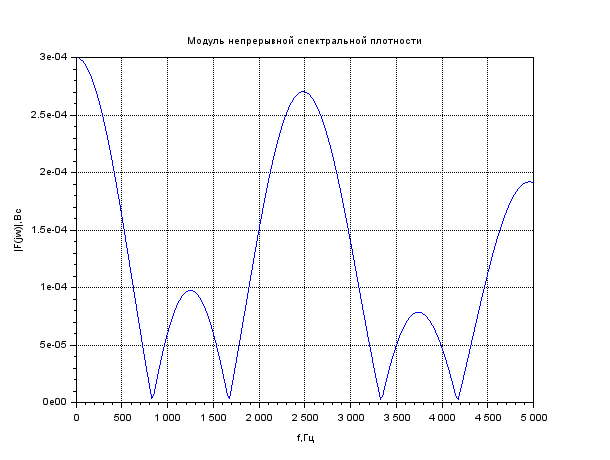 xtitle('Модуль
непрерывной
спектральной
плотности','f,Гц','|F(jw)|,Bc')
xtitle('Модуль
непрерывной
спектральной
плотности','f,Гц','|F(jw)|,Bc')
Найти непрерывную спектральную плотность затухающей синусоиды.
t — время;
a = 800 1/c — коэффициент;
ω1 = 8000 рад/c — угловая частота;
Спектральная плотность данного сигнала равна:
F(jω)
=

// Коэффициент a, 1/c
a = 800;
// Угловая частота, рад/c
w1 = 8000;
f = 0:100:5000;
// Спектральная плотность
F3 = w1./((a + %i*2*%pi.*f)^2 + w1^2);
plot(f,abs(F3))
xgrid()
xtitle('Модуль непрерывной спектральной плотности','f,Гц','|F(jw)|,Bc')
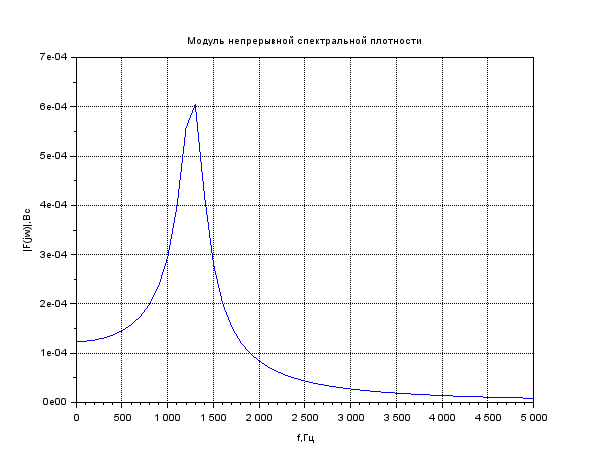 Найти
непрерывную спектральную плотность
F(jω)
прямоугольного радиоимпульса,
образованного отрезком синусоиды.
Найти
непрерывную спектральную плотность
F(jω)
прямоугольного радиоимпульса,
образованного отрезком синусоиды.
Спектральная плотность данного сигнала равна:
F(jω) =

// Спектральная плотность
F4 = (w1./(w1^2 - (2.*%pi.*f).^2)).*(1 - exp(-%i.*(2*%pi.*f./w1).*2.*%pi));
plot(f,abs(F4))
xgrid()
xtitle('Модуль непрерывной спектральной плотности','f,Гц','|F(jw)|,Bc')

Найти непрерывную спектральную плотность F(jω) серии из трех прямоугольных радиоимпульсов
ω1 = 8000 рад/c — угловая частота;
T1 = 2π/ω1 c — период синусоиды;
τ = nT1 — длительность импульса;
n = 3 — целое число периодов за время τ;
T = 4T1 — период;
F(jω) = F1(jω)( ), где F1(jω) = — спектральная плотность первого импульса в пачке.
// Угловая частота, рад/c
w1 = 8000;
// Период синусоиды
T1 = 2*%pi/w1;
//Длительность импульса, с
n = 3; t = n*T1;
// Период, с
T = 4*T1;
// Спектральная плотность
F5 =(w1./(w1^2 - (2.*%pi.*f).^2)).*(1 - exp(-%i.*(2*%pi.*f./w1).*n.*2.*%pi)).*(1+exp(-%i*2*%pi.*f.*T)+exp(-%i*2*2*%pi.*f.*T));
plot(f,abs(F5))
xgrid()
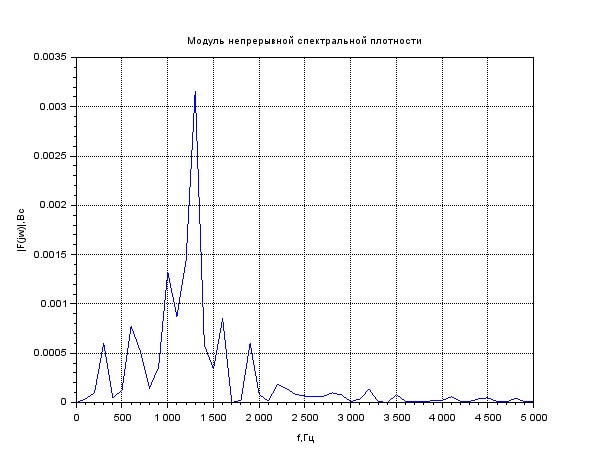 xtitle('Модуль
непрерывной спектральной
плотности','f,Гц','|F(jw)|,Bc')
xtitle('Модуль
непрерывной спектральной
плотности','f,Гц','|F(jw)|,Bc')
Машинный эксперимент



Спектральная плотность прямоугольного импульса
F(jω), Вс
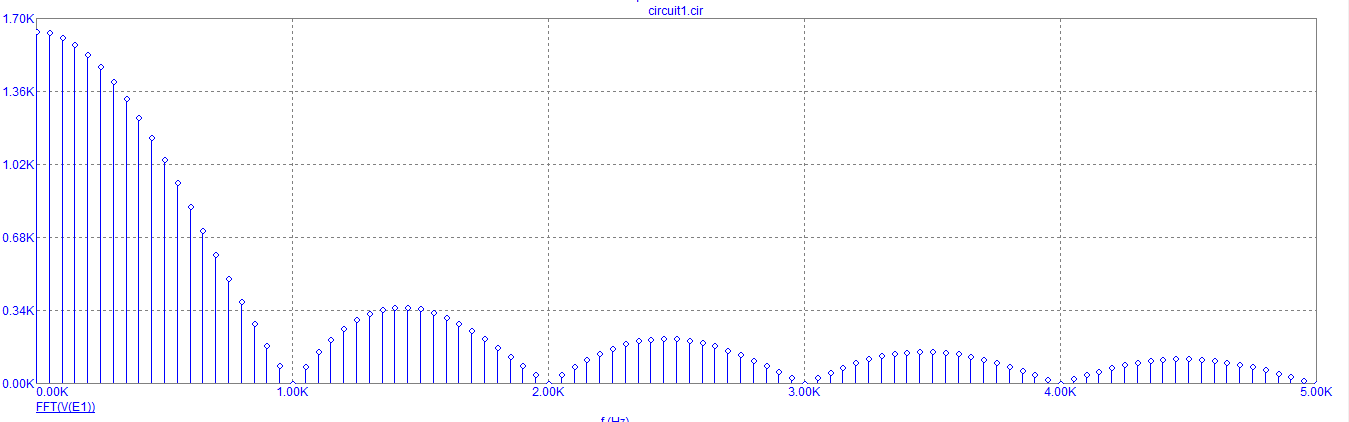
f, Гц
Спектральная плотность серии из трех прямоугольных импульсов
F(jω), Вс
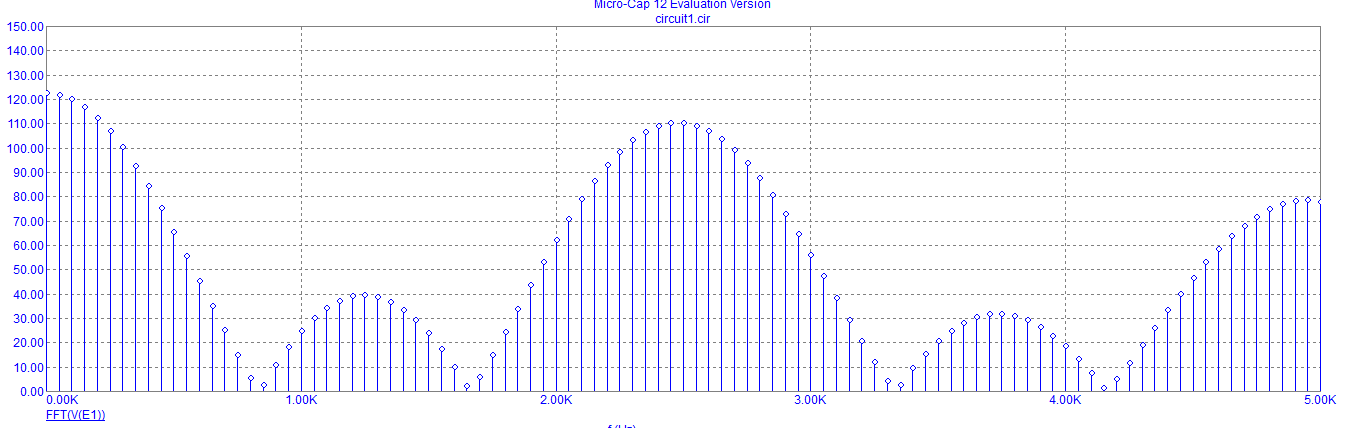
f, Гц
Спектральная плотность затухающей синусоиды
F(jω), Вс
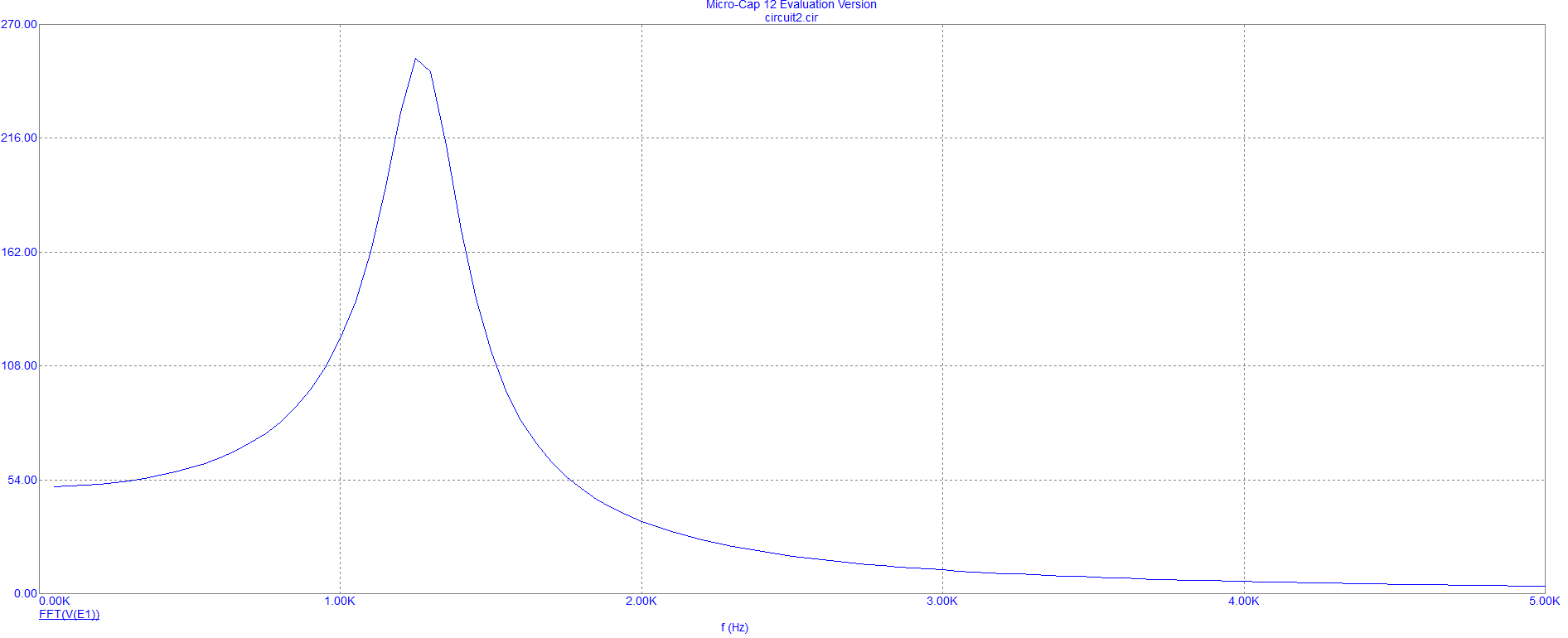
f, Гц
Спектральная плотность отрезка синусоиды
F(jω), Вс
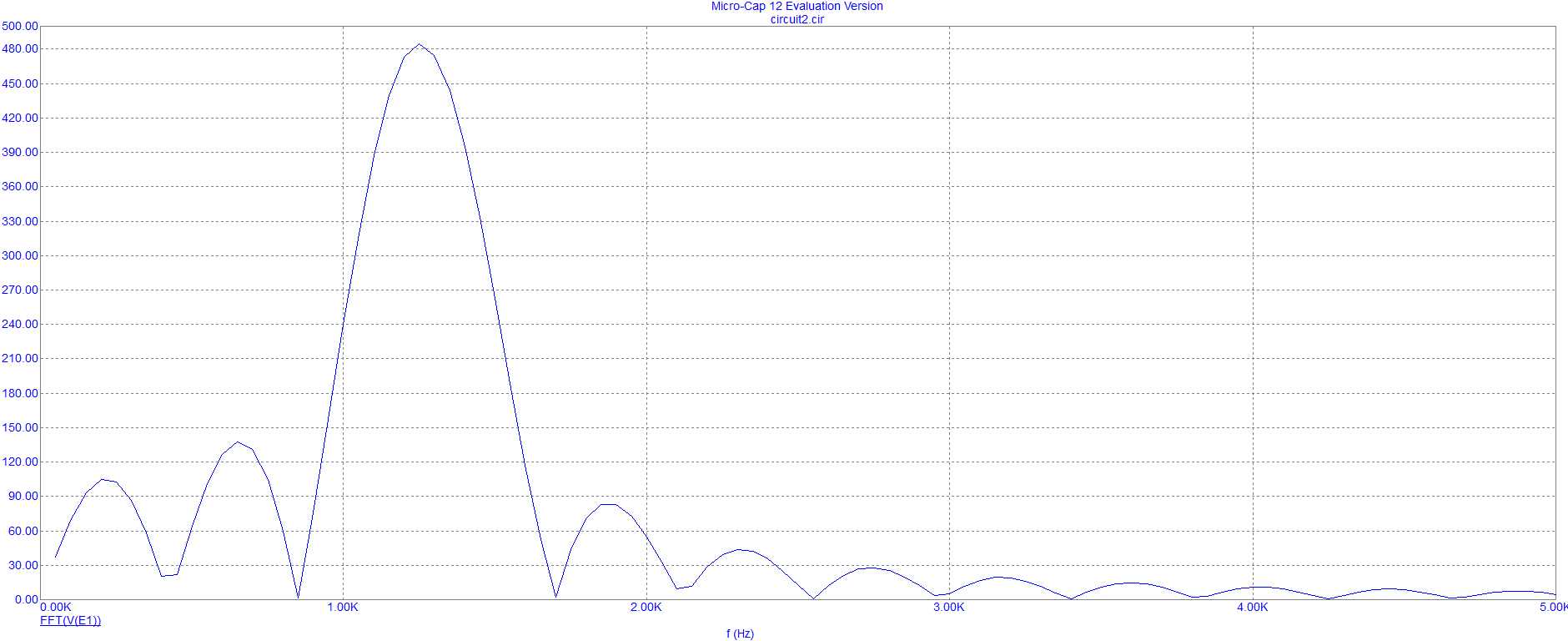
f, Гц
Спектральная плотность серии из трех отрезков синусоиды
F(jω), Вс

f, Гц
Вывод: Графики, полученные в процессе машинного эксперимента, совпадают с графиками, полученными при предварительных расчетах. Это означает, что предварительные расчеты проведены правильно.
Контрольные вопросы:
Что называется непрерывным и дискретным преобразованием Фурье (ДПФ)?
Ответ: 1) Непрерывным преобразованием называется преобразование вида:
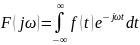
2) Дискретным преобразованием Фурье называется преобразование вида:

где X(kω) — спектр дискретного сигнала;
ω = 2π/NT — основная частота преобразования;
Какими свойствами обладает непрерывное преобразование Фурье?
Ответ: 1) Теорема запаздывания — Если функции f(t) соответствует спектральная плотность F(jω), то функции f(t – t0) соответствует спектральная плотность F(jω)e-jωt0.
2)
Теорема масштабирования — Если функции
f(t)
соответствует спектральная плотность
F(jω),
то функции f(kT)
соответствует спектральная плотность
(1/k)F( ),
где k
— произвольная константа.
),
где k
— произвольная константа.
Какими свойствами обладает ДПФ?
Ответ: Периодичность и симметричность
Что называется дискретными свертками?
Ответ: Выражения вида:
f1(k)
=
 и f1(k)
=
и f1(k)
=

Что называется быстрым преобразованием Фурье (БПФ)?
Ответ:
Быстрое
преобразование Фурье
— это метод, позволяющий вычислять ДПФ
за время ![]() .
Этот метод основывается на свойствах
комплексных корней из единицы (а именно,
на том, что степени одних корней дают
другие корни).
.
Этот метод основывается на свойствах
комплексных корней из единицы (а именно,
на том, что степени одних корней дают
другие корни).
Основная идея БПФ заключается в разделении вектора коэффициентов на два вектора, рекурсивном вычислении ДПФ для них, и объединении результатов в одно БПФ.
Итак,
пусть имеется многочлен ![]() степени
степени ![]() ,
где
—
степень двойки, и
,
где
—
степень двойки, и ![]() :
:

Многочлены ![]() и
и ![]() имеют
вдвое меньшую степень, чем многочлен
имеют
вдвое меньшую степень, чем многочлен ![]() .
Если мы сможем за линейное время по
вычисленным
.
Если мы сможем за линейное время по
вычисленным ![]() и
и ![]() вычислить
вычислить ![]() ,
то мы и получим искомый алгоритм быстрого
преобразования Фурье (т.к. это стандартная
схема алгоритма "разделяй и властвуй",
и для неё известна асимптотическая
оценка
).
,
то мы и получим искомый алгоритм быстрого
преобразования Фурье (т.к. это стандартная
схема алгоритма "разделяй и властвуй",
и для неё известна асимптотическая
оценка
).
Итак,
пусть мы имеем вычисленные вектора ![]() и
и ![]() .
Найдём выражения для
.
Найдём выражения для ![]() .
.
Во-первых, вспоминая (1), мы сразу получаем значения для первой половины коэффициентов:

