Лабораторные работы / ТЭЦ лабораторная №24а

ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ (МТУСИ)

Кафедра теории электрических цепей Лабораторная работа №24а «Исследование на ЭВМ спектров периодических негармонических сигналов»

Выполнил студент группы **********___________________ ***********

Проверил ____________________ *******

Москва 2001

Цель работы: С помощью машинного эксперимента изучить спектральный состав периодических негармонических сигналов.

Предварительный расчет:

1. Построить кривую на отрезке времени 0≤t≤1 мкс, мгновенное значение которой определяется выражением

--> f1=10^6;

--> t=0:1*10^(-8):1*10^(-6);

--> function [y]=u(t)

> y=2+5*sin(2*%pi*f1*t)+3*sin(3*2*%pi*f1*t)

> endfunction

--> plot(u(t))

--> xgrid();

--> mtlb_hold('on');

--> xtitle(' Построить кривую на отрезке времени 0≤t≤1 мкс','t','U(t)');

--> legend('u(t)',-1);

2. Построить амплитудный дискретный спектр этого сигнала.

--> f1=10^6;

--> ff=[0,f1,2*f1,3*f1];

--> um=[2 5 0 3];

--> plot2d3(ff,um)

--> xgrid();

--> mtlb_hold('on');

--> xtitle('Построить амплитудный дискретный спектр этого сигнала');

3. Нарисовать в масштабе спектр однополупериодного сигнала

--> f=100;

--> w1=2*%pi*f;

--> T=1/f;

--> t=[0:T/100:T];

--> Um=100;

--> tau=T/2;

--> u1=Um*sin(2*%pi*f*t).*(t>=0).*(t<=tau);

--> subplot(211)

--> plot(t,u1)

--> xtitle('Однополупериодный сигнал','t, c','u(t), B');

--> n=100;

--> a=0;

--> b=T;

--> h=(b-a)/n;

--> t=[a:h:b];

--> y1=(1/T)*u1;

--> A0=inttrap(t,y1);

--> F(1)=A0;

--> ng=5;

--> for n1=1:ng

> y2=(2/T)*cos(n1*w1*t).*u1;

> A=inttrap(t,y2);

> y3=(2/T)*sin(n1*w1*t).*u1;

> B=inttrap(t,y3);

> C=sqrt(A^2+B^2);

> F(n1+1)=C;

> end

--> n2=0:1:ng;

--> subplot(212)

--> xtitle('Амплитудный дискретный спектр','k','Umk,B');

--> plot2d3(n2,F)

Часть 1. Схема эксперимента:

Н егармонический переодический сигнал 2+5.0*sin(2*PI*1E6*t)+1.0*sin(3*2*PI*1E6*t)

u(t), В

Зависимость мгновенного напряжения генератора на отрезке времени и его дискретный амплитудный спектр:

t, мкс

U_k

f, Гц

u(t), В

Та же зависимость при изменении амплитуды 3 гармоники на 1 В

f, МГц

U_k

t, мкс

Часть 2. Схема эксперимента:

Простейшая выпрямительная схема состоящая из источника синусоидального напряжения Sine Source с амплитудой 100 В и частотой 100 Гц, полупроводникового диода и резистора 10 кОм.

u(t), В

Зависимость мгновенного напряжения генератора от времени

t, мс

u(t), В

Зависимость мгновенного напряжения на резисторе от времени

t, мс

U_k

Дискретный спектр напряжения на резисторе

f, Гц

Вывод:

Кривые напряжений и спектров, полученные в предварительном расчете совпадают с теми кривыми напряжений и спектрами, которые были получены в программной среде Micro-cap. Мы видим, что при изменении амплитуды третьей гармоники на единицу изменяется и кривая напряжения, и дискретный импульс.

Любая форма сигнала может быть представлена как сумма гармонических составляющих с определенной амплитудой и начальными фазами.

Вопросы для самопроверки:

1. Что такое спектр напряжения?

Спект напряжения – совокупность гармонических составляющих на напряжения, на которые раскладывается сигнал.

2. Почему анализируемые напряжения имеют дискретный спектр?

Потому что они представлены в виде ряда с ограниченным числом гармоник.

3. Запишите ряд Фурье и назовите его составляющие.

,

где

- постоянная составляющая

, k=1,2,3…

, - гармоники с частотами кратными частоте

- основная частота (частота первой гармонической составляющей)

-произвольный момент времени (обычно )

Т- период функции

k- номер коэффициента разложения (номер гармонической составляющей)

-частоты высших гармонических составляющих (k=2,3,4…)

Или в тригонометрической форме:

где

–спектр амплитуд

- спектр фаз

Формула ряда Фурье в комплексной форме

где -комплексная амплитуда k-й гармоники

– амплитуда k-й гармоники

- начальная фаза k-й гармоники

4. Что представляет собой равенство Парсеваля?

Равенство Парсеваля широко используется в теории цепей и сигналов при выборе полосы пропускания канала связи, обеспечивающей наилучшее использование энергии сигнала.

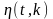- мощность элементарных функций по которым определен спектр сигнала. Мощность гармонических функций равна ½.

Равенство Парсеваля показывает, что активная мощность периодического негармонического сигнала равна сумме мощностей всех составляющих его обобщенного спектра.