3.2 Критерий Рауса

Для определения устойчивости замкнутой системы воспользуемся критерием Рауса. Для формулировки этого критерия используется таблица Рауса (рисунок 10).

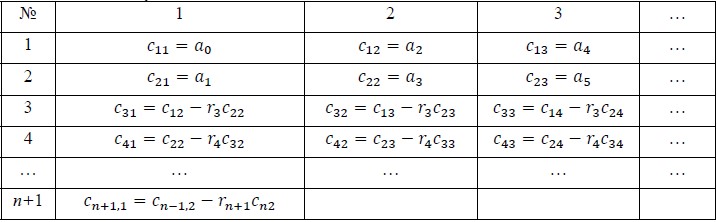
Рисунок 10 – Коэффициенты таблицы Рауса

В первой строке выписываются коэффициенты характеристического полинома с четными индексами, а во второй строке – коэффициенты с нечетными индексами в порядке их возрастания. Элементы последующих строк вычисляются по формулам:

; ; ;

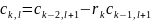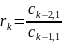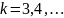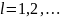
Составим таблицу Рауса для рассматриваемой системы в замкнутом состоянии. Передаточная функция такой системы получена в пункте 1 и имеет следующий вид:

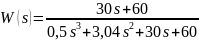
Коэффициенты полинома приведены в таблице 3.

Таблица 3

а0	а1	а2	а3
0,5	3.04	30	60

Найдем значения коэффициентов таблицы Рауса, используя программу на рисунке 11.

Рисунок 11 – Программа для нахождения недостающих коэффициентов таблицы Рауса

В результате работы программы получаем значения, показанные на рисунке 12.

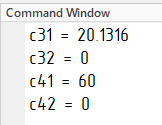
Рисунок 12 – Найденные неизвестные коэффициенты таблицы Рауса

Заполним таблицу Рауса (таблица 4) согласно рисунку 10, используя найденные коэффициенты полинома (рисунок 12):

Таблица 4

№	1	2	3
1	0,5	30	0
2	3,04	60	0
3	20,1316	0	0
4	60	0	0

Согласно критерию Рауса, чтобы система была устойчива, необходимо и достаточно, чтобы все элементы первого столбца таблицы Рауса были положительны. В данном случае, критерий Рауса выполняется, поэтому система является устойчивой.

3.3 Критерий Михайлова

Определим устойчивость замкнутой системы с использованием критерия Михайлова. Запишем ещё раз передаточные функции, полученные в пункте 1.

Передаточная функция замкнутой системы:

Для того чтобы получить кривую Михайлова, используем программу, показанную на рисунке 13:

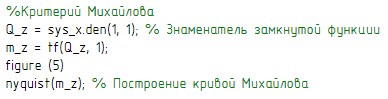
Рисунок 13 – Программа для построения кривой Михайлова

В командном окне получаем следующие значения:

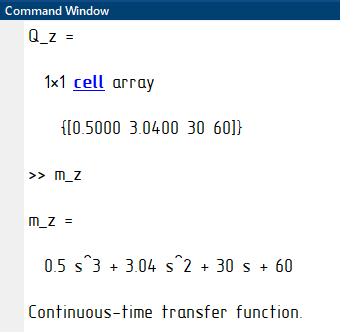
Рисунок 14 – Результат работы программы в MATLAB для построения кривой Михайлова

На рисунке 15 представлена кривая Михайлова для замкнутой системы.

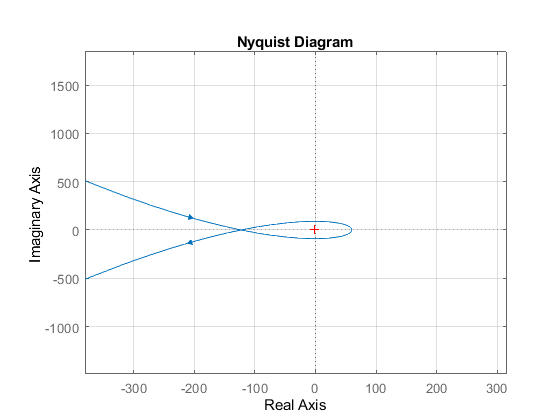
Рисунок 15 – Кривая Михайлова для замкнутой системы

Из рисунка 15 следует, что критерий Михайлова выполняется, так как кривая Михайлова начинается на положительной вещественной полуоси и обходит 3 квадранта на комплексной плоскости против часовой стрелки. Следовательно, замкнутая система устойчива.

3.4 Критерий Найквиста

Согласно критерию устойчивости Найквиста, для того, чтобы замкнутая система управления с отрицательной обратной связью была устойчива, необходимо и достаточно, чтобы разность между положительными и отрицательными переходами АФЧХ замкнутой системы отрезка вещественной оси (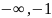 ) была равна 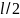(где 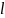– число правых корней характеристического уравнения замкнутой системы). Для построения АФЧХ в MATLAB используется функция nyquist. Чтобы найти корни характеристического уравнения, воспользуемся функцией pole.

Программа для построения АФЧХ системы и для нахождения полюсов передаточной функции приведён на рисунке 16.

Рисунок 16 – Программа для построения АФЧХ и нахождения корней

А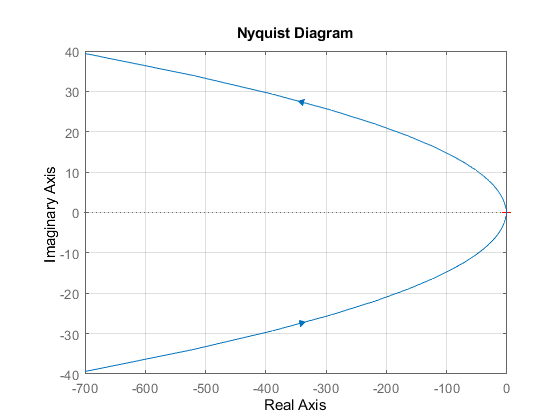 ФЧХ разомкнутой системы приведена на рисунке 17, АФЧХ замкнутой системы – на рисунке 18.

Рисунок 17 – АФЧХ разомкнутой системы

Рисунок 18 – АФЧХ замкнутой системы

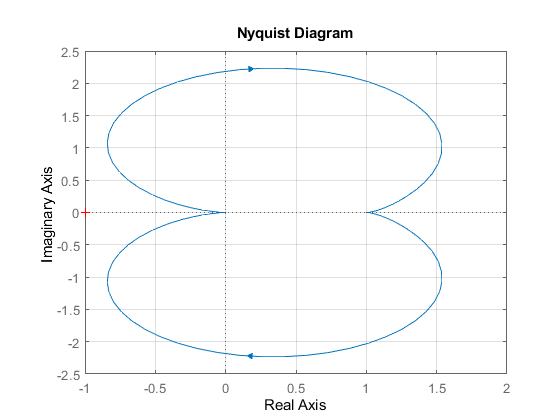
З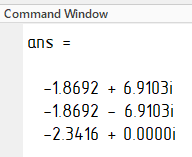 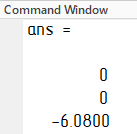начения корней характеристического полинома для разомкнутой системы (слева) и замкнутой системы (справа) представлены на рисунке 19.

Рисунок 19 - Корни характеристического полинома

Так как вещественные части всех корней отрицательные, то число правых корней равно нулю 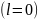. На отрезке ( ) нет ни положительных, ни отрицательных переходов. Следовательно, согласно критерию Найквиста и разомкнутая, и замкнутая система является устойчивой.

Вывод

В ходе выполнения домашнего задания были найдены передаточные функции для заданной системы с разомкнутой и замкнутой обратной связью, были получены графики ЛАЧХ и ЛФЧХ, а также переходной и импульсной переходной характеристик. Также для исходной системы было определено, что система является устойчивой по всем рассмотренным критериям: Гурвица, Рауса, Михайлова и Найквиста.

Список использованной литературы

1. Управление в технических системах: учебник / Н. П. Деменков, Е. А. Микрин. — Москва: Издательство МГТУ им. Н.Э. Баумана, 2017. —452 с.: ил. ISBN 978-5-7038-4661-2. [Электронный источник] (дата обращения 17.11.2023 г.) Ссылка: https://bmstu.press/catalog/item/5057/

2. Ким Д. П. Теория автоматического управления. Т. 1. Линейные системы — 2-е изд., испр. и доп. — М.: ФИЗМАТЛИТ, 2016. — 312 с.

3. Ким  Д. П. Теория автоматического управления. Т. 2. Многомерные, нелинейные, оптимальные и адаптивные системы — 2-е изд., испр. и доп. — М.: ФИЗМАТЛИТ, 2016. — 440 с.