Министерство цифрового развития и массовых коммуникаций

Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение

высшего образования

«Московский технический университет связи и информатики»

(МТУСИ)

Кафедра Теории электрических цепей

Отчет по лабораторной работе №14

по дисциплине «Электротехника»

на тему:

«Исследование КИХ-фильтров»

Выполнила: студент группы .

.

Проверил:

Волков Алексей Станиславович

Москва 2023

Содержание

1. Цель работы

С помощью программы Micro-Cap получить основные временные и частотные характеристики фильтров с конечной импульсной характеристикой (КИХ-фильтров).

2.Предварительные расчеты

1. Найти передаточную функцию H(z) трехзвенного КИХ-фильтра второго

порядка, выполняющего функцию скользящего среднего.

Где

y_i = a₀x_i + a₁x_i-1 + a₂x_i-2 — алгоритм работы цифрового фильтра;

a₀ = a₁ = a₂ = 1/3 — коэффициенты.

Передаточная функция КИХ-фильтра H(z):

H(z) = a₀ + a₁z^-1 + a₂z^-2 + … + a_N-1z^-(N-1) = (1 + z^-1 + z^-2)

2.2 Найти выражение для комплексного коэффициента передачи H(jωT). Построить графики АЧХ — |H(jωT)| и ФЧХ — arg(H(jωT)) от частоты ωT ϵ [0;2π] (T=const — интервал дискретизации по времени) данного фильтра.

Для получения дальнейших характеристик проведем замену в H(z): z = e^jωT

Частотный коэффициент передачи

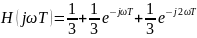
АЧХ:

ФЧХ:

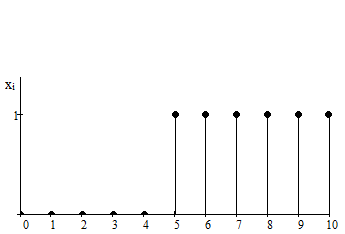
2.3 Получить реакцию данного КИХ-фильтра на ступенчатое воздействие. Построить график y_i. Получить импульсную характеристику данного фильтра и построить её график.

График y_i:

Импульсная характеристика будет иметь вид:

Определяется из коэффициентов передаточной функции H(z)

График импульсной характеристики g(iT):

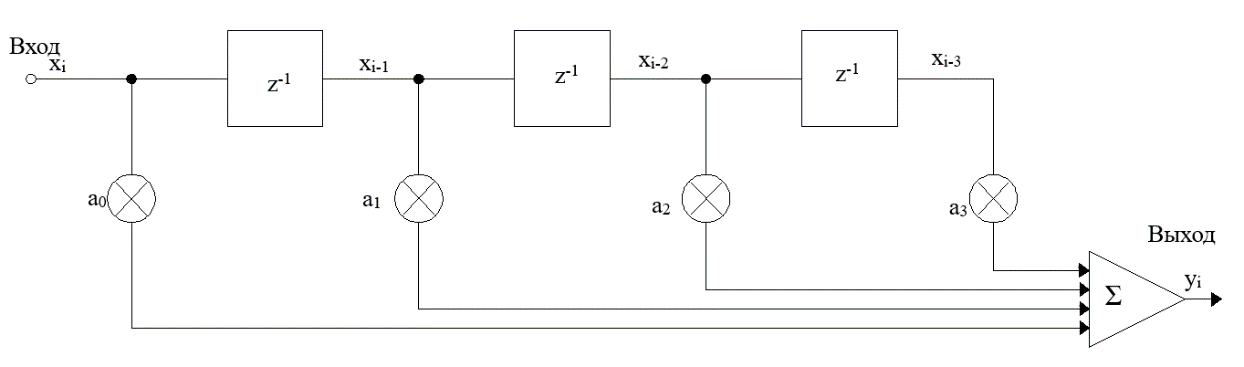2.4 Нарисовать структурную схему четырехзвенного КИХ-фильтра, выполняющего функцию скользящего среднего. Найти его передаточную функцию H(z). Построить графики АЧХ и ФЧХ данного фильтра.

Передаточная функция H(z):

H(z) = a₀ + a₁z^-1 + a₂z^-2 + … + a_N-1z^-(N-1) = (1 + z^-1 + z^-2 + z^-3)

АЧХ:

ФЧХ:

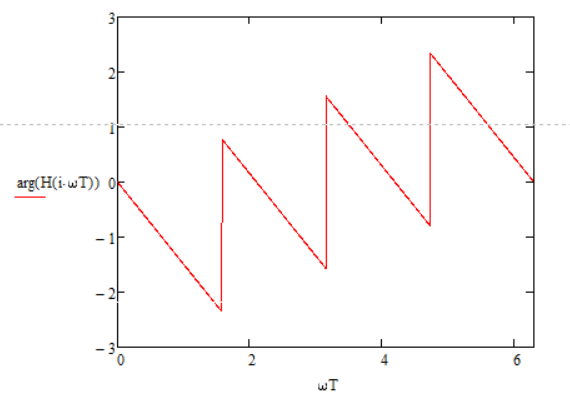
2.5 Нарисовать структурную схему пятизвенного КИХ-фильтра, выполняющего функцию скользящего среднего. Найти его передаточную функцию H(z). Построить графики АЧХ и ФЧХ данного фильтра.

Передаточная функция H(z):

H(z) = a₀ + a₁z^-1 + a₂z^-2 + … + a_N-1z^-(N-1) = (1 + z^-1 + z^-2 + z^-3 + z^-4)

АЧХ:

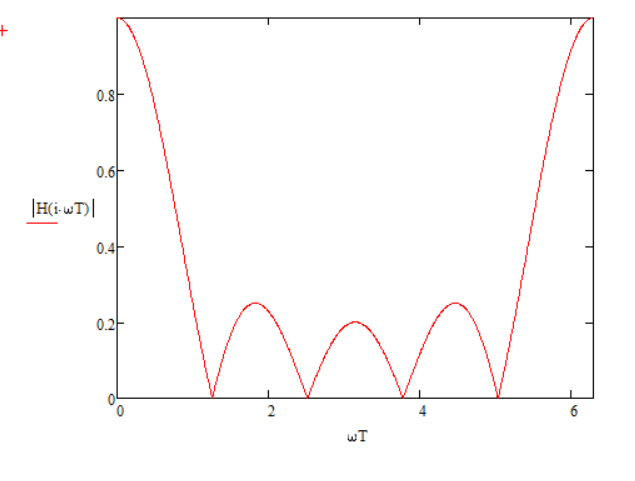
ФЧХ:

3. Обработка результатов машинного эксперимента

Схема в Micro-Cap:

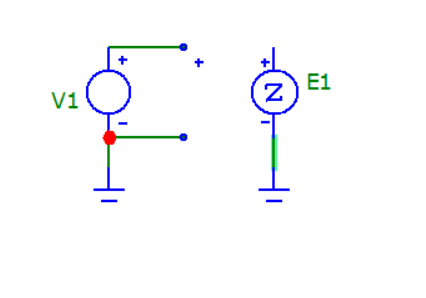
АЧХ трёхзвенного КИХ-фильтра:

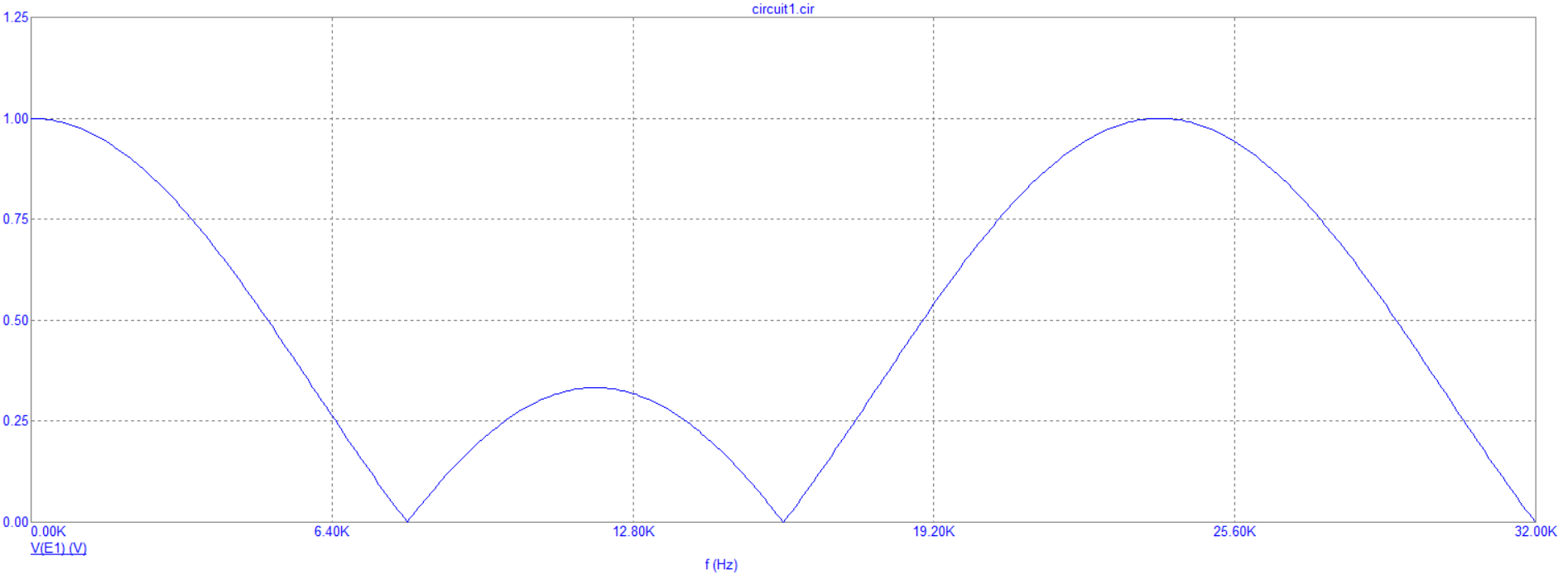
АЧХ четырёхзвенного КИХ-фильтра:

АЧХ пятизвенного КИХ-фильтра:

Вывод:

Получены передаточные функции, частотные характеристики и графики АЧХ и ФЧХ КИХ – фильтров второго, третьего и четвертого порядков. Результаты предварительного расчета совпали с результатами компьютерного моделирования.

Контрольные вопросы:

1.Что называется z-преобразованием?

Ответ: Пусть {x(k)}=(x₀, x₁, x₂, …) — числовая последовательность, конечная или бесконечная, содержащая отсчеты некоторого сигнала, тогда односторонним z-преобразованием этой последовательности называется сумма

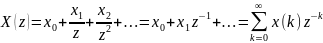
2.Какими свойствами обладает z-преобразование?

Ответ: 1) Линейность

2) Свойство задержки

3) Теорема свертки

3.Какие фильтры называются цифровыми?

Ответ: Цифровым фильтром называется цифровая система, которую можно использовать для фильтрации дискретных сигналов.

4.Дать определение передаточной функции цифрового фильтра.

Ответ: Передаточной функцией стандартного линейного ЦФ называется отношение z-преобразования выходного сигнала к z-преобразованию входного сигнала.

5.Какие фильтры называются КИХ-фильтрами?

Ответ: Фильтром с конечной импульсной характеристикой (КИХ-фильтром) называют фильтр, у которого импульсная представляет собой конечную дискретную последовательность, т.е. принимает отличные от нуля значения при k = 0, 1, …, m.