4.2 Многофакторный регрессионный анализ

Вводим исходные данные:

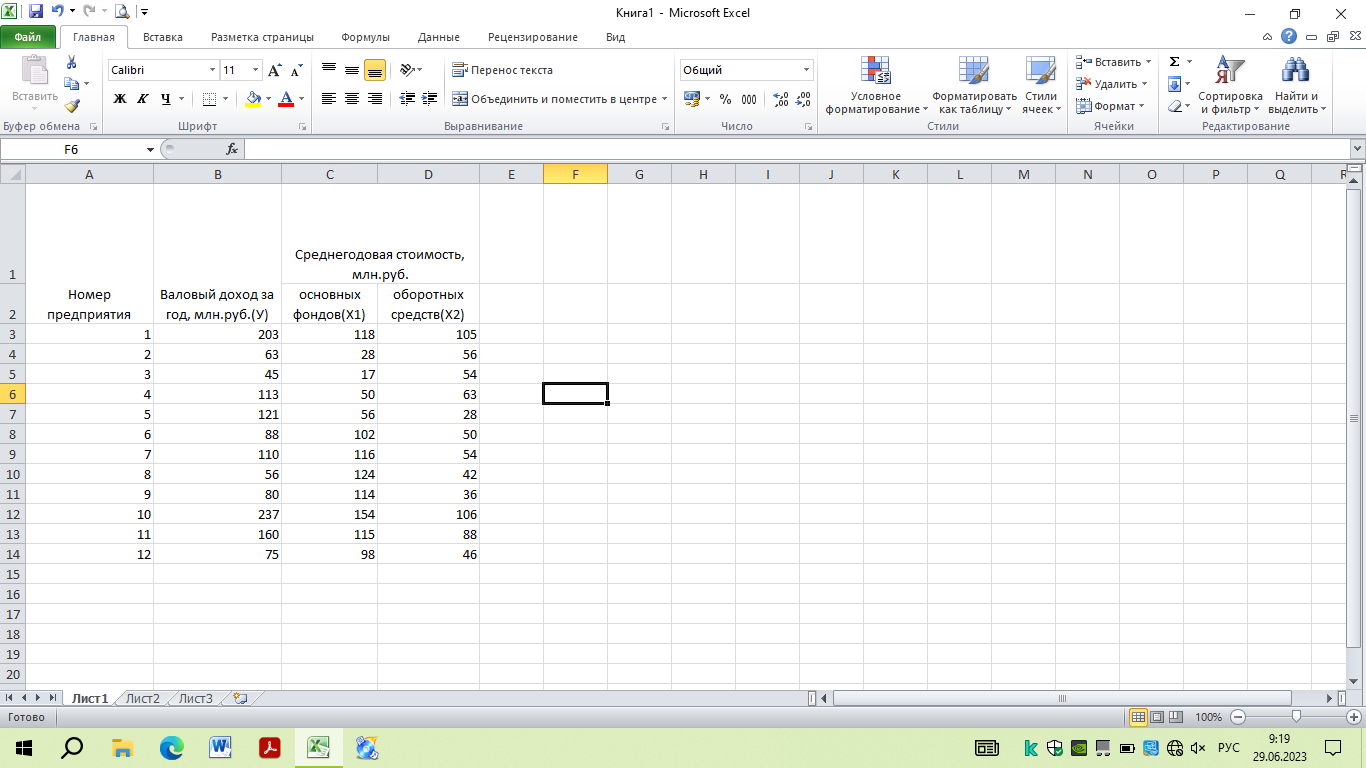
Рисунок 48 – Исходные данные

Решение:

1. Построим линейное уравнение множественной регрессии и поясним экономический смысл его параметров.

Линейное уравнение множественной регрессии у от х₁ х₂ имеет вид:

y=b₀+b₁x₁+b₂x₂

Определим коэффициенты уравнения регрессии

Рисунок 49 – Окно регрессии

Представлены результаты расчетов:

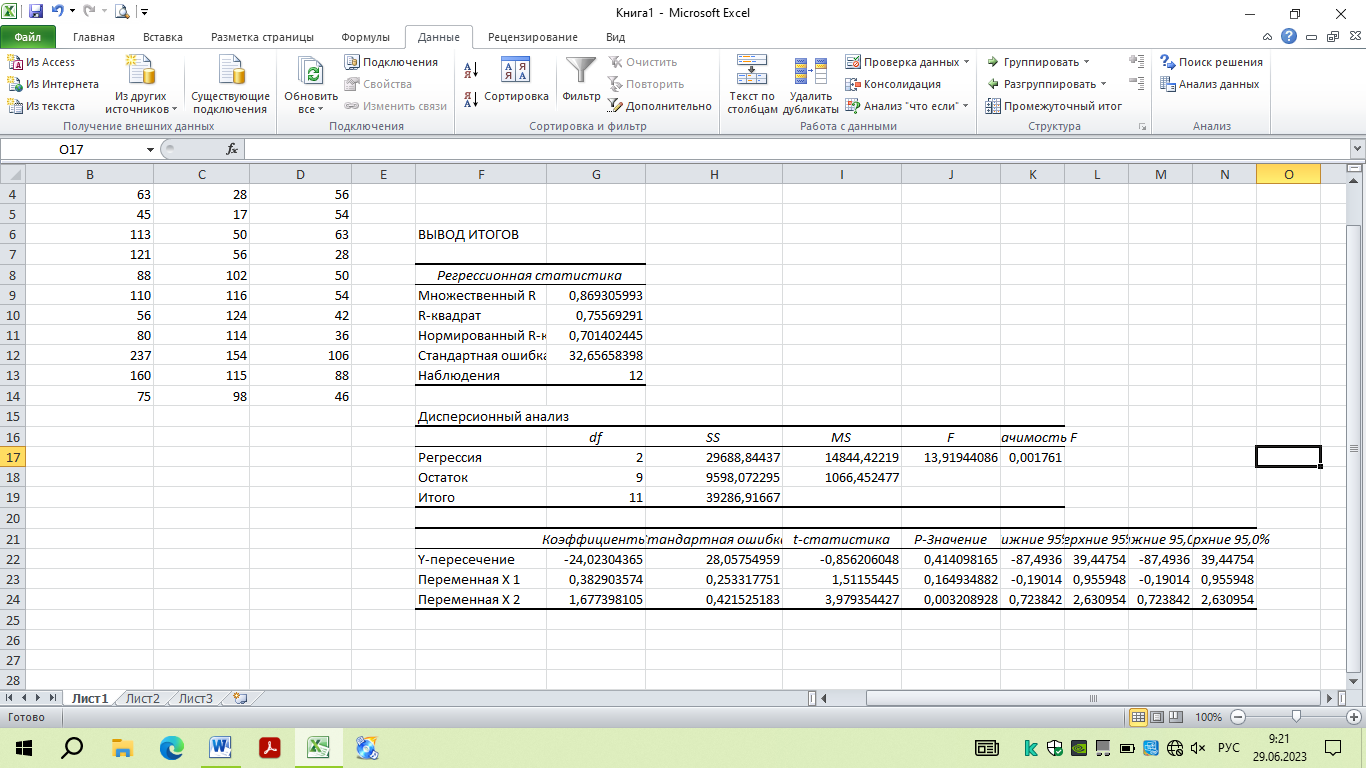
Рисунок 50 – Результат регрессии

Уравнение регрессии: Y= -24,023 + 0,383 Х1 + 1,677 Х2

2. Определим стандартизованные коэффициенты регрессии.

Проведем корреляционный анализ данных:

Рисунок 51 – Окно корреляции

Представлены результаты расчетов:

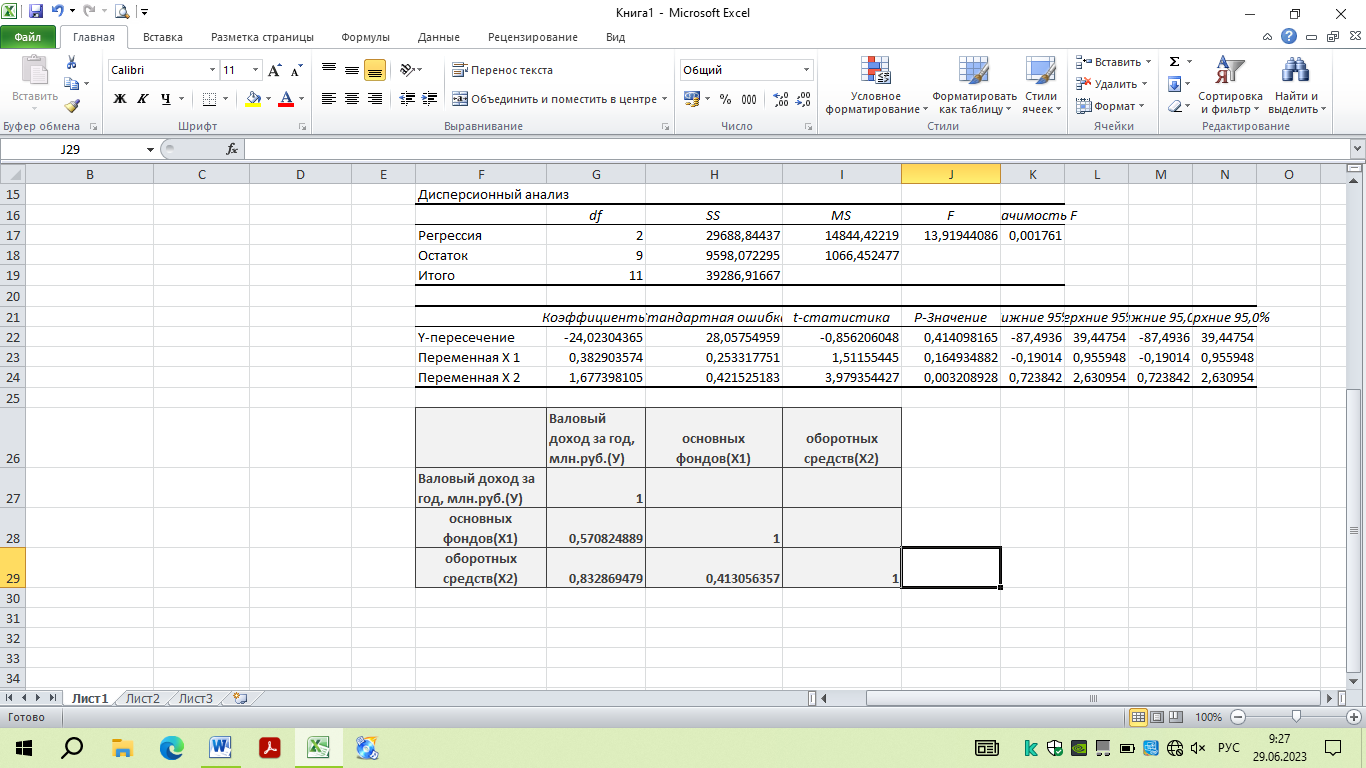
Рисунок 52 – Результат корреляции

Для оценки ẞ-коэффициентов применим МНК. При этом система нормальных уравнений будет иметь вид:

r_x1y= ẞ₁+r_x1x2* ẞ+…+r_x1xm* ẞ_m

r_x2y=r_x2x1* ẞ₁+ ẞ₂+…+r_x2xm* ẞ_m

r_xmy=r_xmx1* ẞ₂+r_xmx2* ẞ₂+…+ ẞ

Для наших данных (берем из матрицы парных коэффициентов корреляции):

0, 571= ẞ₁+0,413 ẞ₂

0,833= 0,413 ẞ₁₊ ẞ

Искомое уравнение в стандартизованном масштабе t_y= ẞ₁t_x1+ ẞ₂t_x2

Расчет ẞ-коэффициентов можно выполнить и по формулам:

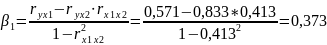
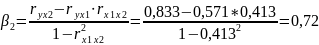
Стандартизированная форма уравнения регрессии имеет вид:

t_y = 0,273 х₁+0,72х₂

3. Определим парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции, сделать вывод.

Коэффициент множественной корреляции можно определить через матрицы парных коэффициентов корреляции:

где

– определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.

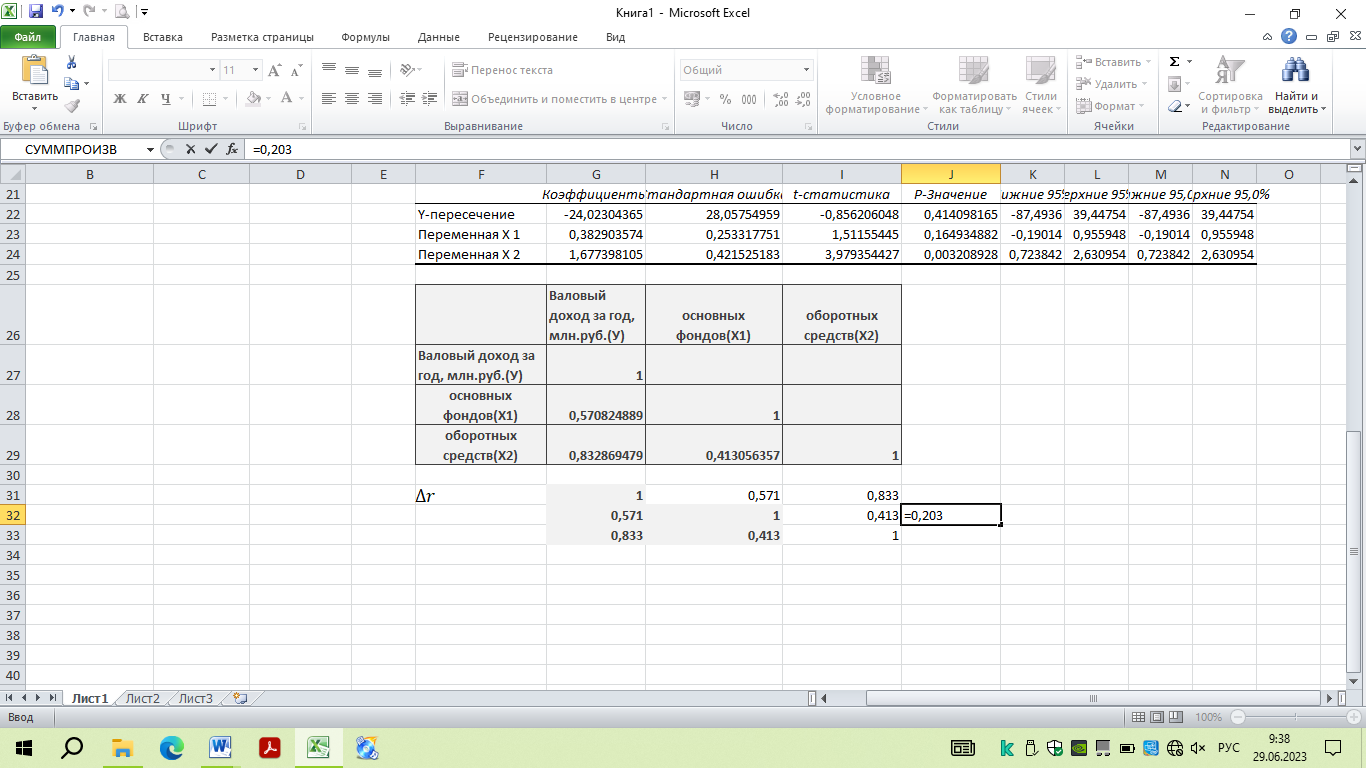
Рисунок 53 – Определение коэффициента множественной корреляции через матрицы парных коэффициентов корреляции

Коэффициент множественной корреляции

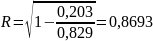
Связь между признаком Y и факторами Х₁ низкая.

Расчет коэффициента корреляции выполним, используя известные значения линейных коэффициентов парной корреляции и -коэффициентов.

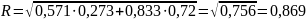
Коэффициент детерминации

R² = 0,756

Частные коэффициенты корреляции.

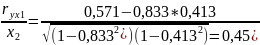
Теснота связи не сильная

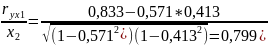
Теснота связи сильная

=

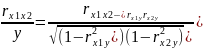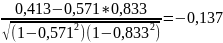
Теснота связи низкая. Межфакторная связь слабая.

4. Дать оценку полученного уравнения на основе коэффициента детерминации и общего F-критерия Фишера.

Теснота связи результативного признака с факторными определяется величиной коэффициента линейной множественной корреляции и детерминации, который могут быть исчислены на основе матрицы парных коэффициентов корреляции:

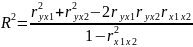
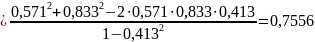
Проверка гипотезы H₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R² = 0) производится по F-критерию Фишера сравнением F_факт с F_табл.

Если расчетное значение с k1= (m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

R= 0, 7556

Выдвигаем нулевую гипотезу о том, что уравнение в целом статистически незначимо: H₀: R²= 0 на уровне значимости

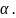
Определяют фактическое значение F-критерия:

F= * = 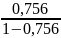* 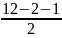= 13,92

где m=2 для множественной регрессии с двумя факторами.

Табличное значение критерия со степенями свободы k1=2 и k2=9, F_KP=4,26.

Поскольку фактическое значение F>F_kp, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).