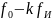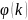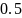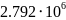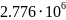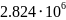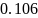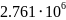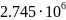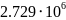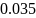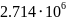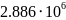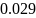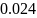- •Федеральное агентство связи
- •Московский технический университет связи и информатики
- •Техническое задание.
- •Исходные данные.
- •Временные диаграммы
- •По заданной функции корреляции исходного сообщения:
- •Рассчитать интервал корреляции, спектр плотности мощности, начальную энергетическую ширину спектра сообщения.
- •Построить в масштабе графики функций корреляции и спектра плотности мощности. Отметить на них найденные в пункте 2.1. Параметры:
- •Рассчитать среднюю квадратичную погрешность фильтрации (скпф) сообщения, среднюю мощность отклика ифнч, частоту и интервал временной дискретизации отклика ифнч:
- •Полагая, что последовательность дискретных отчётов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:
- •Рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратичную погрешность квантования скпк:
- •4.2. Построить в масштабе характеристику квантования
- •Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе l-ичного дискретного канала связи (дкс):
- •Рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность l-ичного дискретного источника
- •Построить в масштабе графики рассчитанных закона и функции распределения вероятностей.
- •Закодировать значения l-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода
- •Рассчитать априорные вероятности передачи по двоичному дкс символов нуля и единицы, начальную ширину спектра сигнала икм
- •Полагая, что для передачи икм сигнала по непрерывному каналу связи (нкс) используется гармонический переносчик:
- •Рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра:
- •Построить в масштабе четыре графика функции плотности вероятностей (фпв) мгновенных значений и огибающих узкополосной гауссовской помехи (угп) и суммы гармонического сигнала с угп.
- •С учётом заданного вида приёма (детектирования) сигнала дискретной модуляции:
- •Рассчитать среднюю вероятность ошибки в двоичном дкс, скорость передачи информации по двоичному симметричному дкс, показатель эффективности передачи сигнала дискретной модуляции по нкс.
- •Изобразить схему приёмника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи когда он выносит ошибочные решения.
- •Рассматривая отклик детектора пру как случайный дискретный сигнал на выходе l-ичного дкс:
- •Полагая фнч на выходе цап приемника идеальным с полосой пропускания равной начальной энергетической ширине спектра исходного сообщения:
Рассчитать априорные вероятности передачи по двоичному дкс символов нуля и единицы, начальную ширину спектра сигнала икм
Так
как среднее число нулей
![]() и среднее число единиц
и среднее число единиц
![]() в сигнале ИКМ одинаково, то и вероятности
их появления одинаковы: p(0)=p(1)=0.5
в сигнале ИКМ одинаково, то и вероятности
их появления одинаковы: p(0)=p(1)=0.5
Ширина спектра сигнала ИКМ
![]()
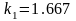 - постоянная
- постоянная
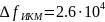 Гц
Гц
Полагая, что для передачи икм сигнала по непрерывному каналу связи (нкс) используется гармонический переносчик:
Рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра:
Сигнал ДАМ представляется в виде:
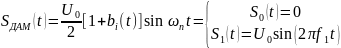
Разложение сигнала по гармоническим составляющим имеет следующий вид:

Спектр гармонического сигнала имеет только нечетные гармонические составляющие на частотах
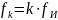 ,
k=1,3,5…
,
k=1,3,5…
При неизвестной амплитуде U0 вычисляют нормированный спектр
Uk/U0=φ(f)
Ширина спектра сигнала ДАМ равна:
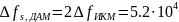 Гц
Гц
7.2. Построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нём найденную ширину спектра.


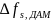
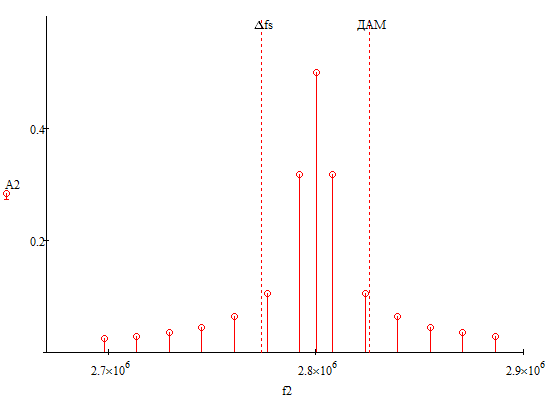
Рис. 16. Нормированный спектр сигнала дискретной модуляции
Таблица 8.
|
|
|
|
0 |
|
|
|
1 |
|
|
|
3 |
|
|
|
5 |
|
|
|
7 |
|
|
|
9 |
|
|
|
11 |
|
|
|
13 |
|
|
|
Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции и заданными спектральной плотностью мощности помехи и отношением сигнал-шум:
Рассчитать приходящееся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС.
Мощность
гауссовского белого шума
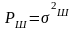 геометрически определяется как площадь
прямоугольника с высотой
геометрически определяется как площадь
прямоугольника с высотой
 и основанием
и основанием
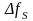 :
:
 Вт
Вт
где - ширина спектра сигнала ДАМ.
Учитывая то, что начальное соотношение сигнал-шум (ОСШ)
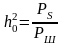 на
входе детектора приемника известно,
находим мощность сигнала дискретной
модуляции, обеспечивающей это ОСШ:
на
входе детектора приемника известно,
находим мощность сигнала дискретной
модуляции, обеспечивающей это ОСШ:
 Вт
Вт
Рассчитаем приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала:
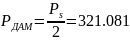 Вт
Вт
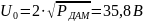
Пропускная способность НКС характеризует максимально возможную скорость передачи информации по данному каналу. Она определяется:
 дв.ед/с
дв.ед/с
Построить в масштабе четыре графика функции плотности вероятностей (фпв) мгновенных значений и огибающих узкополосной гауссовской помехи (угп) и суммы гармонического сигнала с угп.
ФПВ мгновенных
значений УГП имеют вид гауссовского
распределения (рис.17) с числовыми
характеристиками
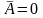 - математическое ожидание,
- математическое ожидание,
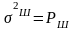 - мощность.
- мощность.
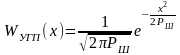 ;
;
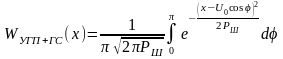
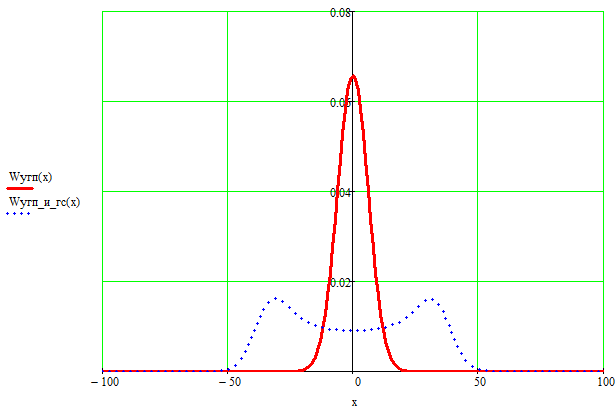
Рис. 17. Функции плотности вероятностей (ФПВ) мгновенных значений
Огибающая гауссовской помехи распределена по закону Рэлея:

Огибающая принимаемой суммы гармонического сигнала + УГП подчиняется обобщенному распределению Рэлея :
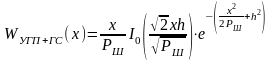 ,
,
где
 - модифицированная функция Бесселя
нулевого порядка от мнимого аргумента.
- модифицированная функция Бесселя
нулевого порядка от мнимого аргумента.

Рис. 18. Огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП.