Наглядный пример Пример 1
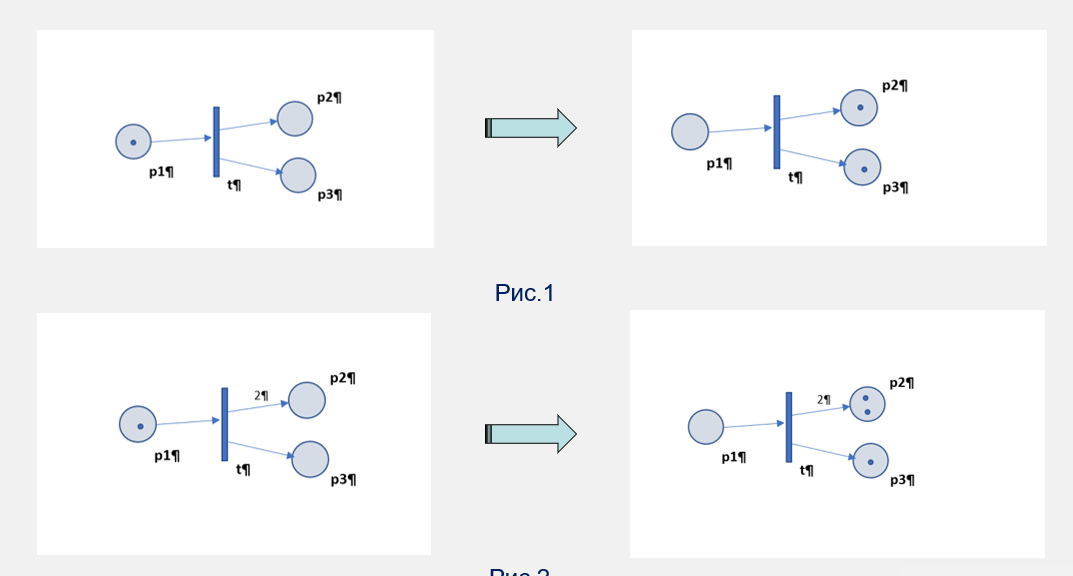
Если из перехода идет несколько связей, то метка “разделяется” на все позиции, соединенные с этим переходом. Поэтому в 1 ситуации обе позиции после перехода имеют метки.
во 2 случае в верхнюю позицию пошло 2 метки так как вес у верхней стрелки - 2, а у нижней - 1
Пример 2
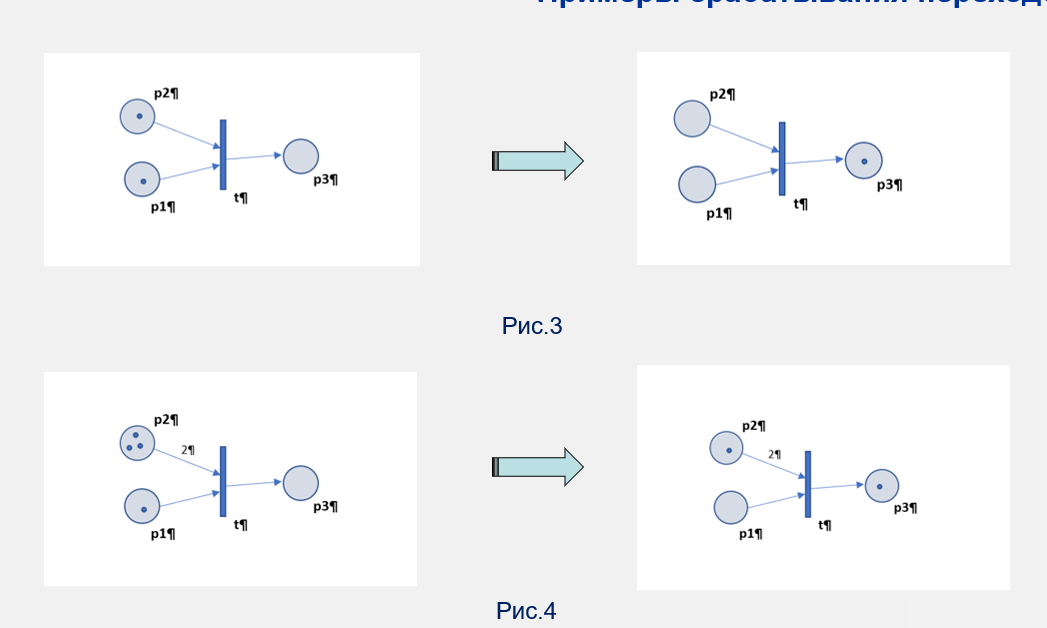
Если в переход идет несколько связей, то необходимо, чтобы в позициях до перехода было достаточно меток для выполнения этого перехода. Если у связи нет явно заданного веса (рисунок 3), то подразумевается, что достаточно по 1 метке в позициях. если же вес указан явно (рисунок 4), то необходимо столько меток в позиции, сколько вес у связи.
Для 2 случая: из 3х меток осталась одна в левой верхней позиции так как у стрелки, идущей в переход из этой позиции, вес равен 2
Пример 3
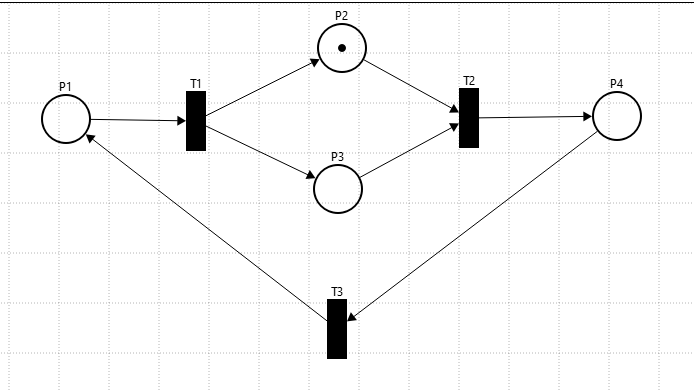
Это пример тупиковой разметки, так как для срабатывания перехода T2 необходимо, чтобы метки находились в позициях P2 и P3, но в P3 нет метки, поэтому дальнейшее функционирование системы невозможно
Пример 4
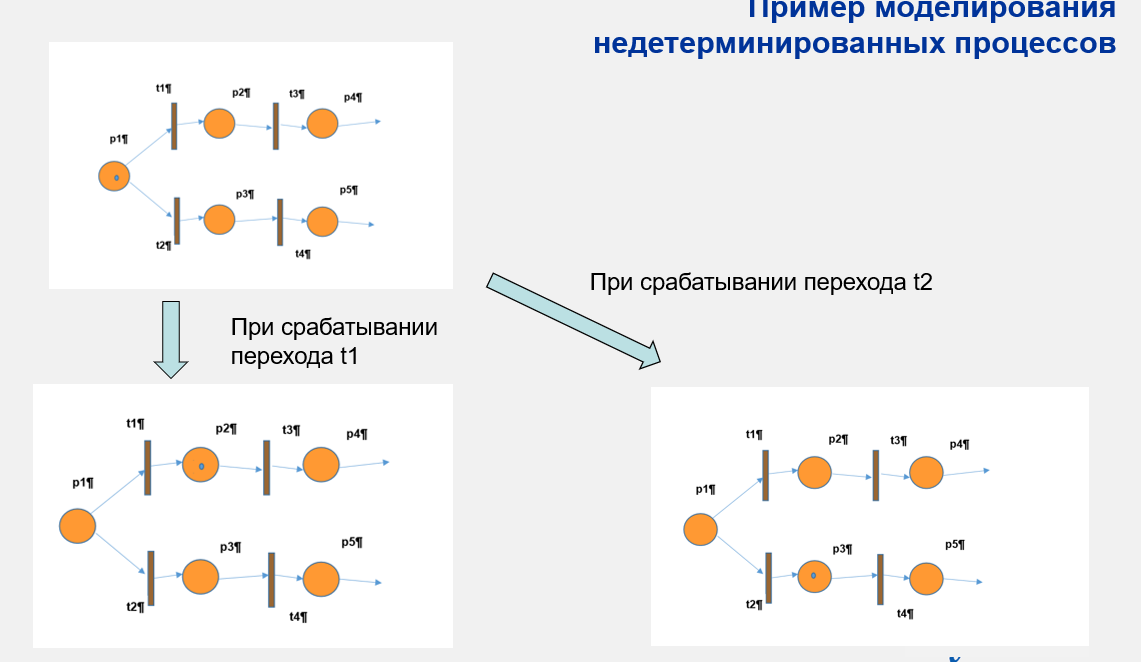
Если из позиции связи идут в несколько переходов, то следующую разметку можно получить активацией любого перехода
Сети Петри: дерево достижимых разметок.
теория
Пример
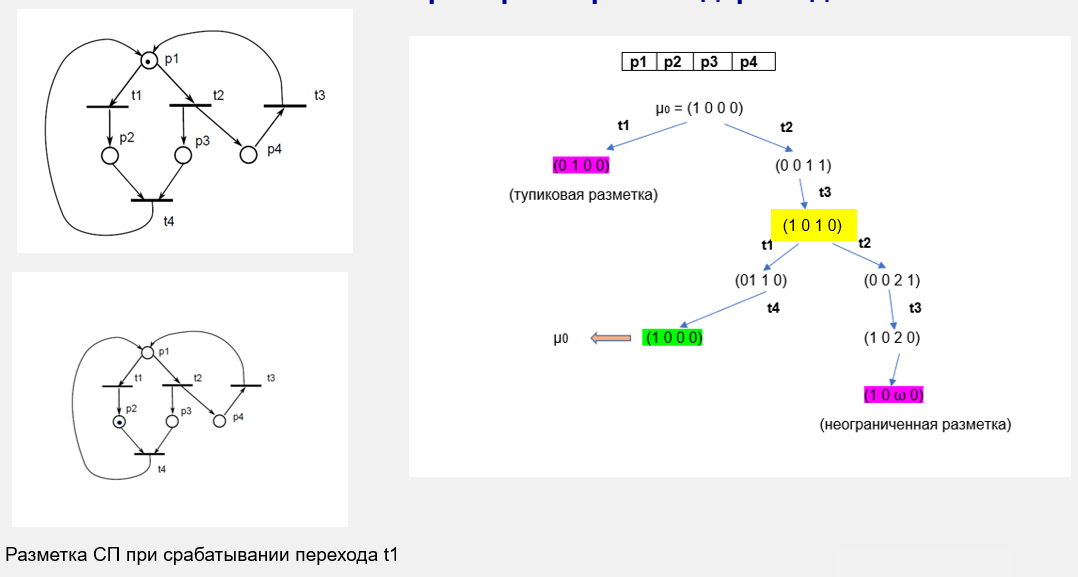
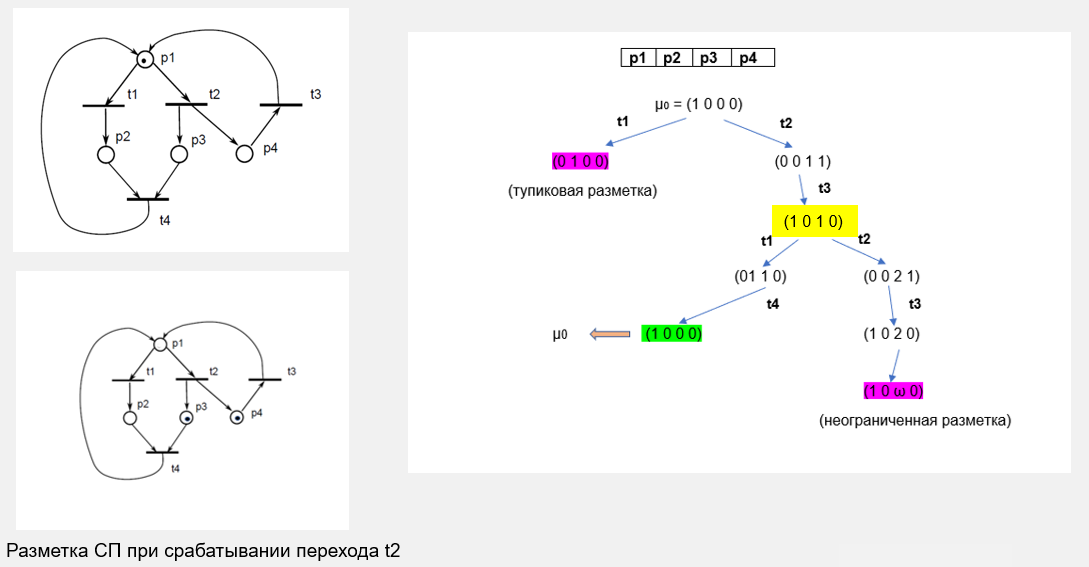
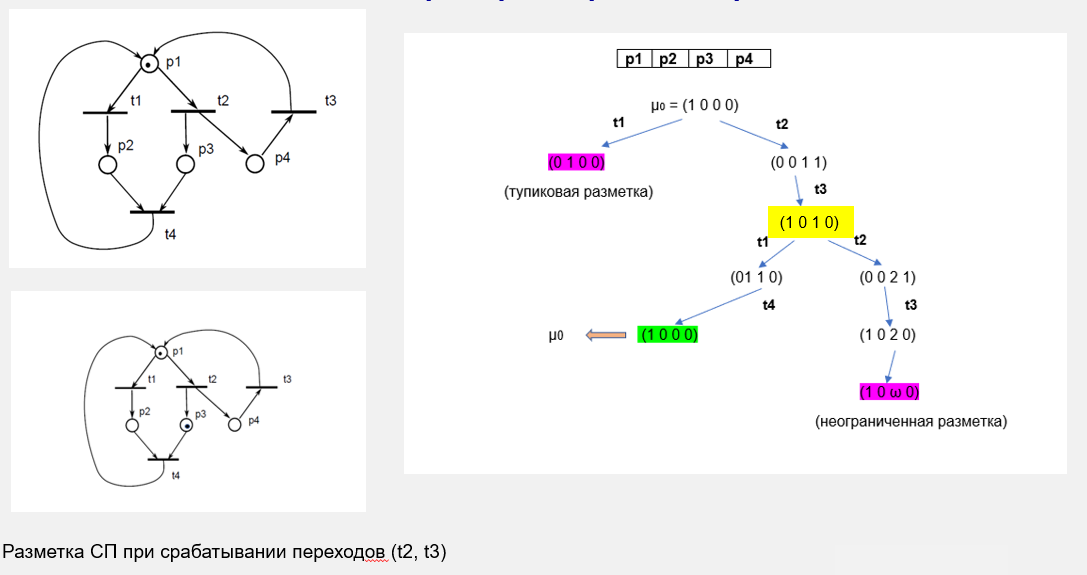
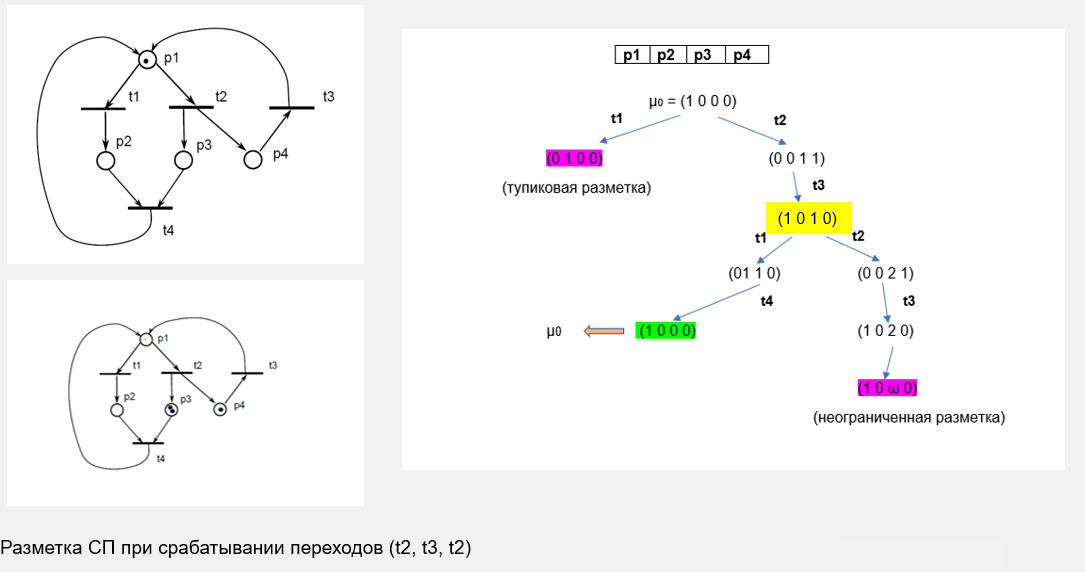
Оценка свойств сетей Петри на основе матричных уравнений.
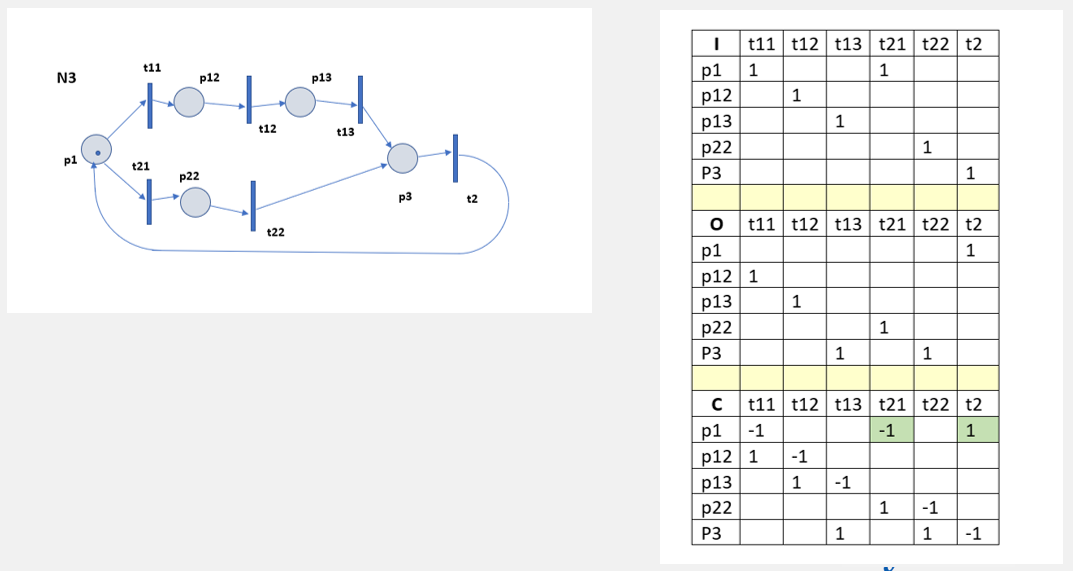
Теория
Показано, что если СП живая и ограниченная, то она должна быть последовательной и инвариантной. Данные свойства недостаточны для утверждения живости и ограниченности СП. Однако их полезно проверить исходя из матриц инцидентности, так как если одно из этих свойств не подтверждается, то можно заключить, что описываемая система содержит некоторые недоработки.
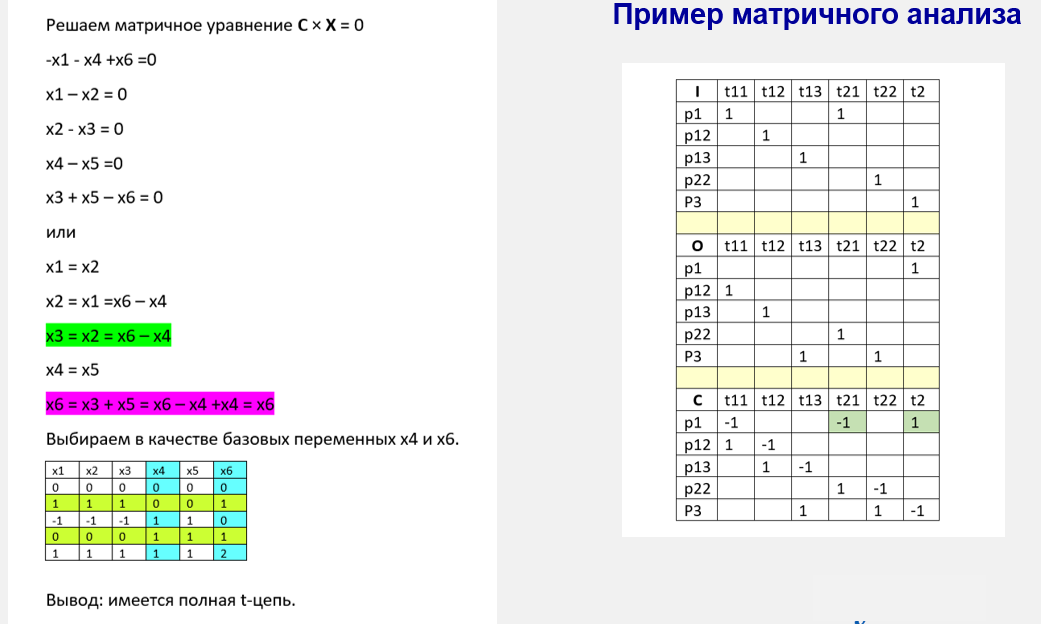
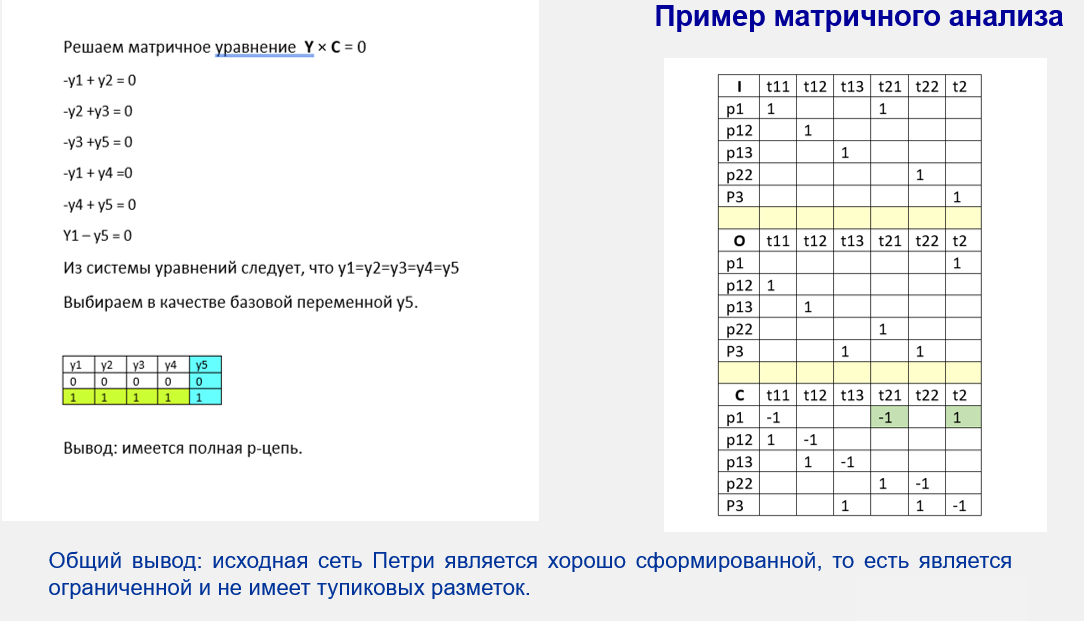
Пример
Алгебра сетей Петри: операции над сетями Петри.
Операции над сетями Петри позволяют комбинировать, преобразовывать и анализировать системы для понимания их поведения.
Объединение (Union): Объединение двух сетей Петри создает новую сеть, содержащую все места, переходы и их связи из обеих сетей. Места и переходы из разных сетей считаются различными, даже если они имеют одинаковые имена.
Параллельное соединение (Parallel Composition): Параллельное соединение двух сетей Петри объединяет их таким образом, что каждая сеть может быть рассмотрена как отдельный компонент. Все места одной сети соединяются с соответствующими местами другой сети, образуя новый набор мест. Переходы также объединяются, и каждый переход одной сети соединяется с соответствующим переходом другой сети.
Инкремент (Increment): Инкремент создает новую сеть Петри путем добавления одного или нескольких дополнительных меток к каждому месту исходной сети. Метки могут быть добавлены к любому месту или всем местам одновременно. Это часто используется для моделирования начальных условий системы.
Декремент (Decrement): Декремент выполняется аналогично инкременту, но вместо добавления меток, метки удаляются.
Расширения сетей Петри: ингибиторные, приоритетные, временные.
Ингибиторные
В рассмотренных СП недостатком является то, что нельзя отметить срабатыванием перехода факт изменения разметки с ненулевого значения на нулевое. Таким образом из двух альтернатив
(p) 0 и (p) = 0, содержащихся в операторе условного вычитания единицы, в СП можно представить только одну, первую, но нельзя отразить проверку на ноль, так как сеть не может реагировать непосредственно на отсутствие метки в позиции. В результате было показано, что СП не могут моделировать машины Минского и Тьюринга.
Флинн и Аджервала модифицировали СП, введя в них специальные ингибиторные дуги, осуществляющие проверку на нулевую разметку, и показали, что получаемое обобщение дает класс сетей равномощных машине Тьюринга.
Приоритетные
Временные
