Модели представления знаний. Продукционные и фреймовые модели.
Продукционная форма используется для представления знаний в виде импликативных отношений и связок («и») и («или») между фактами. Продукционная форма широко используется в системах продукций, которые являются основой экспертных систем для консультаций, диагностики, поддержки принятия решений и управления.
Фреймовая форма соответствует фреймовой сети и является мощным средством построения больших иерархических систем для представления и обработки изображений, речевых образов, процессов управления, диагностирования и пр. Для поддержки разработки фреймовых систем используются специализированные программные средства. Фреймовые сети в настоящее время развиваются в сторону универсализации, т. е. фреймы трансформируются в более универсальные объекты с полным набором свойств объектно-ориентированного программирования. Такой подход часто используется в разработках мощных распределенных сетевых систем знаний для моделирования, управления, проектирования и пр. Универсальный вариант объектной модели знаний поддерживается средствами объектно-ориентированного проектирования баз знаний.
Методы работы со знаниями. Механизм вывода решений
Экспертные системы. Структура экспертных систем.
Экспертные системы. Классификация экспертных систем.
Экспертные системы. Этапы разработки экспертных систем.
Инструментальные средства создания интеллектуальных систем. Решающие деревья.
Сетевые модели. Сети Петри. Основные понятия и определения.
Сети Петри: формы представления сетей Петри, графы сетей Петри, правила функционирования сетей Петри.
Формы представления сетей Петри:
графический (отображаются позиции, переходы и их связи в виде ориентированного графа):
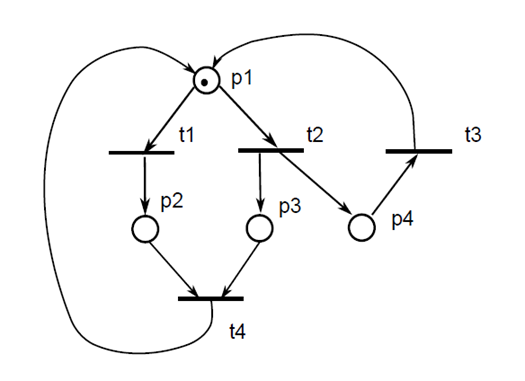
матричный (позиции, переходы и их связи отображаются в виде матриц I (связь позиций с переходами - в какие переходы можно попасть из конкретной позиции), O (связь переходов с позициями - в какие позиции можно попасть из конкретного перехода) и μ0 (начальное состояние системы - показывает, в каких позициях присутствуют метки))
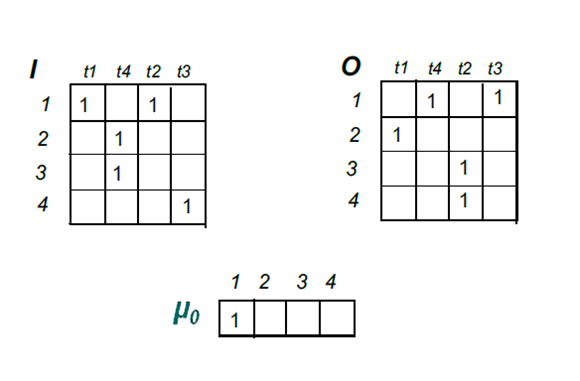
Графы сетей Петри Скучная и непонятная теория из лекций
Сеть Петри (СП) - это двудольный ориентированный мультиграф N = (P, T, I, O, µ0), где:
P - конечное непустое множество элементов, называемых позициями; T - конечное непустое множество элементов, называемых переходами; I: PT{0,1,2...} и O: PT{0,1,2...} - функции инцидентности;
µ0 : P{0,1,2...} - начальная разметка.
n =P- мощность множества P,
m =T - мощность множества T.
СП обычно представляют в виде геометрического объекта. При этом позиции изображают кружками, переходы - черточками или прямоугольниками.
Дуга проводится от позиции pi к переходу tj, если I(pi, tj) > 0, и от перехода tj к позиции pi, если O( pi, tj) > 0.
Правила функционирования сетей Петри
При функционировании СП переходит от одной разметки к другой. Каждая разметка представляет собой функцию : P{0,1,2...}. Переход может сработать при разметке , если он активен.
Переход tj является активным, если pi pre(tj): (pi ) >= I( pi, tj) .
В результате срабатывания перехода tj разметка меняется в соответствии со следующим правилом:
pi (pre( tj) post(tj)) : ‘(pi ) = (pi ) - I(pi, tj) + O( pi, tj) .
В этом случае говорят, что разметка ‘ достижима от разметки в результате срабатывания перехода tj, а разметка предшествует ‘.
СП останавливается, если при некоторой разметке не может сработать ни один из ее переходов. Такая разметка называется тупиковой.