43. Нейронные сети. Представление данных. Примеры.

Данные, которыми придется манипулировать при работе с нейронными сетями, почти всегда будут относиться к одной из таких категорий, как:

векторные данные — двумерные тензоры с формой (образцы, признаки), где каждый образец — это вектор числовых атрибутов («признаков»);

временные ряды или последовательности — трехмерные тензоры с формой (образцы, метки_времени, признаки), где каждый образец является последовательностью (длиной метки_времени) векторов признаков;

изображения — четырехмерные тензоры с формой (образцы, высота, ширина, цвет), где каждый образец является двумерной матрицей пикселей, а каждый пиксель представлен вектором со значениями «цвета»;

видео — пятимерные тензоры с формой (образцы, кадры, высота, ширина, цвет), где каждый образец является последовательностью (длина равна значению кадры) изображений.

Видеоданные — один из немногих типов данных, для хранения которых требуются пятимерные тензоры. Видео можно представить как последовательность кадров, где каждый кадр — цветное изображение. Каждый кадр можно сохранить в трехмерном тензоре (высота, ширина, цвет), соответственно, их последовательность можно поместить в четырехмерном тензоре (кадры, высота, ширина, цвет), а пакет разных видеороликов — в пятимерном тензоре с формой (образцы, кадры, высота, ширина, цвет).

Например, 60-секундный видеоклип с разрешением 144 × 256 и частотой четыре кадра в секунду будет состоять из 240 кадров. Для сохранения пакета из четырех таких клипов потребуется тензор с формой (4, 240, 144, 256, 3). То есть 106 168 320 значений! Если предположить, что dtype тензора определен как float32, тогда для хранения каждого значения понадобится 32 бита, а для всего тензора соответственно 405 Мбайт.

44. Нейронные сети. Операции с тензорами. Примеры.

Пусть имеется следующий вектор: A = [0.5, 1],

он определяет направление в двумерном пространстве. Добавим новый вектор

B = [1, 0.25] и сложим его с предыдущим.

Чтобы получить результирующий вектор, представляющий сумму двух исходных векторов, достаточно перенести начало одного вектора в конец другого. Операция прибавления вектора B к вектору A заключается в переносе точки A в новое место, при этом расстояние и направление переноса от исходной точки A определяется вектором B. Если применить ту же операцию к группе точек на плоскости («объекту»), можно создать копию целого объекта в новом месте. То есть тензорное сложение представляет операцию параллельного переноса объекта (без его искажения) на определенное расстояние в определенном направлении.

Элементарные геометрические операции, такие как параллельный перенос, поворот, масштабирование, наклон и т. д., можно выразить в виде операций с тензорами.

Параллельный перенос: добавление вектора к точке переместит ее на фиксированное расстояние в фиксированном направлении; при применении к набору точек (например, к двумерному объекту) эта операция называется параллельным переносом.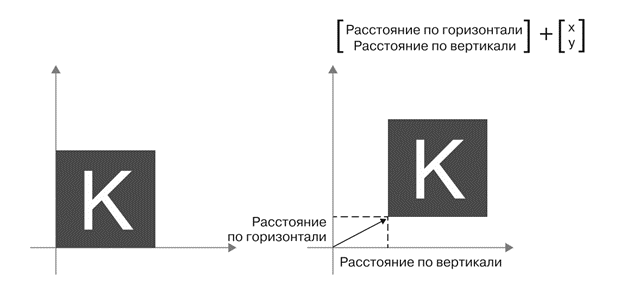

Поворот: поворот двумерного вектора на угол α выражается как скалярное произведение с матрицей R = [u, v] размером 2 × 2.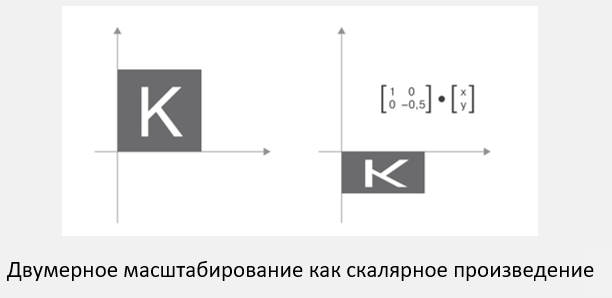

Масштабирование: масштабирование изображения по вертикали и горизонтали (слайд) можно осуществить с помощью скалярного произведения с матрицей 2 × 2:

S = [[масштаб_по_горизонтали, 0], [0, масштаб_по_вертикали]]

Такие матрицы называются диагональными, поскольку имеют ненулевые коэффициенты только на главной диагонали, идущей от верхнего левого угла к нижнему правому.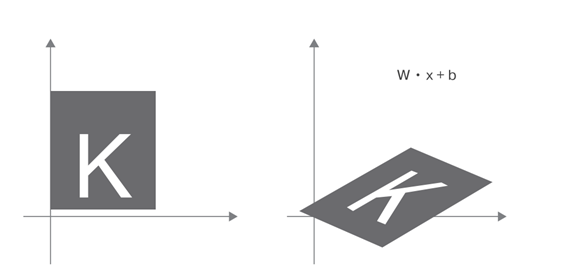

Линейное преобразование: скалярное произведение с произвольной матрицей реализует линейное преобразование. Обратите внимание, что масштабирование и поворот, перечисленные выше, по определению являются линейными преобразованиями;

Аффинное преобразование: аффинное преобразование (слайд) — это комбинация линейного преобразования (путем скалярного произведения с некоторой матрицей) и параллельного переноса (путем сложения векторов):

y = W • x + b

Благодаря им можно создать цепочку слоев для реализации очень сложных нелинейных геометрических преобразований и получить богатое пространство гипотез для глубоких нейронных сетей.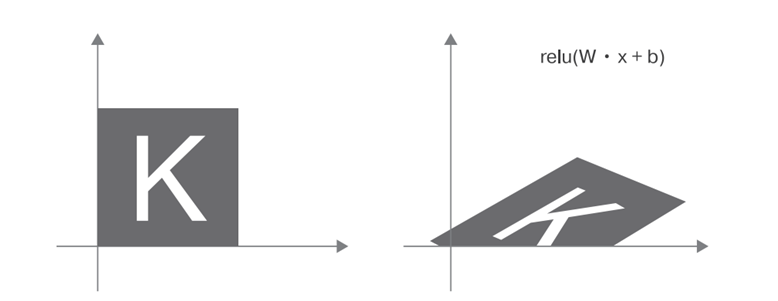

В качестве функции активации может использоваться операция relu: relu(x) — эквивалентна операции max(x, 0).

Название relu происходит от английского rectified linear unit (блок линейной корректировки).

45. Математические основы нейронных сетей. Цикл обучения.

46. Математические основы нейронных сетей. Оптимизация на основе градиента.

47. Математические основы нейронных сетей. Стохастический градиентный спуск.

48. Математические основы нейронных сетей. Алгоритм обратного распространения ошибки.

49. Глубокое обучение в технологиях компьютерного зрения. Сверточные нейронные сети.

Сверточные нейронные сети — разновидность моделей глубокого обучения, практически повсеместно используемые в приложениях компьютерного зрения (распознавания образов). Основным достоинством сверточных нейронных сетей при решении задач классификации изображений является использование небольшого объема обучающих данных.

Основное отличие полносвязного слоя от сверточного заключается в следующем: полносвязные слои изучают глобальные шаблоны в пространстве входных признаков (например, в случае с цифрами это шаблоны, вовлекающие все пиксели), тогда как сверточные слои изучают локальные шаблоны: в случае с изображениями — шаблоны в небольших двумерных окнах во входных данных. Эта ключевая характеристика наделяет сверточные нейронные сети двумя важными свойствами:

1) шаблоны, которые они изучают, являются инвариантными в отношении переноса. После изучения определенного шаблона в правом нижнем углу картинки сверточная нейронная сеть сможет распознавать его повсюду, например в левом верхнем углу. Полносвязной сети пришлось бы изучить шаблон заново, появись он в другом месте. Это увеличивает эффективность сверточных сетей в задачах обработки изображений: таким сетям требуется меньше обучающих образцов для получения представлений, обладающих силой обобщения;

2) они могут изучать пространственные иерархии шаблонов. Первый сверточный слой будет изучать небольшие локальные шаблоны, такие как края, второй — более крупные шаблоны, состоящие из признаков, возвращаемых первым слоем, и т. д. Это позволяет сверточным нейронным сетям эффективно изучать все более сложные и абстрактные визуальные представления.

Свертка применяется к трехмерным тензорам, называемым картами признаков, с двумя пространственными осями (высотой и шириной), а также с осью глубины (или осью каналов). Для изображений в формате RGB размерность оси глубины равна 3, потому что имеется три канала цвета: красный (red), зеленый (green) и синий (blue).

Для черно-белых изображений, как в наборе MNIST, ось глубины имеет размерность 1 (оттенки серого).

Операция свертывания извлекает шаблоны из своей входной карты признаков и применяет одинаковые преобразования ко всем шаблонам, производя выходную карту признаков. Выходная карта признаков также является трехмерным тензором: у нее есть ширина и высота. Ее глубина может иметь любую размерность, потому что выходная глубина является параметром слоя, и разные каналы на этой оси. Изображения можно разбить на локальные шаблоны, такие как края, текстуры и т. д.

Свертки определяются двумя ключевыми параметрами:

- размером шаблонов, извлекаемых из входных данных (обычно 3 × 3 или 5 × 5);

- глубиной выходной карты признаков — количеством фильтров, вычисляемых сверткой.

Свертка работает методом скользящего окна: она двигает окно размером 3 × 3 или 5 × 5 по трехмерной входной карте признаков, останавливается в каждой возможной позиции и извлекает трехмерный шаблон окружающих признаков (с формой (высота_окна, ширина_окна, глубина_входа)).

Каждый такой трехмерный шаблон затем преобразуется (путем умножения тензора на матрицу весов, получаемую в ходе обучения, которая называется ядром свертки) в одномерный вектор с формой (выходная глубина).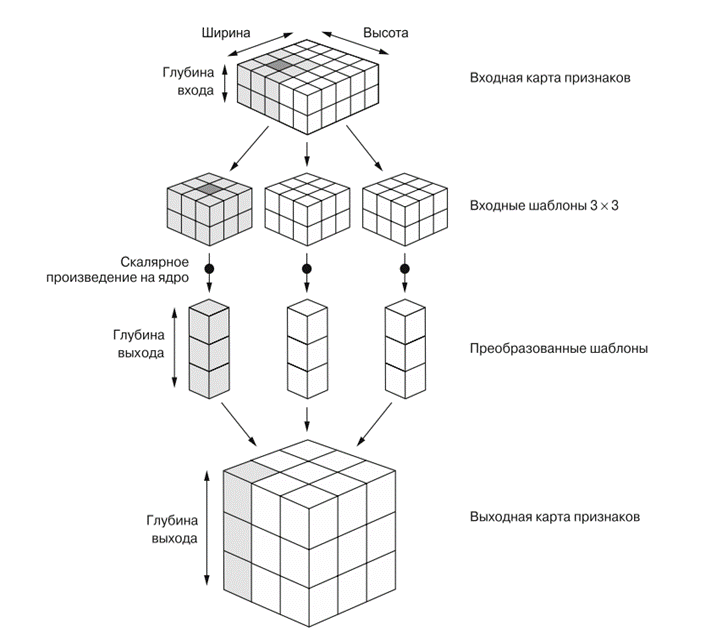

Все эти векторы затем собираются в трехмерную выходную карту с формой (высота, ширина, выходная глубина). Каждое пространственное местоположение в выходной карте признаков соответствует тому же местоположению во входной карте признаков (например, правый нижний угол выхода содержит информацию о правом нижнем угле входа).