История машинного обучения. Вероятностное моделирование. Метод опорных векторов. Деревья решений.
Вероятностное моделирование — применение принципов статистики к анализу данных. Это одна из самых ранних форм машинного обучения, которая до сих пор находит широкое использование. Одним из наиболее известных алгоритмов в данной категории является наивный байесовский алгоритм.
Наи́вный ба́йесовский классифика́тор — простой вероятностный классификатор, основанный на применении теоремы Байеса со строгими (наивными) предположениями о независимости входных данных.
В зависимости от точной природы вероятностной модели, наивные байесовские классификаторы могут обучаться очень эффективно. Несмотря на наивный вид и, несомненно, очень упрощенные условия, наивные байесовские классификаторы часто работают намного лучше нейронных сетей во многих сложных жизненных ситуациях.
Достоинством наивного байесовского классификатора является малое количество данных, необходимых для обучения, оценки параметров и классификации.
С байесовским алгоритмом тесно связана модель логистической регрессии. Модель логистической регрессии — это алгоритм классификации. Так же как наивный байесовский алгоритм, модель логистической регрессии была разработана задолго до появления компьютеров, но до сих пор остается востребованной благодаря своей простоте и универсальной природе. Часто это первое, что пытается сделать исследователь со своим набором данных, чтобы получить представление о классификации.
Ядерные методы — применение принципов статистики к анализу. Ядерные методы — это группа алгоритмов классификации, из которых наибольшую известность получил метод опорных векторов (Support Vector Machine, SVM).
Метод опорных
векторов — это алгоритм классификации,
предназначенный для поиска хороших
«решающих границ», разделяющих два
класса (см.слайд). Он выполняется в два
этапа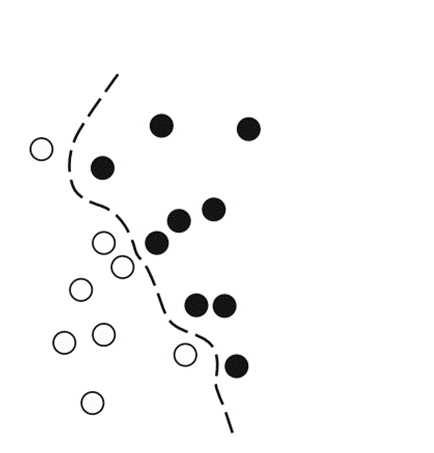
.
Данные отображаются в новое пространство более высокой размерности, где граница может быть представлена как гиперплоскость
Хорошая решающая граница (разделяющая гиперплоскость) вычисляется путем максимизации расстояния от гиперплоскости до ближайших точек каждого класса. Этот этап называют максимизацией зазора. Он позволяет обобщить классификацию новых образцов, не принадлежащих обучающему набору данных.
Деревья
решений —
это иерархические структуры, которые
позволяют классифицировать входные
данные или предсказывать выходные
значения по заданным исходным значениям.
Они легко визуализируются и интерпретируются.
Деревья решений, формируемые на основе
данных, заинтересовали исследователей
в 2000-х, и к 2010 году им часто отдавали
предпочтение перед ядерными методами.
В 2011 году, как раз перед тем, как глубокое обучение вышло на лидирующие позиции, общие инвестиции венчурного капитала в ИИ по всему миру составили меньше одного миллиарда долларов — эти деньги почти полностью ушли на практическое применение методов поверхностного машинного обучения.
К 2015 году вложения превысили пять миллиардов, а в 2017 достигли ошеломляющих 16 миллиардов (слайд). Кроме этого, крупные компании, такие как Google, Amazon и Microsoft, инвестировали деньги в исследования, проводившиеся внутренними подразделениями, и объемы этих инвестиций почти наверняка превысили вложения венчурного капитала.
Одним из ключевых факторов, обусловивших приток новых лиц в глубокое обучение, стала демократизация инструментов, используемых в данной области. На начальном этапе глубокое обучение требовало значительных знаний и опыта программирования на C++ и владения CUDA, чем могли похвастаться очень немногие.
В настоящее время для исследований в области глубокого обучения достаточно базовых навыков программирования на Python. Это вызвано прежде всего развитием Theano и позднее TensorFlow (двух фреймворков для Python, реализующих операции с тензорами, которые поддерживают автоматическое дифференцирование и значительно упрощают реализацию новых моделей), а также появлением дружественных библиотек (например, Keras).