Глубокое обучение. Принцип действия глубокого обучения. Геометрическая интерпретация глубокого обучения.
Глубокое обучение — особый раздел машинного обучения, новый подход к поиску представления данных, делающий упор на изучении последовательных слоев (или уровней) все более значимых представлений.
Под «глубиной» в глубоком обучении не подразумевается более детальное понимание, достигаемое этим подходом; идея заключается в создании многослойного представления. Поэтому подходящими названиями для этой области машинного обучения могли бы также служить многослойное обучение или иерархическое обучение.
Число слоев, на которые делится модель данных, называют глубиной модели. Современное глубокое обучение часто вовлекает в процесс десятки и даже сотни последовательных слоев представления — все они автоматически определяются на основе обучающих данных.
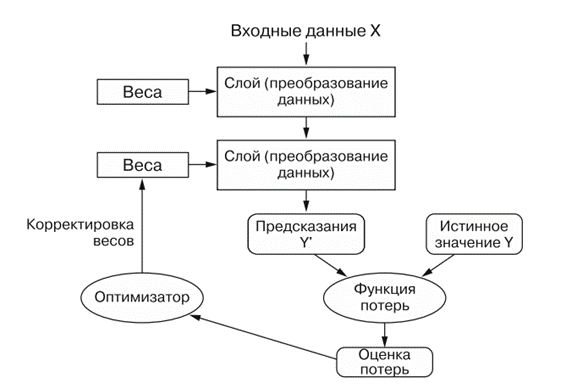
То, что именно слой делает со своими входными данными, определяется его весами, которые фактически являются набором чисел. Выражаясь техническим языком, преобразование, реализуемое слоем, параметризуется весами. (Веса также иногда называют параметрами слоя.)
В данном контексте обучение — это поиск набора значений весов всех слоев в сети, при котором сеть будет правильно отображать образцы входных данных в соответствующие им результаты.
Чтобы чем-то управлять, сначала нужно получить возможность наблюдать за этим. Чтобы управлять результатом работы нейронной сети, нужно измерить, насколько он далек от ожидаемого. Эту задачу решает функция потерь сети, называемая также целевой функцией или функцией стоимости. Функция потерь принимает предсказание, выданное сетью, и истинное значение (которое сеть должна была вернуть) и вычисляет оценку расстояния между ними, отражающую, насколько хорошо сеть справилась с данным конкретным примером.
Основная хитрость глубокого обучения заключается в использовании этой оценки для корректировки значения весов с целью уменьшения потерь в текущем примере (слайд). Данная корректировка является задачей оптимизатора, который реализует так называемый алгоритм обратного распространения ошибки — центральный алгоритм глубокого обучения.
Первоначально весам сети присваиваются случайные значения, то есть фактически сеть реализует последовательность случайных преобразований. Естественно, получаемый ею результат далек от идеала, и оценка потерь при этом очень высока. Но с каждым примером, обрабатываемым сетью, веса корректируются в нужном направлении и оценка потерь уменьшается.
Это цикл обучения, который повторяется достаточное количество раз (обычно десятки итераций с тысячами примеров) и порождает весовые значения, минимизирующие функцию потерь. Сеть с минимальными потерями, возвращающая результаты, близкие к истинным, называется обученной сетью.
Нейронную сеть можно интерпретировать как сложное геометрическое преобразование в многомерном пространстве, реализованное в виде последовательности простых шагов.
Иногда в трехмерном пространстве полезно представить следующий мысленный образ. Пусть мы имеем два листа цветной бумаги: один красного цвета и другой — синего. Положим их друг на друга и сомнем в маленький комок. Этот мятый бумажный комок — имитирует входные данные, а каждый лист бумаги — класс данных в задаче классификации.
Суть работы нейронной сети (или любой другой модели машинного обучения) заключается в таком преобразовании комка бумаги, чтобы разгладить его и сделать два класса снова ясно различимыми. В глубоком обучении это реализуется как последовательность простых преобразований в трехмерном пространстве, как если бы вы производили манипуляции пальцами с бумажным комком по одному движению за раз.
Разглаживание комка бумаги — вот в чем суть машинного обучения: в поиске ясных представлений для сложных, перемешанных данных. Это объясняет, почему глубокое обучение преуспевает в этом: оно использует последовательное разложение сложных геометрических преобразований в длинную цепь простых — почти так же, как поступает человек, разворачивая смятый лист. Каждый слой в глубоком обучении применяет преобразование, которое немного распутывает данные, а использование множества слоев позволяет работать с очень сложными данными.