Способы описания сетей Петри.
Существует несколько подходов к описанию СП:
- матричное описание;
- алгебраическое описание;
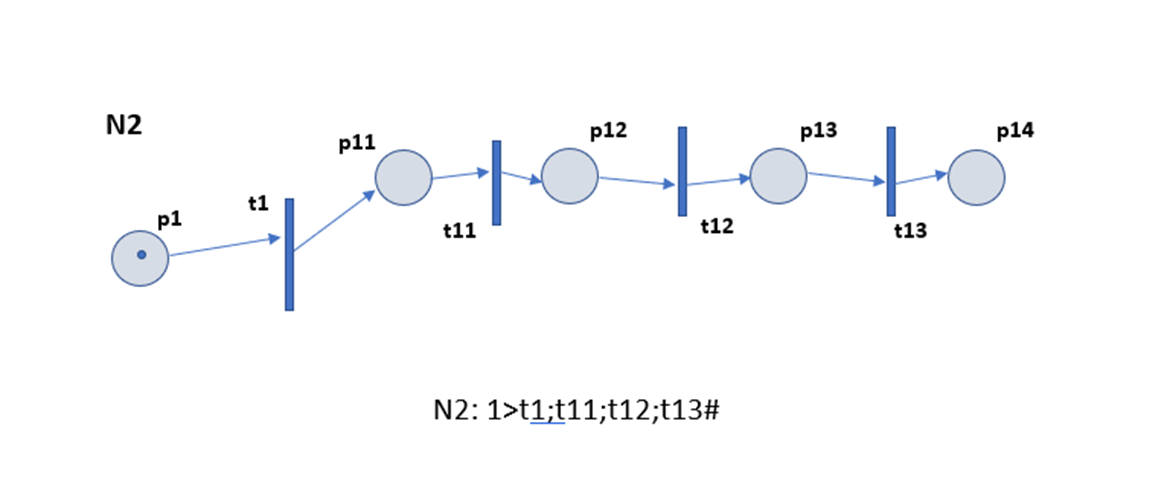
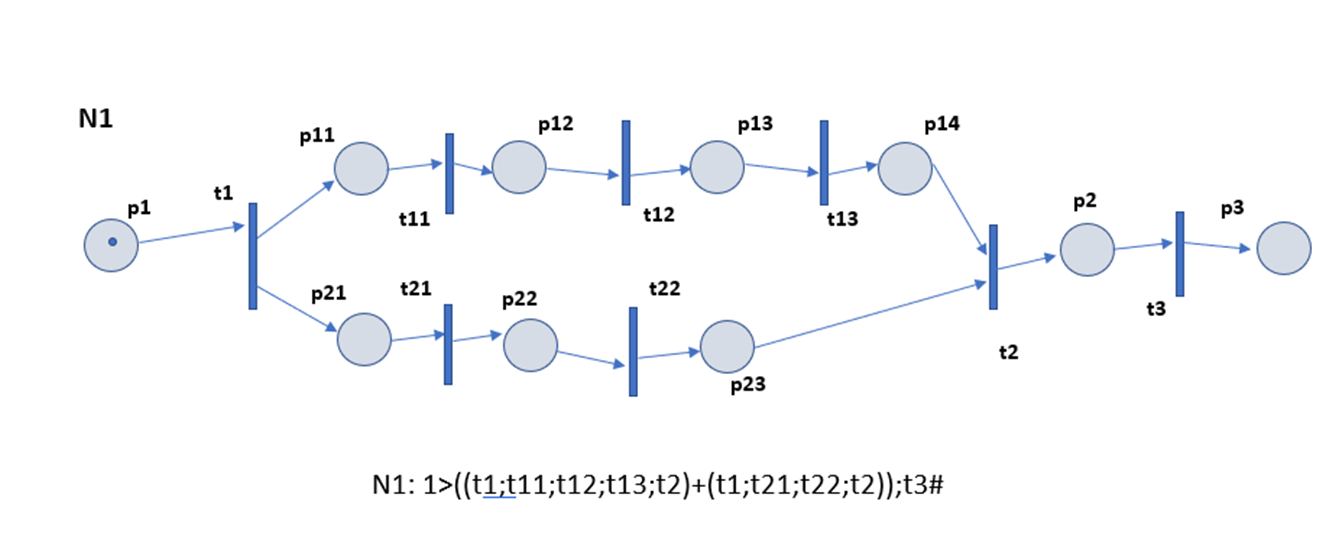
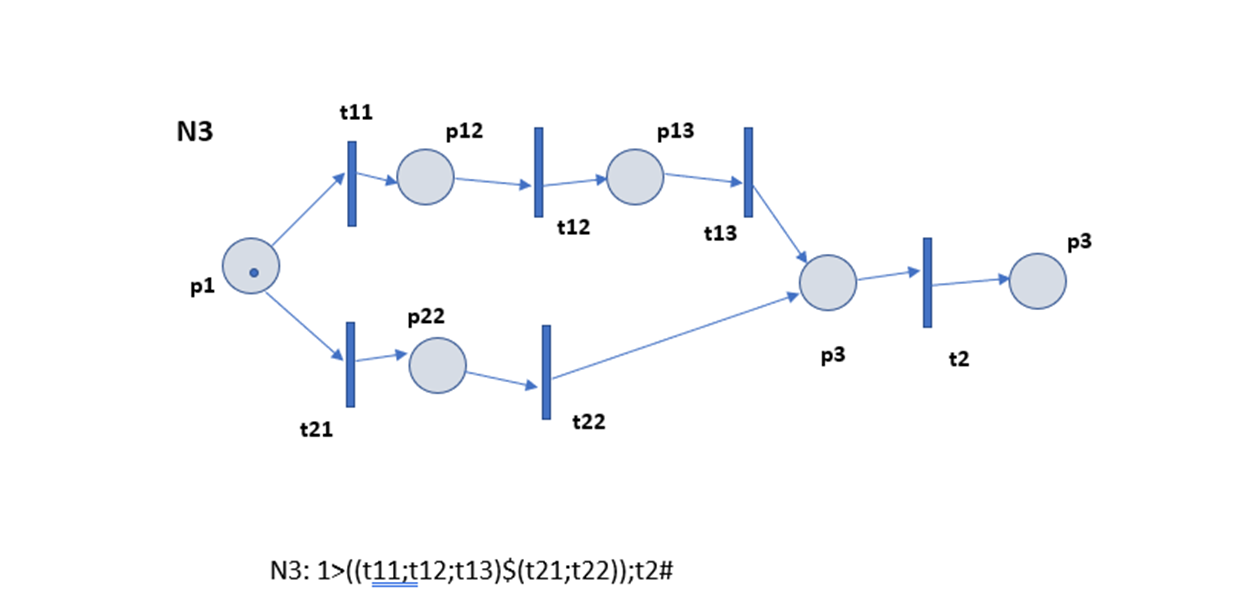
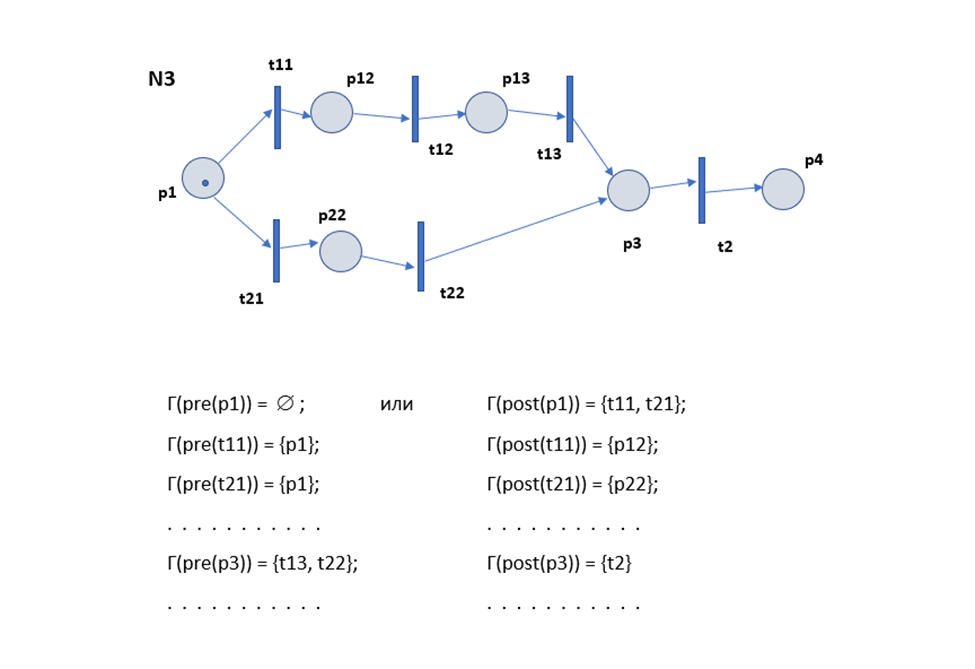
- описание на основе базовых фрагментов;
- графическое описание.
Методы анализа сетей Петри. Задачи анализа.
Одним из важнейших свойств СП, моделирующей реальное устройство, является безопасность. Известно, что если позиция безопасна, то число меток в ней равно 0 или 1.
Безопасность - это частный случай более общего свойства ограниченности.
Другим важным свойством СП является наличие или отсутствие тупиковых ситуаций. Тупики в реальных системах возникают при распределении ресурсов между взаимодействующими процессами и служат предметом многих исследований в области сложных систем. В СП-модели аналогом тупиковых ситуаций являются тупиковые разметки.
Задача достижимости формулируется следующим образом:
для СП N с начальной разметкой m0 и разметкой m' определить m0 ® m’ , то есть существует ли последовательность переходов ν , срабатывание которых переводит разметку m0 в m’ .
Задача достижимости является основной задачей анализа СП. Многие другие задачи анализа можно сформулировать в терминах задачи достижимости.
В настоящее время наиболее широко используются два метода анализа СП, которые позволяют решить некоторые из перечисленных задач:
1 - построение дерева достижимых разметок,
2 – метод, основанный на решении матричных уравнений.
Методы анализа сетей Петри. Дерево достижимых разметок.
Методы анализа сетей Петри. Анализ на основе матричных методов.
Показано, что если СП живая и ограниченная, то она должна быть последовательной и инвариантной. Данные свойства недостаточны для утверждения живости и ограниченности СП. Однако их полезно проверить исходя из матриц инцидентности, так как если одно из этих свойств не подтверждается, то можно заключить, что описываемая система содержит некоторые недоработки.
Инвариантные и последовательные сети Петри . Введем в рассмотрение матрицу С, которая получается следующим образом:
C = O - I .
Пусть размерность С равна n ´ m , где m и n мощности множеств P и T .
Рассмотрим матричные уравнения :
C * x = 0 ; (1)
y * C = 0 , (2)
где x и y - векторы, размерность которых равна n и m соответственно.
Вектор у, удовлетворяющий решению уравнения (1) и все элементы которого положительны, называется р-цепью; р-цепь, все элементы которой больше нуля, называется полной р-цепью.
Анaлогично на основе уравнения (2) определяются понятия t-цепи и полной t-цепи.
СП, для которой существует полная р-цепь, называется инвариантной. СП, для которой существует полная t-цепь, называется последовательной .
Проектирование сложных вычислительных структур. Структурный подход.
Использование сетевых моделей, основанных на сетях Петри (СП), всегда привлекало исследователей, начиная с момента появления данного формализма. В настоящее время, с возрастанием интереса к распределенным структурам, многоагентным системам и алгоритмам взаимодействия отдельных подсистем, интерес к СП только возрастает.
Аппарат СП широко используется при решении вопросов, связанных с проектированием и верификацией сложных систем, с построением программных средств на основе сетевых моделей и оценки возможности распараллеливания программ, с применением сетевых моделей для описания и анализа автоматизированных систем, сетевых протоколов, вычислительных сетей, многопроцессорных системы и др.
Кроме этого, СП являются инструментом, эффективно поддерживающим структурный подход к проектированию сложных систем. При использовании структурного подхода выделяют следующие основные этапы:
1) описание функций, которые должна выполнять проектируемая система;
2) выработка ряда гипотез, касающихся структур подсистем, из которых будет состоять проектируемая система (декомпозиция);
3) формирование из данных подсистем законченных структур-кандидатов (синтез);
4) проведение анализа каждой синтезированной структуры с целью определения характеристик, что позволяет сократить число структур-кандидатов и, в конечном итоге, выбрать окончательную структуру, наилучшим образом описывающую систему с заданным функционалом.
Инвариантом при прохождении данных этапов является функционал, заложенный при описании проектируемой системы.
При исследовании свойств СП-моделей было показано, что множество синтезированных СП-моделей (структур-кандидатов), образует метрическое пространство, на котором можно ввести различные шкалы, количественно оценивающие каждую СП-модель.
Наличие механизма построения альтернативных структур-кандидатов, а также наличие инструментария количественной оценки данных структур, позволяет проектировщику получить все множество возможных структур, реализующих заданный функционал, и выбрать из этого множества структуры, являющиеся оптимальными по заданному критерию.
Проблема использования описанного подхода на практике состоит в NP-сложности задачи получения множества альтернативных вариантов, что существенно ограничивает практическое использование данного подхода.
Одним из подходов при решении проблем NP-сложности является ввод ряда ограничивающих условий (построение базы знаний), позволяющих уменьшить число рассматриваемых вариантов, и тем самым снизить сложность решаемой задачи.
Одним из методов достижения высокой производительности систем обработки данных реального времени является использование процессорных матриц – специализированных вычислительных структур, состоящих из множества относительно простых устройств (процессорных элементов), объединённых в однородные параллельные системы.
Рассмотрим подход к проектированию различных конфигураций матричных процессоров, основанный на структурном анализе сетей Петри и тензорной методологии.