Физика (Контрольная работа №1)
.docx
Федеральное
агентство железнодорожного транспорта
Приморский институт железнодорожного транспорта - филиал
Федерального государственного бюджетного образовательного
учреждения высшего образования
«Дальневосточный государственный университет путей сообщения»
в г. Уссурийске
Факультет высшего образования
КОНТРОЛЬНАЯ РАБОТА № 1
«Расчёт радиуса-вектора центра масс механической системы»
(вариант 1)
Выполнил: студент 1курса
Балаченков А.Н.
группа сзп14опу
Руководитель:
доцент Ким В.С.
Уссурийск
2021
Введение
Данная контрольная работа преследует цель практического обучения вычисления положения центра масс механической системы образованной 20 точками, имеющими различную массу. Вычисления производим путём построения точек в системе координат согласно данных для своего варианта и их соединения в контур тела , после чего приблизительно (на глаз) определяем центр массы тела и проставляем его , далее производим расчёт реального положения радиуса-вектора центра масс и так же фиксируем результат проставляя точку в системе координат, сравниваем получившиеся результаты. На основе сравнения делаем выводы о возможности определять приблизительно центр массы тела без сопутствующих расчётов.
Часть первая
Закон всемирного тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 × 10-11м3·кг-1·с-2 |
Данная формула приведена в [1]
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Сила тяжести — сила, действующая на любое физическое тело вблизи поверхности астрономического объекта (планеты, звезды) и складывающаяся из силы гравитационного притяжения этого объекта и центробежной силы инерции, вызванной его суточным вращением.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с2]
На земле g = 9,8 м/с2
Данная формула приведена в [3]
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении. Ускорение свободного падения для каждой планеты уникально.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически. Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается.
Часть вторая
Согласно задания начертим систему координат X0Y содержащую механическую систему (тело) имеющего в заданных точках определённую массу.
Точки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
m= |
2 |
3 |
4 |
5 |
4 |
3 |
2 |
1 |
2 |
3 |
4 |
5 |
4 |
3 |
2 |
1 |
2 |
3 |
4 |
5 |
X |
-6 |
-5 |
-3 |
-1 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
13 |
15 |
13 |
10 |
8 |
5 |
1 |
4 |
6 |
Y |
15 |
16 |
18 |
20 |
18 |
16 |
14 |
12 |
12 |
12 |
12 |
6 |
4 |
2 |
-1 |
1 |
4 |
8 |
9 |
6 |
Выберем на чертеже и отметим приблизительную точку центра масс , отметим её синим
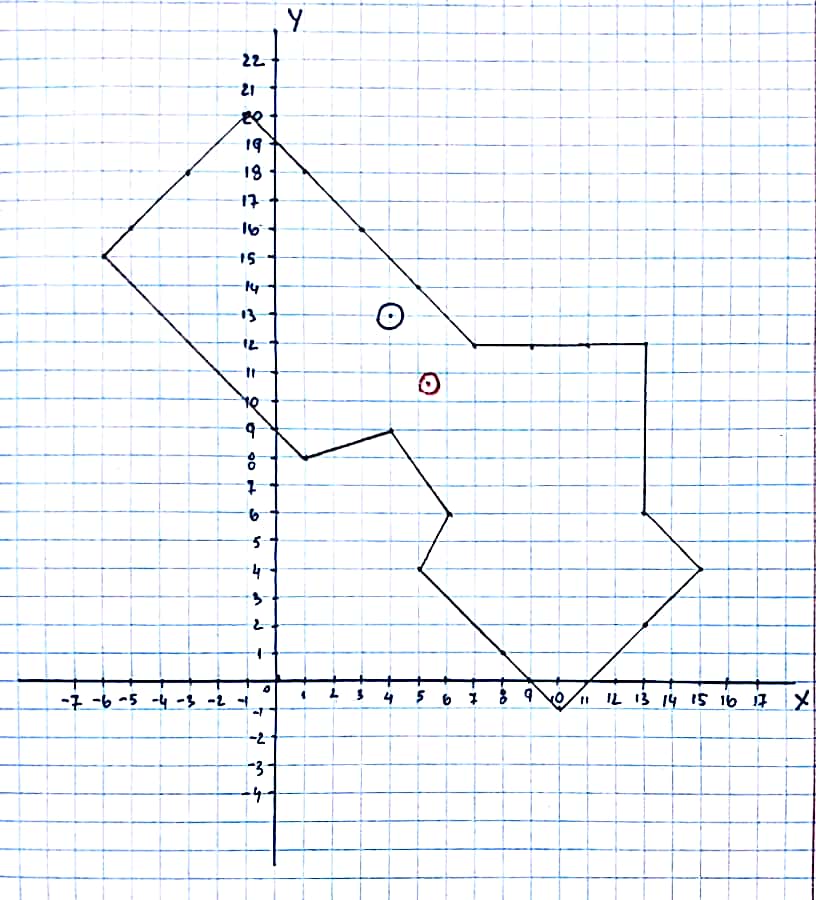
Выпишем координаты приблизительной точки.
Далее согласно формуле расчёта радиуса-вектора центра масс
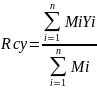
Где
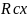– проекция
на ось 0X
– проекция
на ось 0Y
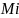– масса
i
точки
- X
координата i
точки
- Y
координата i
точки
Вычислим центр масс для своего варианта
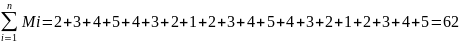
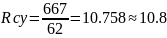
Нанесем получившуюся точку радиуса-вектора центр масс на систему координат красным цветом.
Заключение
Основываясь на полученных результатах несовпадения приблизительной точки радиуса-вектора центра масс и точки полученной в результате расчёта можно смело сделать вывод о том что приблизительное определение центра тяжести не приносит никаких полезных данных и не может быть использовано на практике в отличии от данных полученных путём вычислений, так как несовпадение может быть критичным и при определённых обстоятельствах стать одной из причин каких либо отрицательных событий.
Литература:
Закон всемирного тяготения https://elementy.ru/trefil/23/Zakon_vsemirnogo_tyagoteniya_Nyutona
Трофимова Т.И. «Курс физики-2006. 11 издание»
Закон всемирного тяготения «Карина Хачатурян. Рубрика 9 класс/ЕГЭ» https://skysmart.ru/articles/physics/zakon-vsemirnogo-tyagoteniya
Определение центра масс «сайт Webmath.ru» https://www.webmath.ru/poleznoe/fizika/fizika_114_opredelenie_centra_mass.php
Не найдены в общем доступе
Буркова И.Н. Измерение физических величин , обработка и предоставление результатов измерения Хабаровск 2012
Ким В.С. Физика. Конспект лекций. (Рукопись) – Уссурийск 2021