
lab_4_novella
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Информатика»
Лабораторная работа №4
«Моделирование простейших логических схем»
по дисциплине:
«Математическая логика и теория алгоритмов»
Выполнил: студент группы
Рулев Д.В Вариант №23(7)
Проверил: Семин Валерий Григорьевич
Москва 2023
Задание 1. Таблица истинности для задания определяется датой дня рождения студента. Для этого необходимо дату представить в формате ДД:ММ:Гг. Десятилетие Г исключается (просто откидывается). В результате получаем ДДММг. Полученное число нужно перевести в двоичный формат представления данных. Результат необходимо дополнить до 16 разрядов дописав перед числом необходимое количество нулей. Реализовать полученную функцию на логических элементах.
ДДММг =03010
Перевод 03010 из 10 системы счисления в 2:
3010:2=1505(0)
1505:2=752(1)
752:2=376(0)
376:2=188(0)
188:2=94(0)
94:2=47(0)
47:2=23(1)
23:2=11(1)
11:2=5(1)
5:2=4(1)
4:2=2(0)
2:2=1

Дополним
до 16-ти разрядов 0000
Составим таблицу истинности:
|
|
|
|
F |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
В логической функции количество единиц меньше, чем нулей. Поэтому используем СДНФ (совершенную дизъюнктивную нормальную форму).

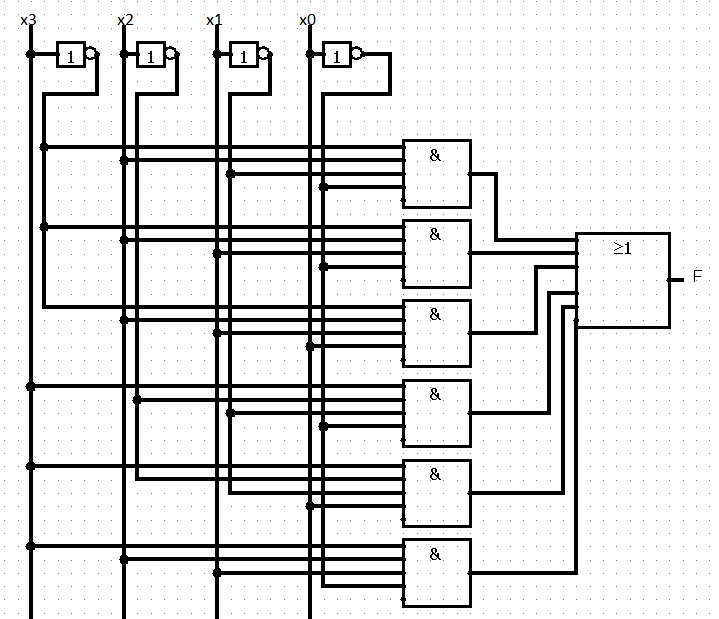
Рис.1 – Схема реализации функции на логических элементах
Задание 3. Выполнить минимизацию по карте Карно, синтезировать схему на базисе, определенного вариантом, привести синтезируемую схему, выполнить проверку на соответствие исходной таблице истинности. 1 - 4 вариант -> И-НЕ 5 - 8 вариант -> ИЛИ-НЕ 9 - 12 вариант -> И-НЕ 13 - 16 вариант -> ИЛИ-НЕ
1)Составим карту карно
x1x0
x3x4 |
00 |
01 |
11 |
10 |
00 |
0 |
0 |
0 |
0 |
01 |
1 |
0 |
1 |
1 |
11 |
0 |
0 |
0 |
1 |
10 |
1 |
1 |
0 |
0 |
x1x0
x1x4 |
00 |
01 |
11 |
10 |
00 |
0 |
0 |
0 |
0 |
01 |
1 |
0 |
1 |
|
11 |
0 |
0 |
0 |
1 |
10 |
1 |
1 |
0 |
0 |
1)
1 область, где …
объединяются
10 по
 и 0001 по
и 0001 по
 ,
остается неизменным(т.к. 1),
меняется
с отрицанием(т.к. 0)
,
остается неизменным(т.к. 1),
меняется
с отрицанием(т.к. 0) (т.к.
00),
исчезает( т.к. меняется с 0 на 1), получаем
f0=
(т.к.
00),
исчезает( т.к. меняется с 0 на 1), получаем
f0=
2)
2 область, где …
объединяются 01 по
и 00 по
,
меняется
со знаком отрицания (т.к. 0),
остается неизменным(т.к. 1),
 меняются со знаком отрицания(т.к. 00),
получаем f1=
меняются со знаком отрицания(т.к. 00),
получаем f1=

3)
3 область, где объединяются 0111 по
и 10 по
,
 остается неизменным (т.к. 11),
остается неизменным (т.к. 1),
остается неизменным (т.к. 11),
остается неизменным (т.к. 1), , получаем f2=
, получаем f2=
4)
4 область, где …
объединяются 01 по
и 1110 по
,
,
меняется с отрицанием (т.к. 0),
остается
неизменным (т.к. 1),
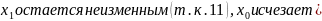
Меняется
на 0) получаем f3=
F=f0+f1+f2+f3
F=
Переход в базис ИЛИ-НЕ:
F=

Рис.2 – Схема реализации функции в базисе ИЛИ-НЕ
Таблица истинности для функции в базисе ИЛИ-НЕ
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
F |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |





 1
1


