
КР Сопротивление материалов
.docxФедеральное агентство железнодорожного транспорта
Приморский институт железнодорожного транспорта - филиал
Федерального государственного бюджетного образовательного
учреждения высшего образования
«Дальневосточный государственный университет путей сообщения»
в г. Уссурийске
Факультет высшего образования
КОНТРОЛЬНАЯ РАБОТА
По предмету «Прикладная механика: Сопротивление материалов»
Выполнил: студент 1курса
А.Н.
группа сзп14опу
шифр КТ21-ЭЖД(СТ)-556
проверил: Тряпкин Д.А.
Уссурийск
2022
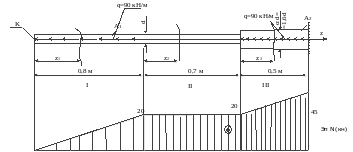
ЗАДАЧА 3.
1. Вычертить расчетную схему в определенном масштабе, указать все размеры и величины нагрузок в числах.
2. Построить эпюры внутренних усилий.
Решение
Построение эпюр продольных сил. Используя метод сечения определим значения продольной силы в каждом из участков.
Участок
I,
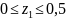 м
м
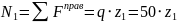
На этом участке получили уравнение прямой. Для построения прямой достаточно знать две точки. Найдем значения продольной силы на концах участка:
при
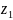 =0
м
=0
м
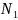 =0
кН; при
=0,5 м
=5
кН (сила растягивающая)
=0
кН; при
=0,5 м
=5
кН (сила растягивающая)
Участок
II,
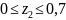 м
м
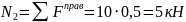 На
этом участке сила постоянна
На
этом участке сила постоянна
Участок
III,
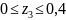 м
м
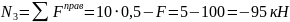
На этом участке сила постоянна
По
найденным значениям продольной силы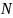 строим эпюру.
строим эпюру.
ЗАДАЧА 4.
1. Вычертить расчетную схему в определенном масштабе, указать все размеры и величины нагрузок в числах.
2. Построить эпюры внутренних усилий.
Решение
Построение эпюр крутящих моментов.
1. Определим
значение неизвестного момента, для
этого запишем уравнение равновесия
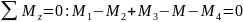 .
Откуда
.
Откуда
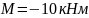
2.Используя метод сечения определим значения крутящего момента в каждом из участков.
Участок
I,
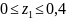 м
м
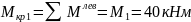
Участок II, м
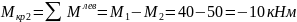
Участок
III,
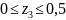 м
м
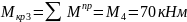
Участок
IV,
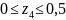 м
м
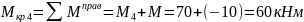
По
найденным значениям
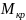 строим эпюру.
строим эпюру.

ЗАДАЧА 5.
1. Вычертить расчетную схему в определенном масштабе, указать все размеры и величины нагрузок в числах.
2. Построить эпюры внутренних усилий.
Решение
Строим
эпюры поперечных сил
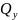 и изгибающих моментов
и изгибающих моментов
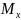 .
.
1.
Определение реакции опор
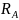 ,
,
 и их проверка.
и их проверка.
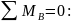
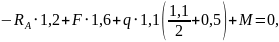
откуда
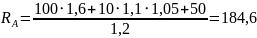 кН.
кН.
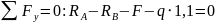 ,
,
откуда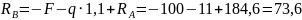 кН.
кН.
Проверка
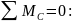
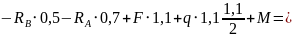
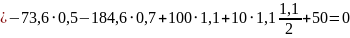
Используя метод сечения определим значения внутренних усилий в каждом из участков.
Участок I: м

На
этом участке поперечная сила имеет вид
прямой. Найдем значения
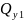 на концах участка: при
на концах участка: при
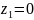
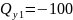 кН,
при
кН,
при
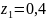 м
м
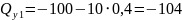 кН.
кН.
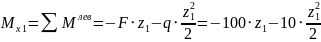
На
этом участке изгибающий момент вид
параболы. Найдем значения изгибающего
момента на концах участка и по середине.
При
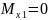 ,
при
м
,
при
м
 кНм., при
кНм., при
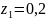 м
м
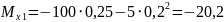 кНм.
кНм.
Участок
II
 м
м
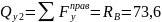 кН
кН
На этом участке поперечная сила постоянна
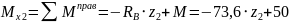 (прямая)
(прямая)
при
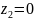
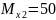 кНм,
при
кНм,
при
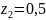 м
м
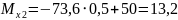 кНм.
кНм.
Участок
III
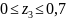 м
м
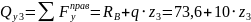 (прямая)
(прямая)
при
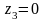
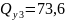 кН,
при
кН,
при
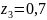 м
м
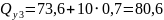 кН.
кН.
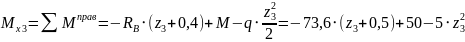 (парабола)
(парабола)
при
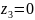
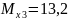 кНм,
кНм,
при
м
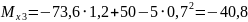 кНм.
кНм.
при
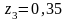
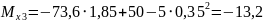 кНм.
кНм.
По
найденным значениям
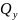 и
и
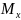 строим эпюры
строим эпюры
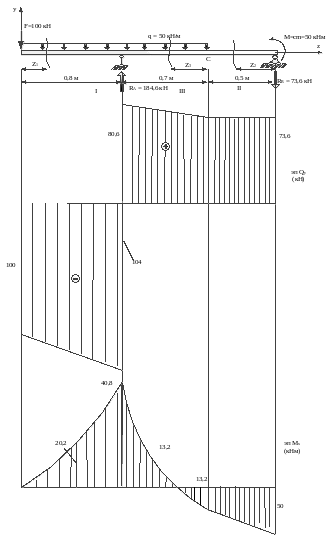
ЗАДАЧА 6.
1. Вычертить расчетную схему в определенном масштабе, указать все размеры и величины нагрузок в числах.
2. Построить эпюры внутренних усилий.
Решение
1.
Определение реакции опор
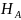 ,
,
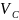 ,
,
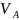 и их проверка.
и их проверка.
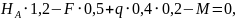
откуда
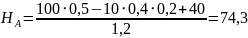 кН.
кН.
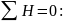
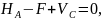
откуда
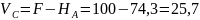 кН.
кН.
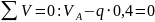 ,
,
откуда
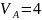 кН.
кН.
Проверка:
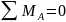
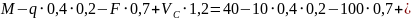
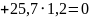 .
.
2. Построение эпюр , и .
Участок
I
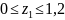 м
м
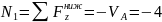 кН,
кН,
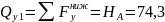 (постоянная),
(постоянная),
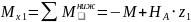 (прямая),
(прямая),
при
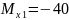 кНм,
при
кНм,
при
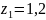 м
м
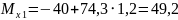 кНм.
кНм.
Участок
II
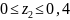 м
м
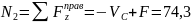 кН
кН
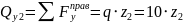 кН
(прямая)
кН
(прямая)
при
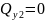 кН,
при
кН,
при
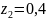 м
м
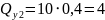 кН,
кН,
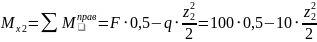 (парабола),
(парабола),
при
кНм,
при
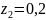 м
м
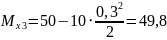 кНм,
кНм,
при
м
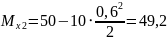 кНм.
кНм.
Участок III м
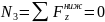 кН,
кН,
 (постоянная),
(постоянная),
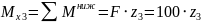 (прямая),
(прямая),
при
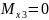 ,
при
,
при
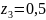 м
м
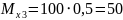 кНм.
кНм.
По найденным значениям , и строим эпюры.
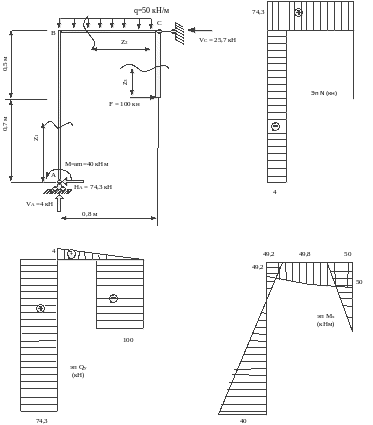
Проверим правильность построения эпюр , и , для этого выполним статическую проверку. Вырежим узлы В, С и проверим их равновесие .
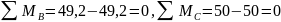
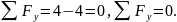
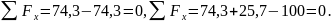
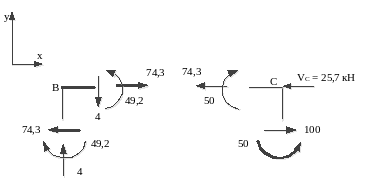
ЗАДАЧА 7.
Найти
размеры поперечного сечения стержня
(d=?) при [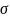 ]=20МПа.
Построить эпюру распределения напряжений
в опасном сечении. Определить перемещение
]=20МПа.
Построить эпюру распределения напряжений
в опасном сечении. Определить перемещение
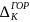 при
модуле упругости Е=3∙
при
модуле упругости Е=3∙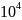 МПа.
МПа.
Решение:
1.Построение эпюры продольных сил :
Участок
I
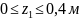

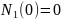 ;
;
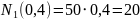 кН;
кН;
Участок
II
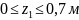
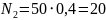 кН.
кН.
Участок
III

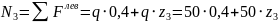 ;
;
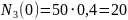 кН;
кН;
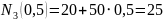 кН.
кН.
2. Определение нормальных напряжений в сечениях:
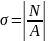 ,
где:
-нормальное
напряжение;
- продольная
сила в сечении; А -
,
где:
-нормальное
напряжение;
- продольная
сила в сечении; А -
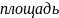 поперечного сечения.
поперечного сечения.
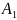 =
=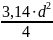 =0,785∙
=0,785∙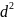 ;
;
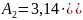 =2,01∙
.
=2,01∙
.
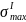 =
=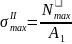 =
=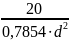 =
=
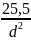 ;
;
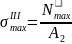 =
=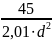 =
=
 ;
;
Условие
прочности при растяжении (сжатии):
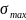 =
=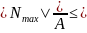 [
],
где:
- наибольшее нормальное напряжение;
[
],
где:
- наибольшее нормальное напряжение;
 - наибольшее значение продольной
силы;
- наибольшее значение продольной
силы; [
]=20
МПа=2 кН/
[
]=20
МПа=2 кН/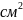 -допускаемое
нормальное напряжение.
-допускаемое
нормальное напряжение.
=
 ;
d
;
d
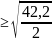 ;
d
;
d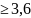 cм.
cм.
Принимаем размеры поперечного сечения: d=3,6 см, αd=1,6∙3,6=5,7 см.
2. Эпюра распределения нормальных напряжений в опасном сечении
=
=
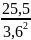 =
1,9 кН/
=
1,9 кН/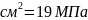

Определение горизонтального перемещения точки К при модуле упругости Е=3∙ МПа=3∙
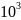 кН/
:
перемещение
будем искать по формуле
кН/
:
перемещение
будем искать по формуле
 ,
,
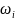 - площадь
эпюры N
на каждом участке.
- площадь
эпюры N
на каждом участке.
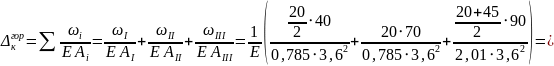
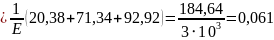 см.
см.
ЗАДАЧА 8.
Проверить
прочность вала круглого поперечного
сечения диаметром 10 см при
 =80 МПа. В случае невыполнения условия
прочности подобрать диаметр вала.
Построить эпюру распределения напряжений
в опасном сечении. Определить перемещение
=80 МПа. В случае невыполнения условия
прочности подобрать диаметр вала.
Построить эпюру распределения напряжений
в опасном сечении. Определить перемещение
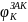 при
модуле сдвига G=8∙
МПа.
при
модуле сдвига G=8∙
МПа.
Решение:
1.
Построение эпюры крутящих моментов
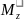
участок
I:
 =
=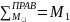 =
16 кНм;
=
16 кНм;
участок
II:
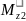 =
=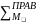 =
16 кНм;
=
16 кНм;
участок
III:
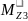 =
=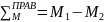 =16-20=-4
кНм.
=16-20=-4
кНм.
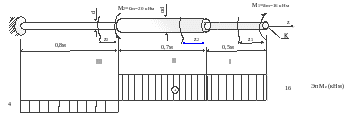
2. Проверка прочности вала на каждом участке:
Условие
прочности при кручении:
 ,
где :
,
где :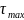 -наибольшее
касательное напряжение;
-наибольшее
касательное напряжение;
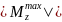 -значение
наибольшего крутящего момента по
абсолютной величине;
-значение
наибольшего крутящего момента по
абсолютной величине;
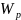 -полярный
момент сопротивления сечения;
=80
МПа=8кН/
-допускаемое
касательное напряжение.
-полярный
момент сопротивления сечения;
=80
МПа=8кН/
-допускаемое
касательное напряжение.
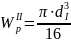 =
=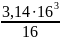 =803,84
=803,84
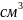 ;
;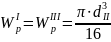 =
=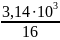 =196,25
=196,25
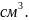
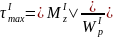 =
=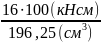 =8,1
кН/
>
=8,1
кН/
>
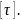
На
I
участке условие прочности вала не
выполняется. Необходимо подобрать
другой диаметр вала. Из условия прочности
(по максимальным напряжениям
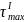 )
находим требуемый момент сопротивления
)
находим требуемый момент сопротивления
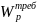 :
:
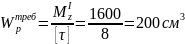 .
.
Тогда диаметр вала на участке I:
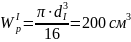 ,
откуда
,
откуда
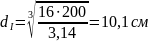 .
.
3. Эпюра распределения напряжений в опасном сечении
Опасным являются все сечения участка I.
Опасным являются все сечения участка I.
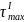 =
=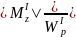 =
=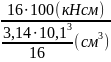 =8
кН/
=8
кН/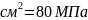
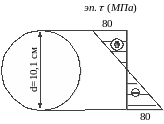
Перемещение
Перемещение
определим по формуле:
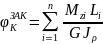 ,
где
,
где
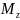 – крутящий
момент;
– крутящий
момент;
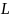 – длина скручиваемого участка;
– длина скручиваемого участка;
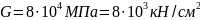 – модуль сдвига;
– модуль сдвига;
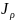 – полярный момент инерции сечения
вала.
– полярный момент инерции сечения
вала.
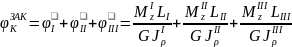 ,
,
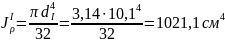 ,
,
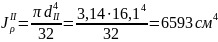 ,
,
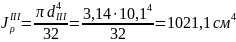 .
.
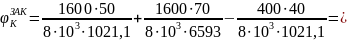
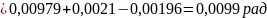 ;
;
ЗАДАЧА 9.
Определить
номер двутавровой балки при [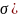 =160МПа,
[
=160МПа,
[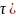 =110МПа.
Построить эпюры распределения напряжений
=110МПа.
Построить эпюры распределения напряжений
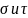 в опасных сечениях. Сделать проверку
прочности по главным напряжениям,
условно приняв М=
в опасных сечениях. Сделать проверку
прочности по главным напряжениям,
условно приняв М=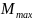 , Q=
, Q=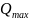 .
Определить перемещения
.
Определить перемещения
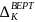 ,
,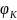 при модуле упругости Е=2∙
при модуле упругости Е=2∙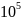 МПа.
МПа.
Решение:
1. Построение эпюр изгибающих моментов и поперечных сил
участок
I;
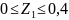
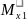 =∑
=∑ =
-50∙
=
-50∙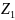 ∙
/2;
(0)=0;
(0,2)=
-50∙0,2∙0,2/2= -1кНм;
∙
/2;
(0)=0;
(0,2)=
-50∙0,2∙0,2/2= -1кНм;
(0,4)=
-50∙0,4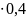 /2=
-4 кНм.
/2=
-4 кНм.
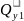 =∑
=∑ =
-50∙
;
(0)=0;
(0,4)=
-50∙0,4= -20кН.
=
-50∙
;
(0)=0;
(0,4)=
-50∙0,4= -20кН.
Участок
II:
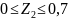
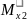 =∑
=-50∙0,4∙(0,2+
=∑
=-50∙0,4∙(0,2+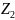 )+100∙
;
)+100∙
;
(0)=-4 кНм; (0,7)=-50∙0,4∙(0,2+0,7)+100∙0,7=52кНм;
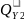 =∑
=
-50∙0,4+100=80.
=∑
=
-50∙0,4+100=80.
Участок
III:
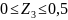
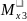 =∑
=-50∙0,4∙(0,2+0,7+
=∑
=-50∙0,4∙(0,2+0,7+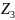 )+100∙(
)+100∙(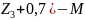 ;
;
(0)=-50∙0,4∙0,9+100∙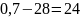 кНм;
кНм;
(0,5)
=-50∙0,4∙1,4+100∙1,2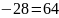 кНм.
кНм.
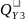 =∑
= 80кН.
=∑
= 80кН.

2. Определение номера двутавровой балки.
по нормальным напряжениям
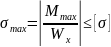 ,
,
вычисляем требуемый момент сопротивления
 .
.
Из
сортамента ГОСТ 8239-89 выбираем двутавр
№30 с
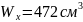 .
.
Проверяем принятый двутавр по нормальным и касательным напряжениям:
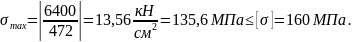
Из
сортамента для двутавра №33 выписываем
геометрические характеристики сечения:
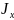 =7080
=7080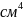 ;
;
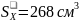 .
.
Наибольшее касательное напряжение вычислим по формуле Журавского
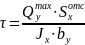 ,
,
где
Q – поперечная сила;
– момент инерции поперечного сечения
относительно оси х;
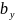 – ширина сечения балки в точке которой
определяем напряжение;
– ширина сечения балки в точке которой
определяем напряжение;
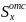 – статический момент отсеченной части
поперечного сечения относительно оси
х,
– статический момент отсеченной части
поперечного сечения относительно оси
х,
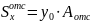 ,
где
,
где
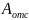 – площадь отсеченной части поперечного
сечения;
– площадь отсеченной части поперечного
сечения;
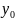 – расстояние от центра тяжести отсеченной
части поперечного сечения до оси х;
– расстояние от центра тяжести отсеченной
части поперечного сечения до оси х;
= =
=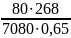 =3,94кН/
=3,94кН/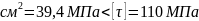 .
.
Таким образом, прочность балки по нормальным и касательным напряжениям выполняется.
3. Построение эпюр распределения напряжений
Точка 1:
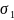 =
=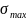 =135,6
Мпа;
=135,6
Мпа;
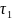 =0,
т.к.
=0,
т.к.
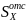 =0.
=0.
Точка 2:
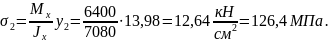
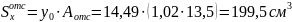 .
.
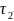 =
=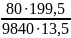 =0,14кН/
=0,14кН/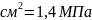 ,
,
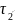 =
=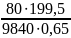 =2,8кН/
=2,8кН/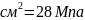 .
.
Точка 3:
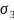 =0
Мпа;
=0
Мпа;
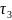 =
=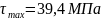 .
.
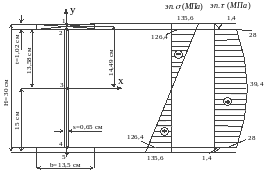
4.Проверка прочности по главным напряжениям.
=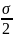 +
+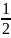 ∙
∙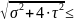 [
.
[
.
Наиболее опасной точкой является точка 2.
=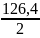 +
∙
+
∙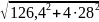 =132,3
МПа
=132,3
МПа [
[ .
.
Таким образом, прочность балки по главным напряжениям выполняется.
5.
Определение перемещений
,
при модуле упругости Е=2∙
Мпа=2∙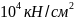 .
.
Прогиб балки в сечении “к”
=∑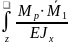 dz=
dz=
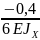 ∙(4∙0,4+4∙1∙0,2)+
∙(4∙0,4+4∙1∙0,2)+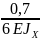 ∙(-2∙4∙0,4+2∙52∙1,1-
∙(-2∙4∙0,4+2∙52∙1,1-
-4∙1,1+52∙0,4)+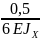 ∙(2∙24∙1,1+2∙1,6∙64+2∙24+1,1∙64)=
∙(2∙24∙1,1+2∙1,6∙64+2∙24+1,1∙64)=
=
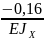 +
+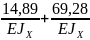 =
=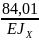 =
=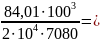 0,43 см
0,43 см
(перемещение со знаком (+), значит точка К перемещается по направлению силы F=1, то есть вверх).
