
Презентации лекций / Презентация лекции 15 ДМ 20
.pdf
Тема 15 «Паросочетанияв двудольных графах»
«Дискретная математика» Олейник Татьяна Анатольевна
кафедра ВМ-1

План лекции
1.Алгоритм поиска в ширину в ориентированном графе
2.Понятие паросочетания
3.Задачао наибольшем паросочетании
4.Задача о назначениях
2

План лекции
1.Алгоритм поиска в ширину в ориентированном графе
2.Понятие паросочетания
3.Задачао наибольшем паросочетании
4.Задача о назначениях
3

|
1 |
|
2 |
Данорграф = ( ,), –его вершина. |
3 |
Задача: найти всевершины графа, достижимыеиз , и построить ведущие внихпути |
4 |
Алгоритмпоискавширинуизвершины
-йшаг Вершине присваиваетсяномер1.Этавершина
помещаетсявочередь исчитаетсяпросмотренной. Вершины-концыдугсначаломв включаютсяв очередь,получаютстатуспросмотренных, нумеруются,послечеговершина получаетстатус использованнойиизочередиудаляется.
Строимдеревопоискавширину:отмечаемкорень .
Данорграф = , и множество |
. |
Задача:найтивсевершиныграфа, |
|
достижимыеизвершинмножества, |
|
ипостроитьведущиевнихпути |
|
Алгоритм поиск в ширину из множества :
проводим поиск в ширину поочередно для каждой вершины множества .
-йшаг Пустьвначалеочерединаходитсявершина. Ранееейприсвоен
номер.Обозначимчерез , ,…, . вершины,являющиеся концамидугсначаломв иещенепросмотренные.Тогдавершины, ,…, помещаютсявочередь исэтогомоментасчитаются просмотренными,авершина изочередиудаляетсяиполучает статусиспользованной.
Строимдеревопоискавширину:проводимдревесныедуги
( = ,…,).
Пример: |
|
|
|
||
|
||
|
||
|
||
|
|
|
Поискиз множества , |
|
4

План лекции
1.Алгоритм поиска в ширину в ориентированном графе
2.Понятие паросочетания
3.Задачао наибольшем паросочетании
4.Задача о назначениях
5

|
1 |
|
2 |
= ( ,)–неориентированныйграф |
3 |
|
4 |
Произвольноемножество,состоящееизпопарно |
Паросочетание |
|
несмежныхреберграфа |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Примеры паросочетаний: |
|
Примеры паросочетаний: |
|||||||
{ |
},{ , }, { |
, },{ |
, |
, } |
|
{ },{ }, { , |
},{ , } |
||
|
|
|
|
|
|
|
|
|
|
6
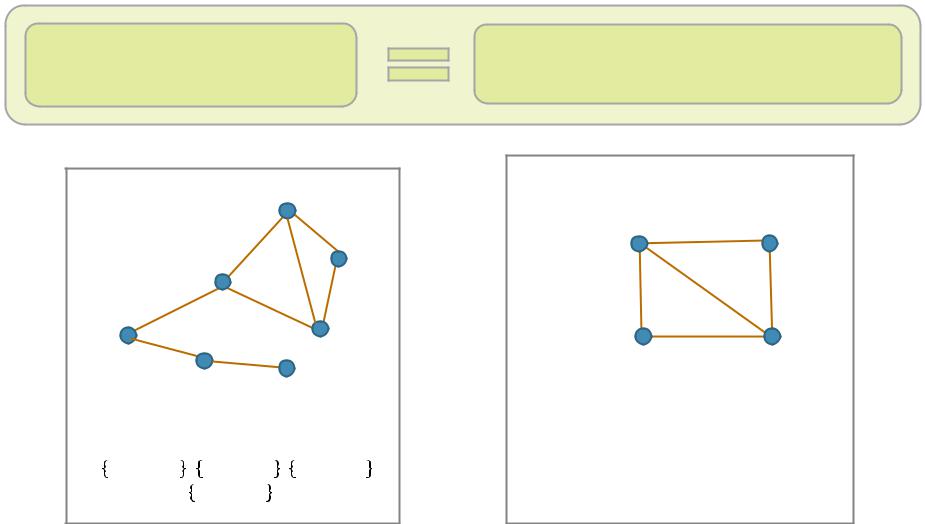
Наибольшее
паросочетание
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Наибольшиепаросочетания: |
|||||||||
|
, |
, |
, , |
, |
, |
|
, |
, , |
|
|
|
|
|
, |
, |
… |
|
|
|
Паросочетаниеснаибольшимчисломребер
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Наибольшиепаросочетания:
{ , }{ , }
1
2
3
4
7

Максимальное
паросочетание
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Максимальныепаросочетания:
, , , , ,{ , , }
Паросочетание,котороенесодержитсяв паросочетаниисбольшимчисломребер
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Максимальныепаросочетания:
{ }{ , }{ , }
Всякоенаибольшеепаросочетаниеявляетсямаксимальным, нонекаждоемаксимальное-наибольшее
1
2
3
4
8

Совершенное |
|
Паросочетание,покрывающеемножествовершин |
|
графа(каждаявершинаграфаинцидентнаодномуиз |
|
паросочетание |
|
|
|
||
|
реберпаросочетания) |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Совершенныхпаросочетаний нет
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Соверешенныепаросочетания:
{ , }{ , }
1
2
3
4
9

1.Пусть имеется рабочих, каждый из которых может выполнить один или несколько из видов работ. Работы распределяютмеждуисполнителями, соблюдаяпринцип: каждому рабочему - не более одной работы, каждой работе - не более одного исполнителя. Требуется так распределить работы между рабочими, чтобы наибольшееколичествоработбыловыполнено.
2.Пусть в предыдущей задаче число рабочих и число работ одинаково и равно . Спрашивается, можно ли так распределить работы между рабочими, чтобы были выполненывсевидыработ?
3.Пусть в дополнение к условиям второй задачи для
каждой пары рабочий-работа известна стоимость, выполнения рабочим работы . Требуется так подобрать каждому рабочему определенный вид работы, чтобысуммарнаястоимостьвыполнениявсехработбыла минимальна.
Математическаямодель
Определим двудольный граф ( ,) следующимобразом:
(1) множество вершин образуем из множестварабочих = { , ,…, } имножествавидовработ =
{ , ,…, } ( = , и будем считатьдолями);
(2) множество ребер составим из пар таких, что рабочий может выполнятьработу .
Пусть – паросочетание в построенномграфе ( ,).
Тогда каждое ребро = можно трактовать как назначение рабочему работы .
1
2
3
4
1.Требуется найти наибольшее паросочетание.
2.Требуется выяснить, существует или нет совершенное паросочетание на графе (при дополнительном
условии = )
3. Каждому ребру двудольного графа приписывается вес, равный стоимости выполнения исполнителем соответствующей работы.
Требуется найти совершенное паросочетание с минимальным весом.
10
