
Презентации лекций / Презентация лекции 13 ДМ 20
.pdf
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
1 |
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
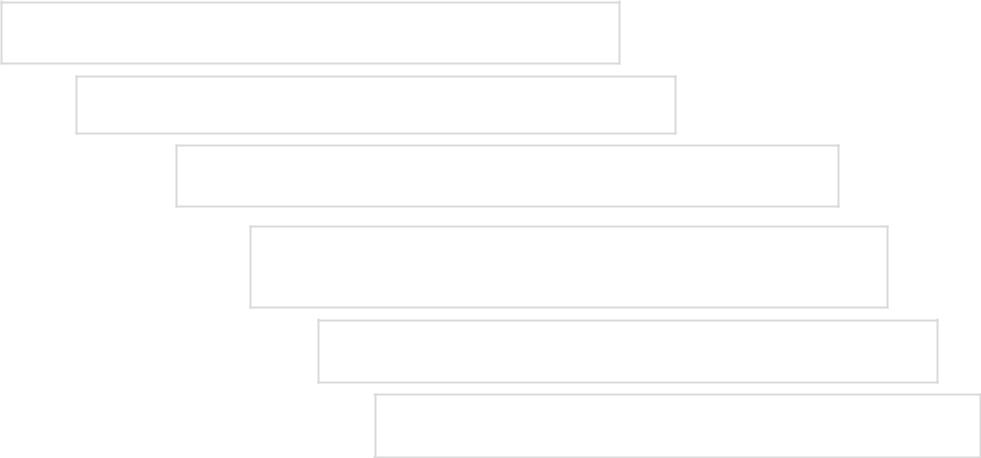
Чтообязательносовпадаету изоморфныхорграфов?
Уних одинаковоечисло вершин.
Уних одинаковоечисло дуг.
Уних одинаковыйнабор полустепенейисхода,полустепеней захода,степеней вершин.
Уних одинаковоечисло петель.
Уних одинаковоечисло пар симметричныхи параллельных дуг.
……………………………………..
1
2
3
4
5
6
11
План лекции
1. Понятие ориентированного графа
2.Изоморфные орграфы
3.Матрицы смежности и инцидентности
4.Ориентированные пути, циклы и цепи на орграфе
5.Ориентированные деревья
6.Отыскание кратчайших путей
1
2
3
4
5
6
12
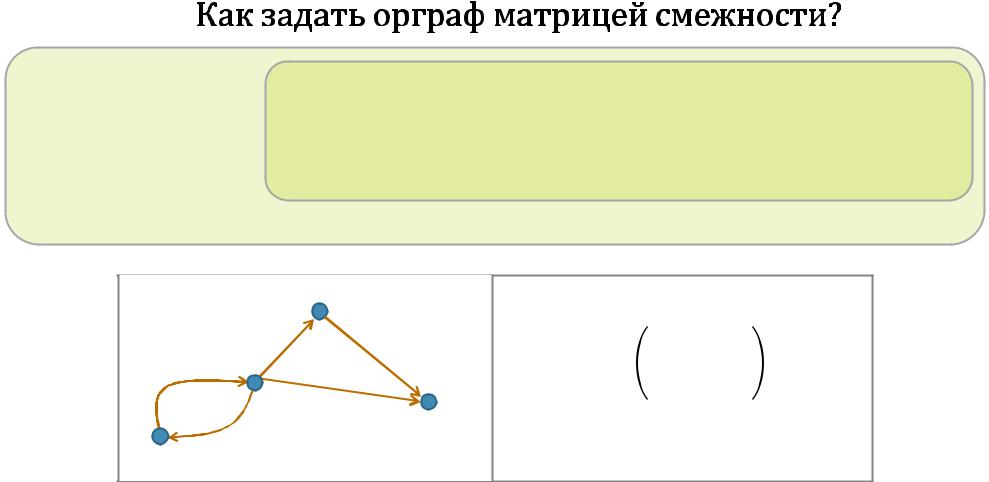
Нумеруем вершины |
Записываемматрицу размера × , в которой |
|
элемент, стоящийнапересечении -й строкии -гостолбца, |
||
орграфа: |
||
равенчислудуг, |
||
1,2,3,…, |
||
выходящихиз вершины сномером и входящихввершинус номером . |
||
|
||
|
Получаемматрицусмежностиграфа. |
Пример:
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
2 |
|
= |
||||
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
4 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
2
3
4
5
6
Чтоизменится,еслииначезанумероватьвершины? |
|
Матрицасмежностизадает графс точностьюдо изоморфизма. |
13 |
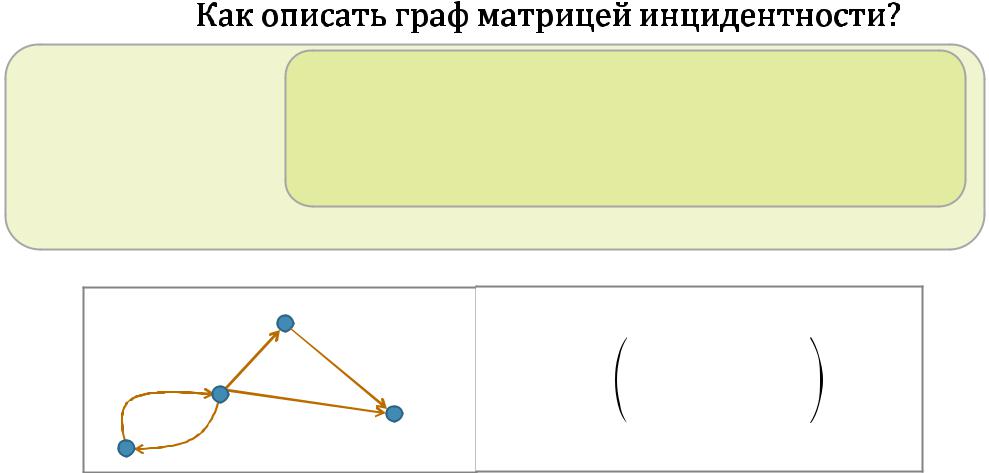
Нумеруем вершины |
Записываемматрицу размера × сэлементами , , вкоторой: |
||
(1) , |
= 1 , есливершина с номером - началодуги с номером |
||
орграфа:1,2,3,…, . |
|||
|
и -я дуга не петля, |
||
Нумеруем дугиорграфа: |
|
||
(2) , |
= −1 , есливершина с номером - конец дуги с номером |
||
1,2,3,…, . |
|||
|
и -я дуга не петля, |
||
|
|
||
|
(3) , |
= 0 в остальныхслучаях. |
|
|
|
Получаемматрицуинцидентностиорграфа. |
|
Пример:
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
−1 |
0 |
0 |
0 |
|
|
|
|
−1 |
1 |
1 |
1 |
0 |
|
|
2 |
|
|
||||||
|
|
|
= 0 |
0 |
−1 |
0 |
1 |
||
|
|
|
|
||||||
|
|
|
|
4 |
0 |
0 |
0 |
−1 |
−1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
2
3
4
5
6
Чтоизменится,еслииначезанумероватьвершиныиребра?
Еслинет петель,томатрицаинцидентностизадает орграф сточностьюдоизоморфизма. 14
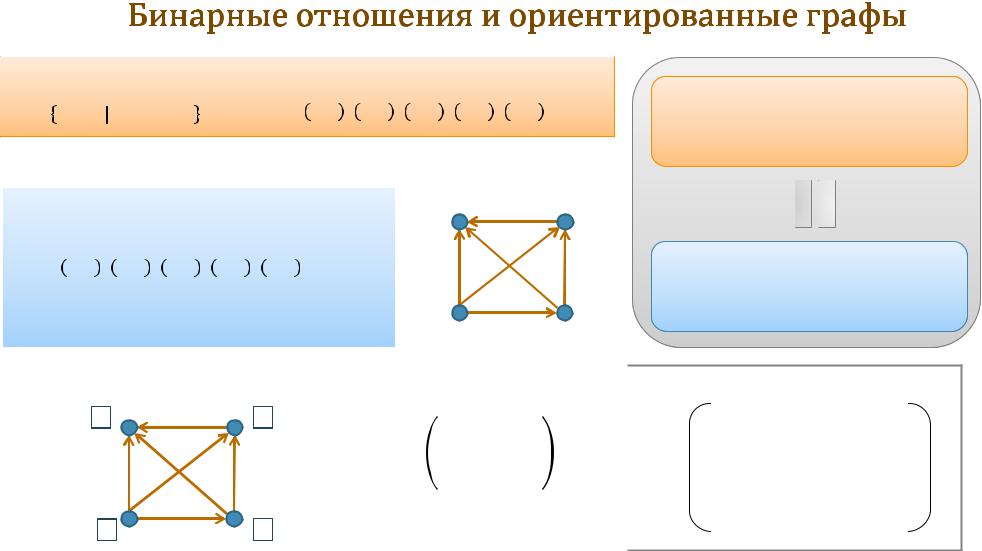
Бинарноеотношениена множестве = {5,6,8,9}:
= ( , ) ≥ +1 , или = { 6,5 , 8,5 , 8,6 , 9,5 , 9,6 ,(9,8)}
Опишембинарноеотношениекак ориентированныйграф ( , ):
|
|
|
|
|
|
|
|
5 |
|
|
6 |
|
|
|
= {5,6,8,9} – множествовершинграфа |
|
|
|
|
|
|
|
|
||||
|
= { 6,5 , |
8,5 , 8,6 , |
9,5 , 9,6 ,(9,8)} – |
|
|
|
|
|
|
|
|
||
|
множестводуг графа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
Диаграмма ( ,) |
|
|
Матрицасмежности: |
|
|
|
||||||
|
51 |
|
|
62 |
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
= |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
94 |
|
|
83 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
2
3 4 5
Бинарноеотношениена 6 конечноммножестве
Ориентированныйграф безпараллельныхдуг
Матрицаинцидентности:
-1 |
-1 |
-1 |
0 |
0 |
0 |
= 1 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
1 |
-1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
15
План лекции
1. Понятие ориентированного графа
2.Изоморфные орграфы
3.Матрицы смежности и инцидентности
4.Ориентированные пути, циклы и цепи на орграфе
5.Ориентированные деревья
6.Отыскание кратчайших путей
1
2
3
4
5
6
16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
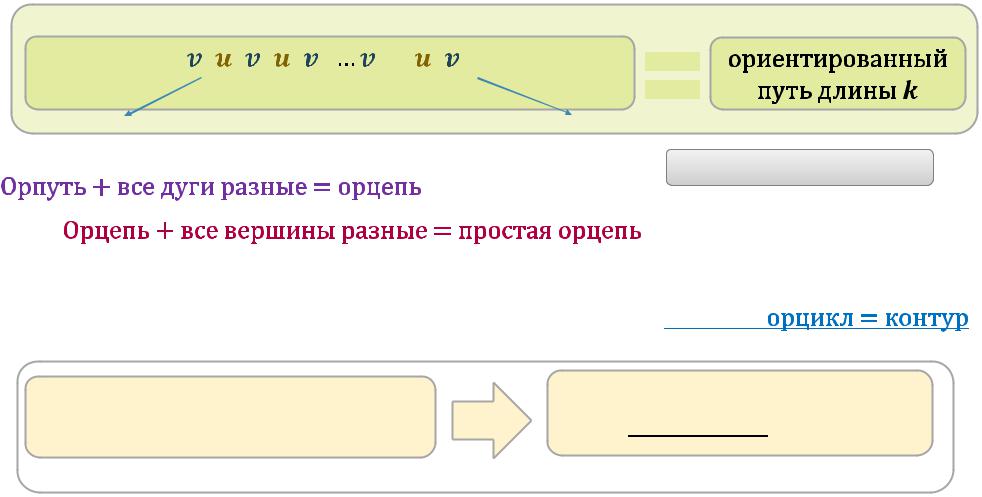
, |
…, – вершины |
|
|
|
|
,…, |
– дуги |
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= ( |
|
, ) |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– началоориентированногопути |
|
|
|
– конец ориентированногопути |
|
||||||||||
вершина– орпутьдлины 0
 допускается =
допускается =


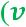













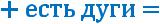

Наорграфеестьориентированный |
Награфе естьориентированная |
путьиз в |
простаяцепьиз в |
Леммао простойориентированнойцепи
17
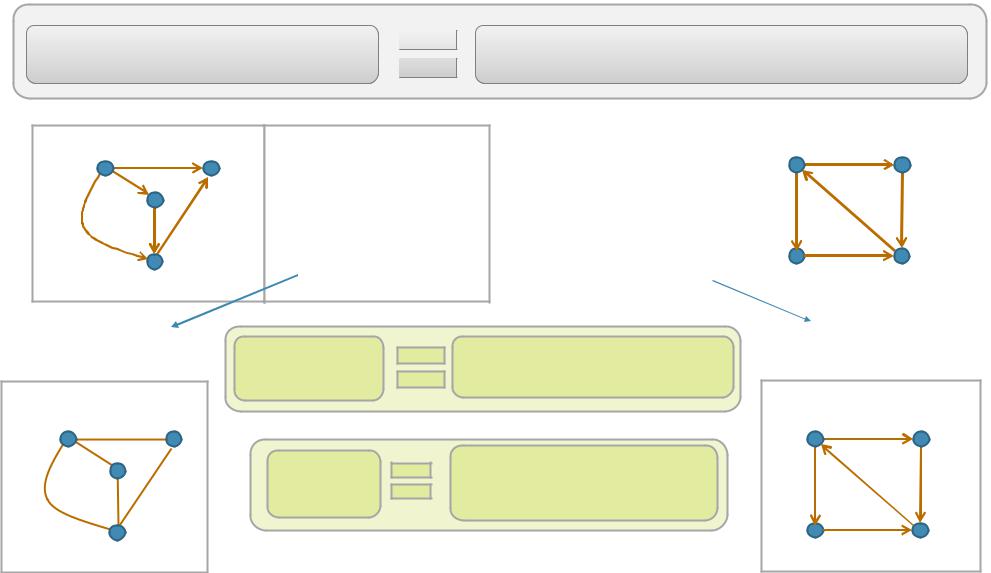
Вершина достижимаизвершины
|
|
2 |
|
|
|
|
|
|
достижима из |
|
|
|
достижима из |
|
|
|
5 |
|
|
|
|
|
достижима из , , |
|
|
|
4 |
3 |
|
|
1 |
достижима из , |
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
Существуюториентированныйпутьиз в |
3 |
||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||
достижима из ,,, |
|
|
|
|
|
|
|
достижима из ,,, |
|
|
|
|
|
|
|
достижима из ,,, |
|
|
|
|
|
|
|
достижима из ,,, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не сильно связный |
Орграф |
Любаявершинаграфа |
сильно связный |
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
сильносвязен |
достижимаизлюбойдругой |
- связное основание |
|
||
|
- связное основание |
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Основаниеграфа– |
|
|
|
|
||
|
|
5 |
|
Орграф |
|
|
|
|
|
|
|
3 |
связный |
|
|||||
|
|
4 |
связен |
|
|
|
|
||
|
1 |
неориентированныйграф |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
связный орграф |
|
|
18 |
||||
|
|
|
|
|
связный орграф |
||||
План лекции
1. Понятие ориентированного графа
2.Изоморфные орграфы
3.Матрицы смежности и инцидентности
4.Ориентированные пути, циклы и цепи на орграфе
5.Ориентированные деревья
6.Отыскание кратчайших путей
1
2
3
4
5
6
19
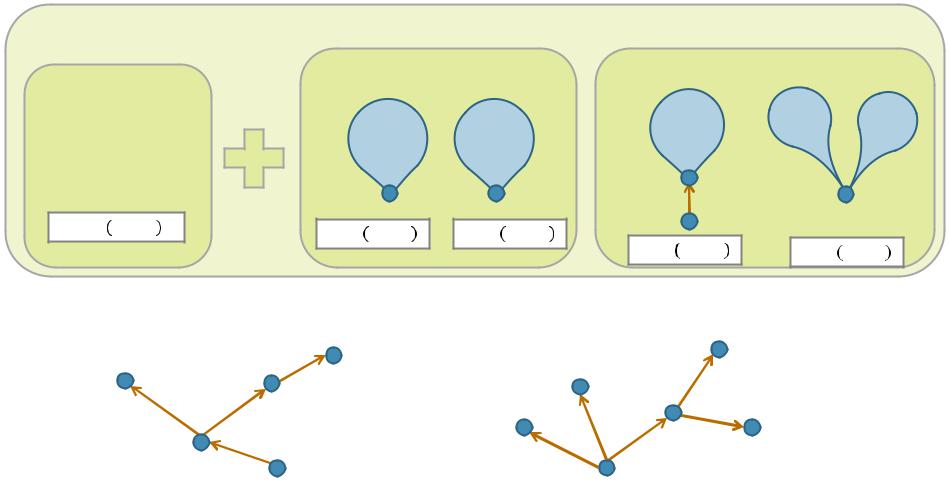
Базис индукции:

Ордеревобез дуг
иодной вершиной
-корнем
= ,
Ориентированное дерево
Индуктивный переход:
|
Пусть |
и |
-ордеревья |
Тогда |
и -ордеревья |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||
|
|
|
|
|
|
|
|
|
= , |
|
|
= , |
|
|
|
|
|
|
|
||||
|
|
|
|
|
= , |
= |
, |
1
2
3
4
5
6
корень |
корень |
20 |
|
|
