
Презентации лекций / Презентация лекции 12 нов
.pdf
Тема 12 «Обходы графов. Раскраска графов»
«Дискретная математика» Олейник Татьяна Анатольевна
кафедра ВМ-1
План лекции
1.Эйлеров цикл и эйлерова цепь
2.Гамильтонов цикл и гамильтонова цепь
3.Раскраска вершин графов
4.Раскраска граней плоских графов
2
План лекции
1.Эйлеров цикл и эйлерова цепь
2.Гамильтонов цикл и гамильтонова цепь
3.Раскраска вершин графов
4.Раскраска граней плоских графов
3
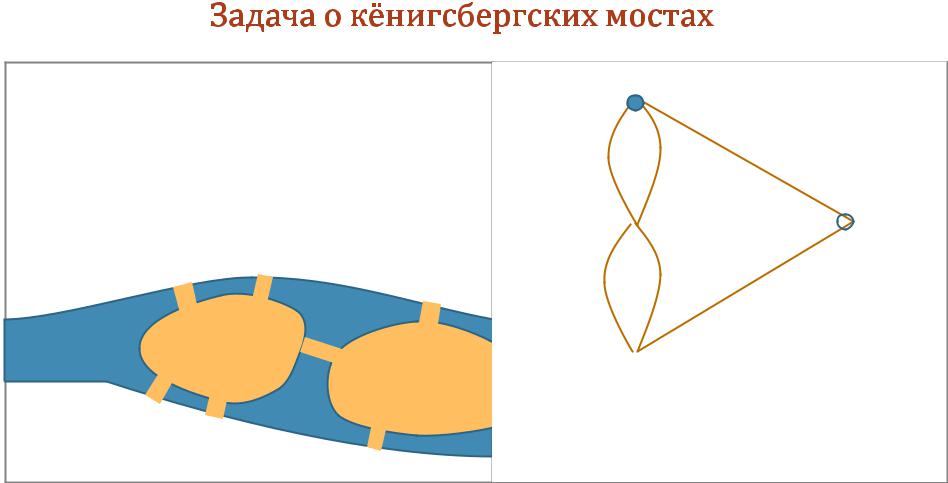
Во времена Эйлера на реке Прегельв Кёнигсберге было семь мостов, соединяющие берега реки и два острова так, как изображено на рисунке.
Можно ли выйти из дома и вернуться обратно, пройдя в точности один раз по каждому мосту?
C
А
D
B
1
2
3
4
C
D
A 

B 
Эйлер свел задачу к поиску цикла, содержащего все ребра графа
Попробуем найти такой цикл… Не получается... |
Почему? |
|
4 |
|
|
|
|
|
|
|
1 |
|
Циклнаграфе, |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
Эйлеровцикл |
3 |
||||
содержащийвсевершиныиребраграфа |
|
|
|
|||||
|
|
|||||||
|
|
|
|
|
|
4 |
||
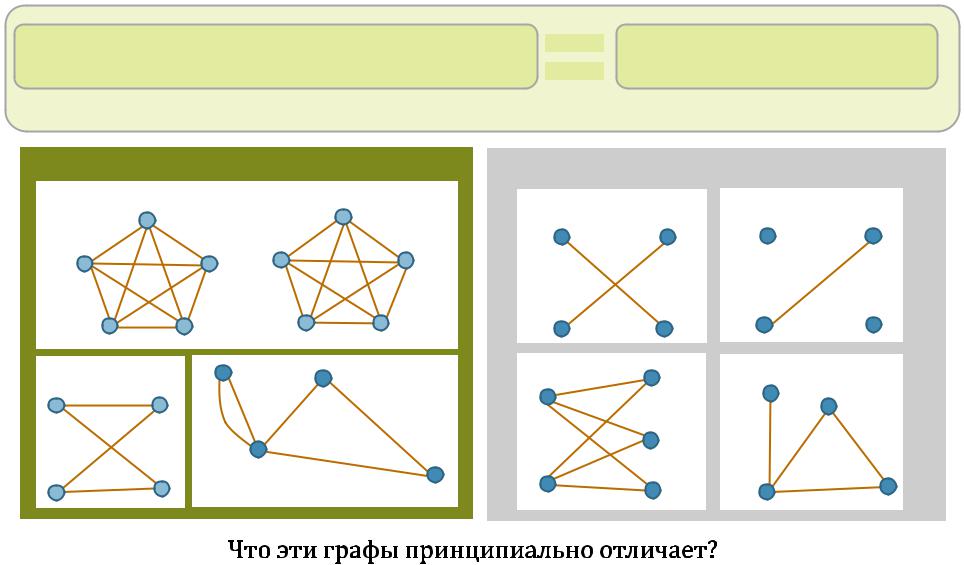
Граф,на котороместьэйлеровцикл,называют эйлеровымграфом |
||||||||
|
||||||||
На этих графах есть эйлеров цикл |
Эти графы не имеют эйлеровых циклов |
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
, |
|
5

1
2
3
4
Граф содержит эйлеров |
Каждая вершина графа имеет |
цикл |
четную степень |
6

|
1 |
|
2 |
Цепьнаграфе, |
3 |
содержащаявсевершиныиребраграфа, |
4 |
–эйлеровацепь |
|
Граф содержит эйлерову |
|
|
Граф имеет не болеедвух |
||
цепь |
|
|
|
вершин нечетной степени |
|
|
к |
н |
, |
к |
|
|
|||||
|
|
|
|
|
|
н |
к |
н |
|
7 |
|||
|
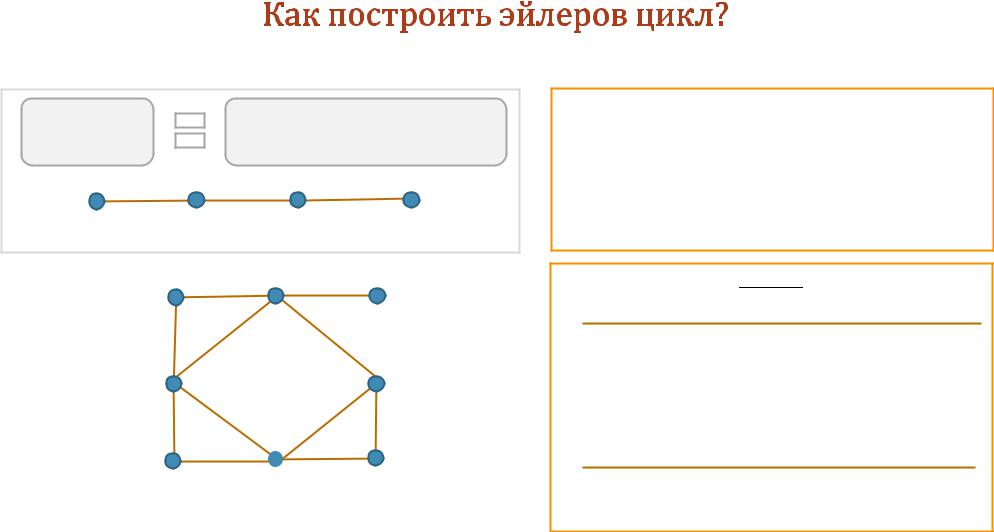
-перешеек
− имеетбольшененулевых компонентсвязности,чем
- перешеек, |
, - нет |
1 6
12 |
2 |
5 |
7 |
|
|
||
|
|
|
|
|
|
|
|
11 3 4 8
10  9
9
1,2,3,4,5,6,7,8,9,10,11,12 – эйлеров цикл
1
2
3
АлгоритмФлери 4
1-й шаг
Произвольновыбираемвершину и инцидентноеей ребро(дадим емуномер1). Переходимпо нему ввершину , после чего реброудаляем.
-й шаг
Находимсяввершине .
Выбираеминцидентноеей ребро, соблюдаядваусловия:
1) при наличиевыбораэто не должнобыть ребросконцом
2) ребронедолжнобыть перешейком.
Даемвыбранномуребруномер , проходимпо нему из в , после чегореброудаляем
8
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
|
|
|
|
|
|
|
|
|
|
АлгоритмФлери |
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
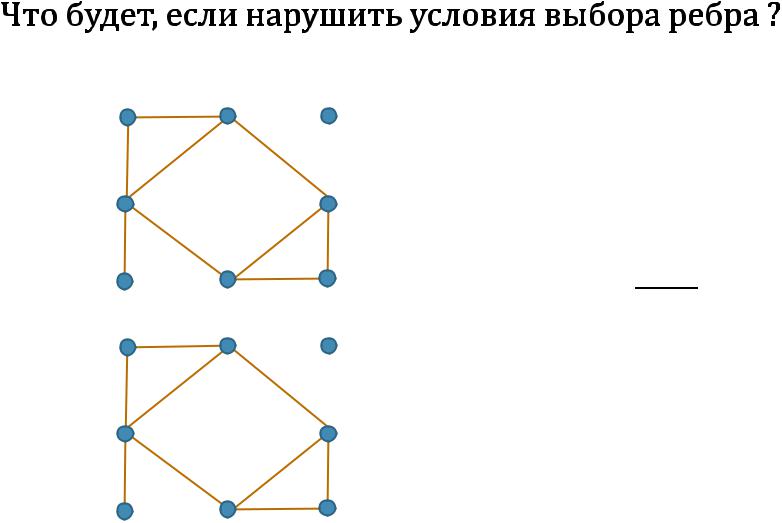
Нарушаем |
|
1 |
|
|
|
|
|
|
|
1-й шаг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условие 1) |
|
|
|
|
|
|
|
|
|
Произвольновыбираемвершину |
и |
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
инцидентноеей ребро(дадим емуномер1). |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Переходимпо нему ввершину , после чего |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
реброудаляем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-й шаг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Находимсяввершине . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нарушаем |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выбираеминцидентноеей ребро, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
условие 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соблюдаядваусловия: |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
|
|
|
5 |
4 |
|
|
1) при наличиевыбораэто не должнобыть |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ребросконцом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
2) ребронедолжнобыть перешейком. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даемвыбранномуребруномер , проходимпо |
|
||||
|
|
|
|
|
|
|
|
|
|
нему из в , после чегореброудаляем |
|
||||
|
|
|
7 |
|
|
|
|
|
|
9 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
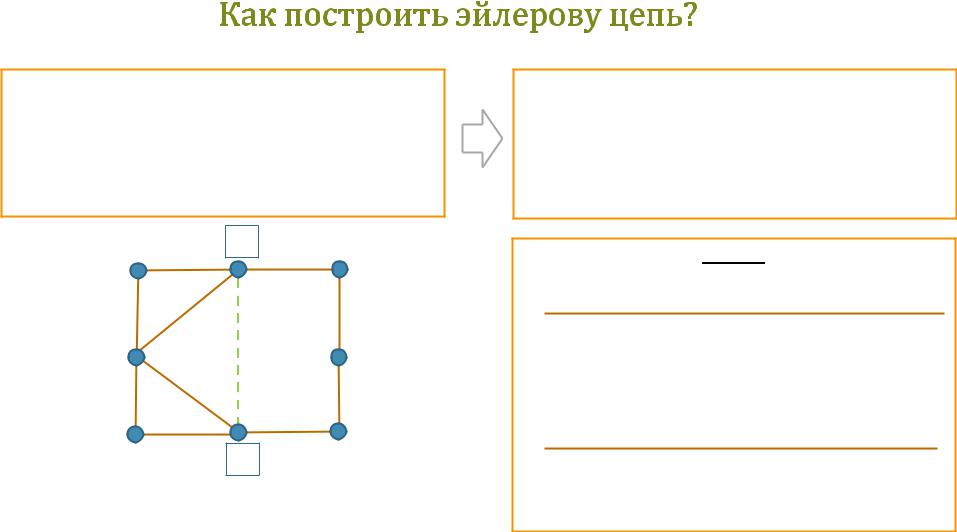
0-й шаг
Соединяемребром двевершины нечетной степени и .
|
|
9 |
2 |
8 |
3 |
10 |
|
1
11
7 4
6 |
5 |
|
|
1-е ребро в цепь не записываем
2,3,4,5,6,7,8,9,10,11 – эйлерова цепь
1
2
3
4
1-й шаг
Из вершины переходим поребру (дадим ему номер 1) ввершину , после чегоребро удаляем.
-й шаг
Находимсяввершине .
Выбираеминцидентноеей ребро, соблюдаядваусловия:
1) при наличиевыбораэто не должнобыть ребросконцом
2) ребронедолжнобыть перешейком.
Даемвыбранномуребруномер , проходимпо нему из в , после чегореброудаляем
10
