
Презентации лекций / Презентация лекции 7 ДМ 20
.pdf
Тема 7 «Полнота системы булевых
функций»
«Дискретная математика» Олейник Татьяна Анатольевна
кафедра ВМ-1

План лекции
1. Понятие о полноте системы булевых функций
2. Критерий полноты Поста |
|||
О |
|
о функции,не сохраняющей0 |
|
б |
|
||
о |
|
офункции,не сохраняющей1 |
|
с |
|
||
н |
Леммы |
онесамодвойственнойфункции |
|
о |
|||
о немонотоннойфункции |
|||
в |
|
||
а |
|
о нелинейнойфункции |
|
н |
|
||
и |
Доказательствосамогокритерия |
||
е |
|||
|
|
2 |
|

План лекции
1. Понятие о полноте системы булевых функций
2. Критерий полноты Поста |
|||
О |
|
о функции,не сохраняющей0 |
|
б |
|
||
о |
|
офункции,не сохраняющей1 |
|
с |
|
||
н |
Леммы |
онесамодвойственнойфункции |
|
о |
|||
о немонотоннойфункции |
|||
в |
|
||
а |
|
о нелинейнойфункции |
|
н |
|
||
и |
Доказательствосамогокритерия |
||
е |
|||
|
|
3 |
|
Множество булевыхфункций
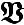


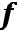

 -полнаясистема,
-полнаясистема,
еслилюбаябулевафункцияможет быть заданаформулойнад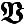

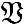 -полнаясистема,если
-полнаясистема,если
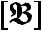


Примеры:
Задаем функцию |
|
Задаем функцию |
|
Задаем функцию |
|
|
|
в виде СДНФ или СКНФ, |
|||
|
|
|
|||
? в виде СДНФ или СКНФ |
? |
в виде СДНФ или СКНФ, |
? |
||
используем закон де Моргана |
|||||
используем закон де Моргана |
|||||
|
|
|
|||
|
|
|
|
1
2
4
1
2
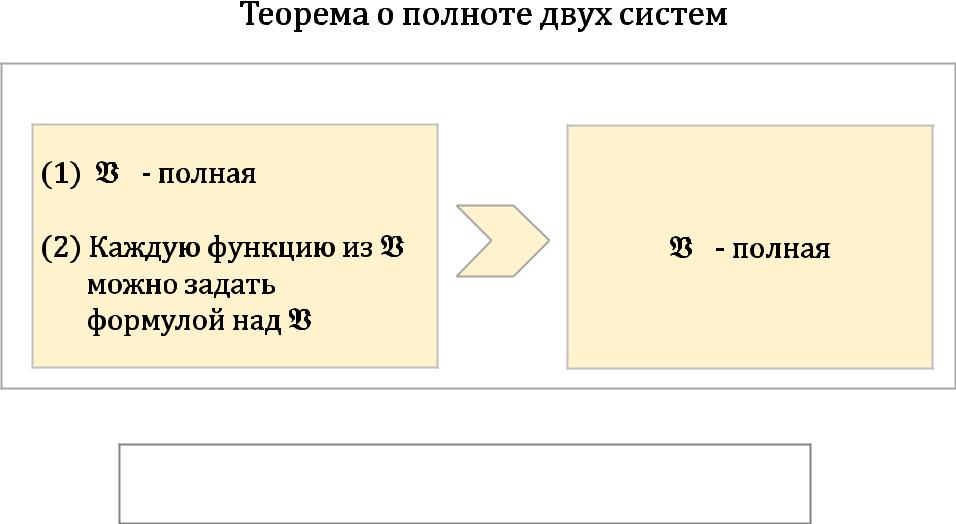
Естьдвесистемы функций = { , ,…} и |
= { , |
,…} |
|
|
|
|
|
|
|
|
|
|
|
|
|
Важно! |
Теорема–достаточноеусловиеполноты. |
|
|
|
Используятеорему,доказатьнеполнотунельзя! |
|
|
5

План лекции
1. Понятие о полноте системы булевых функций
2. Критерий полноты Поста |
|||
О |
|
о функции,не сохраняющей0 |
|
б |
|
||
о |
|
офункции,не сохраняющей1 |
|
с |
|
||
н |
Леммы |
онесамодвойственнойфункции |
|
о |
|||
о немонотоннойфункции |
|||
в |
|
||
а |
|
о нелинейнойфункции |
|
н |
|
||
и |
Доказательствосамогокритерия |
||
е |
|||
|
|
6 |
|
1
2
|
Естьсистемафункций = { , ,…} |
Важно! |
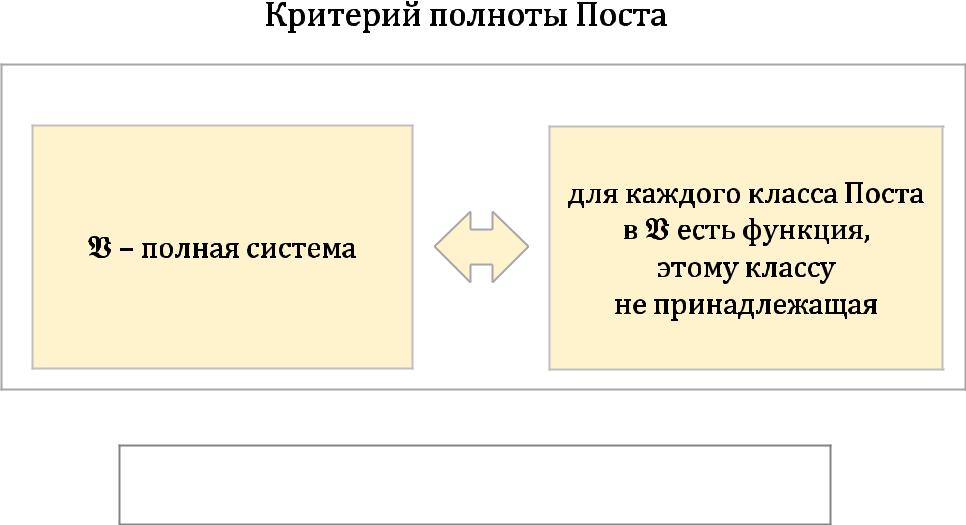
Критерий–необходимоеи достаточноеусловиеполноты. |
|
Используякритерий,можнодоказатькакполноту, |
|
такинеполнотусистемы! |
|
7 |

1
2
|
|
|
|
Классы Поста |
|
|
|
Классы Поста |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
− |
|
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
− |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
… |
|
|
|
− |
|
|
… |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
− |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Вкаждомстолбцеестьминус |
|
|
Естьстолбецизодних«+» |
|
||||||||
|
|
Система = { , ,…} полная |
Система = { , ,…} неполная |
|
|||||||||
|
|
Задача. Выяснить, полны ли системы функций: (1) |
0,1, |
, , ; |
(2) {→, |
, |
}. |
8 |
|||||
1
2
= { , ,…}–полная |
|
|
|
послеудаленияиз любой |
|
|
|
||
|
|
|
функцииполнотатеряется |
|
|
|
|
||
|
|
|
|
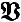

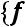

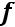


 - базис
- базис
дизъюнктивный |
базис |
|
конъюнктивный |
базис |
базисПирса |
базис |
|
|
Шеффера |
|
|
|
|
|
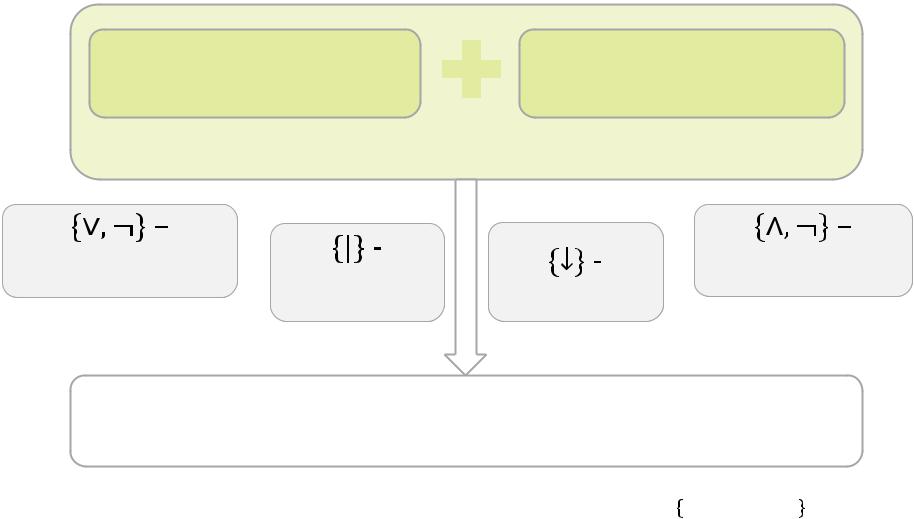
Есливполнойсистеме = { , ,…} естьфункция, после удалениякоторойполнотанетеряется, то – не базис.
Задача. Выделить все базисы из полной системы функций 0,1, , , .
9

Пусть .Тогдаформулойнадмножеством можнозадать константу или¬.
Нужнаяформулаимеетвид:
( ,,…,)
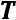
Примеры:
1) ( , ) = (1000)
Нужнаяформула:,
, = ( ) = ̅
обозначим
2) ( , ) = (1001)
Нужнаяформула: g ,
, = ( ) = 1
обозначим
О
б
о
с
н
о
в
а
н
и
я
10
