Презентации лекций / Презентация лекции 1 ДМ 20
.pdf
Тема 1 «Множества и бинарныеотношения»
«Дискретная математика» Олейник Татьяна Анатольевна
кафедра ВМ-1
План лекции
1.Множестваи |
|
|
|
|
|
операции над |
|
2. Бинарные |
ними |
|
|
|
отношения на |
|
|
|
|
|
|
множестве |
|
||
|
|
|
2
План лекции
1.Множестваи |
|
|
|
|
|
операции над |
|
2. Бинарные |
ними |
|
|
|
отношения на |
|
|
|
|
|
|
множестве |
|
||
|
|
|
3
Множество– совокупностьразличных
объектов
,,
«элементов»
,
количествоэлементовможет быть:
конечным бесконечным нулевым
конечноемножество |
бесконечноемножество |
пустое множество |
|
|
|
|
|
Число элементов множества
- его мощность
1
2
4
1
2
Каждый элемент естьэлемент |
подмножество |
- подмножестволюбогомножества Если и ≠ ,то -собственное подмножество . Пишут
и |
и равны |
=
Множествовсехподмножеств |
булеан |
5
Операции над множествами
Название операции |
Определениеоперации |
Объединение
и 
Пересечение
и
Разность 
и 
Дополнение 
Декартово произведение
и 
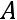
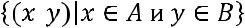
1
2
Операцииобъединения,пересечения,декартовапроизведения |
|
обобщаютсяна любоеконечноечисломножеств |
6 |
коммутативные законы: |
|
1 |
1. A B B A ; |
2. A B B A ; |
2 |
ассоциативные законы: |
|
|
3.A B C A B C ;
4.A B C A B C ;
дистрибутивные законы:
5.A B C A B A C ;
6.A B C A B A C ;
законы идемпотентности: |
|
|
|
|
|
|
|
|
|
|||||||||||
7. A A A ; |
8. A A A ; |
|||||||||||||||||||
законы де Моргана: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
9. |
A B |
A |
B |
; |
10. |
A B |
A |
B |
||||||||||||
законы нуля: |
|
|
|
|
|
|
|
|
|
|||||||||||
11. |
|
A A; |
12. |
A ; |
||||||||||||||||
законы единицы: |
|
|
|
|
|
|
|
|
|
|||||||||||
13. |
|
A I I ; |
14. |
A I A ; |
||||||||||||||||
законы поглощения: |
|
|
|
|
|
|
|
|
|
|||||||||||
15. |
|
A A B A; |
16. |
A A B A; |
||||||||||||||||
законы дополнения: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
A |
|
I ; |
|
A |
|
; |
||||||||||||
17. |
A |
18. |
A |
|||||||||||||||||
закон двойного дополнения: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||
19. |
|
A |
A. |
|
7 |
|||||||||||||||
Утверждения о числе элементов конечных множеств
Между
и
существует взаимнооднозначное соответствие
1
2
конечны
|
|
|
|
|
|
8
|
1 |
Утверждения о числе элементов конечных множеств |
2 |
|
, ,…, конечны |
|
|
|
Правилосуммы |
|
||
ипопарно непересекаются |
|
|
|
|
= |
+ |
+ + |
|
|
||||||
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, ,…, конечны |
|
|
|
Формулавключений-исключений |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
− |
|
|
∩ |
|
+ |
||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
∩ |
∩ |
|
−+(− ) |
|
∩ |
|
∩ ∩ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
1
2
|
непустые |
|||||
, ,…, - |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
попарнонепересекаются |
||||||
подмножества |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
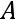разбиение
ихобъединениесовпадаетс
…
10