Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)» (МГТУ им. Н.Э. Баумана)

Кафедра СМ9 «Многоцелевые гусеничные машины и мобильные роботы»

Отчёт по лабораторной работе №4

по курсу «Динамика транспортных средств»

по теме: «Тормозной режим качения колеса»

Студент (ФИО, группа)	___________________________ (Подпись, дата)	Новиков А.Д. СМ9-71
Преподаватель	___________________________ (Подпись, дата)	Тихонов Е.А.

Москва 2023 г.

Цель работы – создание математической модели колеса автомобиля при разгоне и торможении, и реализация этой модели в ПО Matlab Simulink.

1 Расчетная схема

При создании расчетной схемы руководствуемся следующими допущениями:

1. Движение колеса прямолинейное, по твердой ровной опорной поверхности;

2. Колеса жесткие, контакт колеса с опорной поверхностью – точечный.

3. Связь колеса и опорной поверхности является удерживающей (колесо не отрывается от поверхности);

4. Положение оси колеса относительно нормали к опорной поверхности не изменяется;

Н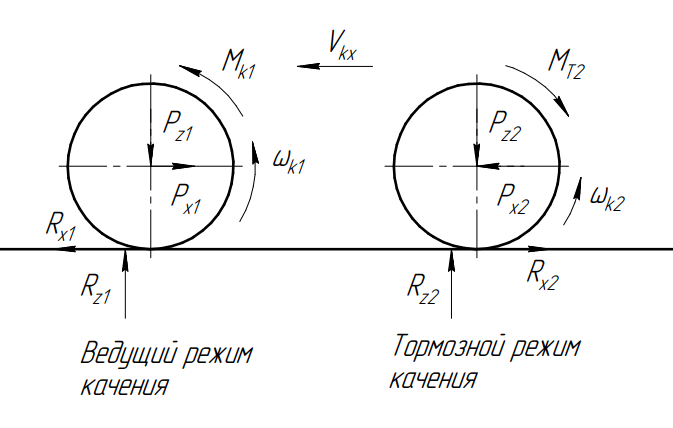 а рисунке 1 изображена расчетная схема, рассматриваемая в данной лабораторной работе.

Рисунок 1 – Расчетная схема для колеса в различных режимах качения

– текущая горизонтальная скорость движения колеса, ;

– угловые скорости вращения колес, ;

– крутящий момент, ;

– тормозной момент, ;

– внешняя продольная сила, ;

– внешняя вертикальная сила, ;

Запишем уравнение движения для колеса:

(1)

где 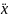– ускорение центра масс колеса, ;

– масса четверти автомобиля, приходящаяся на одно колесо, и колеса, кг.

– продольная реакция в пятне контакта колеса с опорной поверхностью, ;

– коэффициент сцепления колеса с опорной поверхностью;

– константы, определяющие форму кривой коэффициента сцепления;

– вертикальная сила реакции со стороны опорной поверхности, ;

– момент инерции колеса относительно оси его вращения, ;

− динамический радиус колеса, ;

– угловая скорость колеса, ;

– крутящий момент, подводимый к колесу от трансмиссии, ;

– момент сопротивления качению, ;

– коэффициент сопротивления качению;

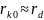− радиус чистого качения, м;

− ускорение свободного падения, .

Будем считать зависимость крутящего момента на колесе от угловой скорости линейной, как указано на рисунке 2.

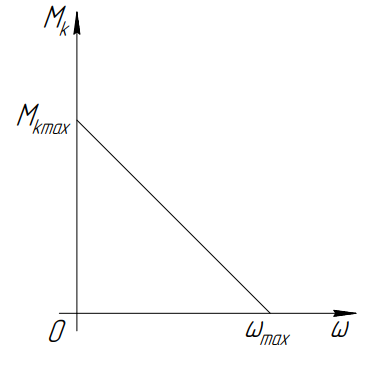
Рисунок 2 – Зависимость от

(2)

Коэффициент скольжения меняет свой знак в зависимости от режима качения колеса: − соответствует тяговому режиму, – тормозному, поэтому используем обобщенную формулу для различных режимов, тогда коэффициент скольжения определяется формулой (2).

Д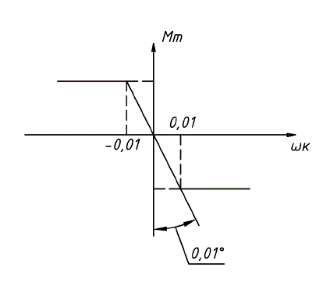 ля получения тормозного момента построим график зависимости от угловой скорости колеса . Для учета возможности возникновения нежелательных рывков модели добавим небольшой наклон графика в области нуля угловой скорости. Описанный график показан на рисунке 3.

Рисунок 3 – Зависимость тормозного момента от угловой скорости колеса

Примем, что максимальный тормозной момент численно равняется максимальному крутящему моменту колеса .

При расчете в среде Matlab Simulink возникает ошибка в случае полной остановки колеса, когда и , и тогда при расчете коэффициента скольжения получается ситуация неопределенного деления на ноль. Для устранения описанной проблемы необходимо задать условие, которое останавливает моделирование с помощью блока Stop, когда линейная скорость 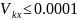. Реализация данного условия в Simulink показана на рисунке 4.

Рисунок 4 – Условие остановки расчета в Matlab Simulink

2 Исходные данные

Исходные данные для расчета в ПО Matlab представлены на рисунке 3.

Рисунок 5 – Исходные данные для расчета в Matlab

3 Тормозной режим качения колеса

В первой части лабораторной работы моделируется тормозной режим качения колеса, следовательно, .

На рисунке 6 показана математическая модель, построенная в Matlab Simulink.

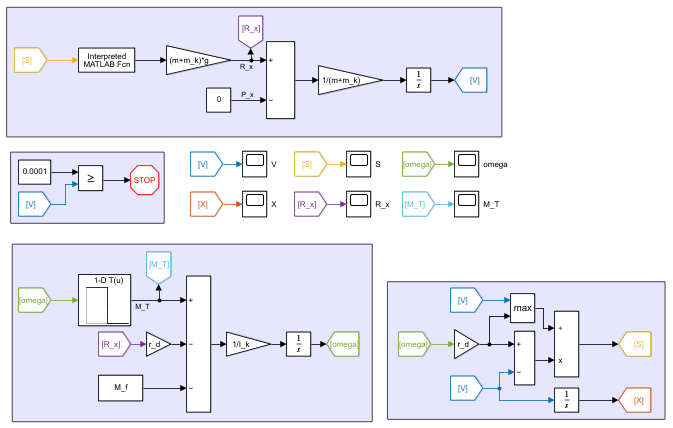
Рисунок 6 – Графическая модель для решения дифференциальных уравнений тормозного режима качения колеса

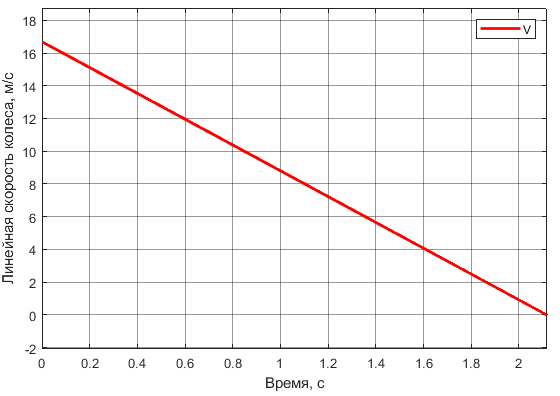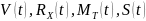Н а рисунках 7-10 показаны зависимости , соответственно.

Рисунок 7 – График изменения скорости

Рисунок 8 – График изменения продольных реакций

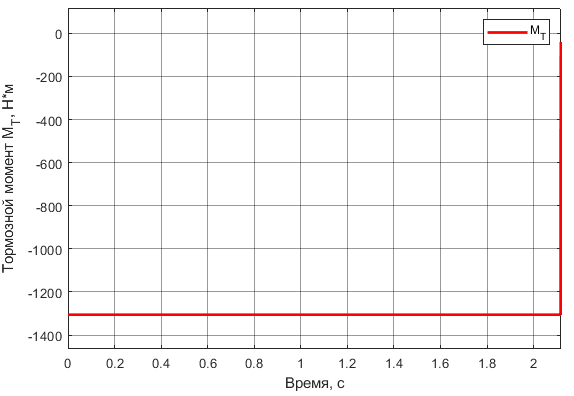
Рисунок 9 – График изменения тормозного момента

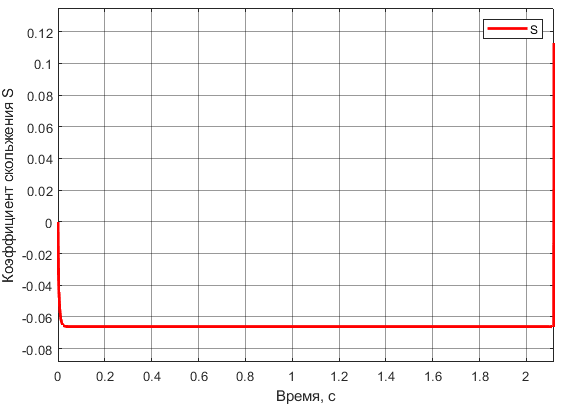
Рисунок 10 – График изменения коэффициента скольжения

4 Разгон и торможение колеса

Для переключения режимов качения колеса с разгонного (ведущего) на тормозной используем блок Switch. Пусть торможение начинается через 20 секунд. Реализация этой модели представлена на рисунке 11.

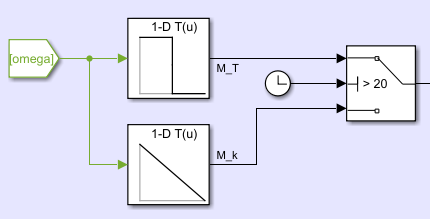
Рисунок 11 – Графическая модель переключения режимов качения колеса

На рисунке 12 показана математическая модель для решения дифференциальных уравнений, построенная в Matlab Simulink.

Рисунок 12 – Графическая модель для решения дифференциальных уравнений разгонного и тормозного режимов качения колеса

На рисунках 13-16 показаны зависимости для ведущего и тормозного режимов качения соответственно.

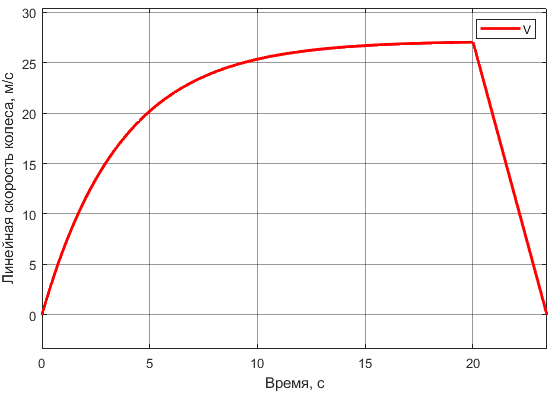
Рисунок 13 – График изменения скорости

Рисунок 14 – График изменения продольных реакций

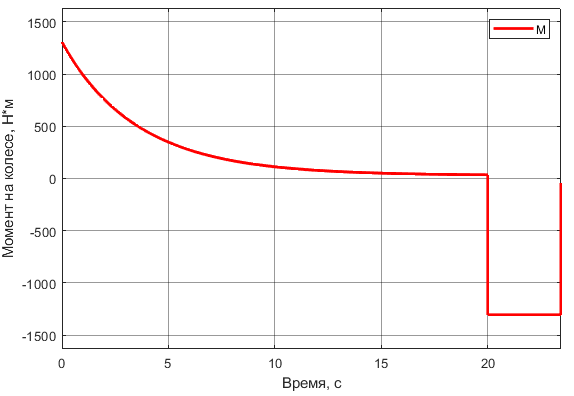
Рисунок 15 – График изменения момента на колесе

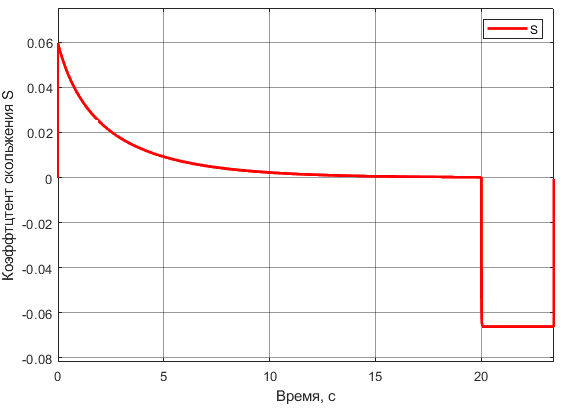
Рисунок 16 – График изменения коэффициента скольжения

5 Разгон и торможение колеса с учетом сцепления

(3)

Дополним систему уравнений (1) уравнением моментов для системы двигатель-сцепление.

где − момент инерции двигателя, ;

– частота вращения коленчатого вала, ;

– момент на коленчатом валу двигателя, ;

– момент на фрикционе, .

Будем считать зависимость момента на фрикционе от степени нажатия на педаль линейной, как указано на рисунке 17.

Рисунок 17 – График зависимости момента на фрикционе от степени нажатия на педаль сцепления

На рисунке 18 показана математическая модель для решения дифференциальных уравнений, построенная в Matlab Simulink.

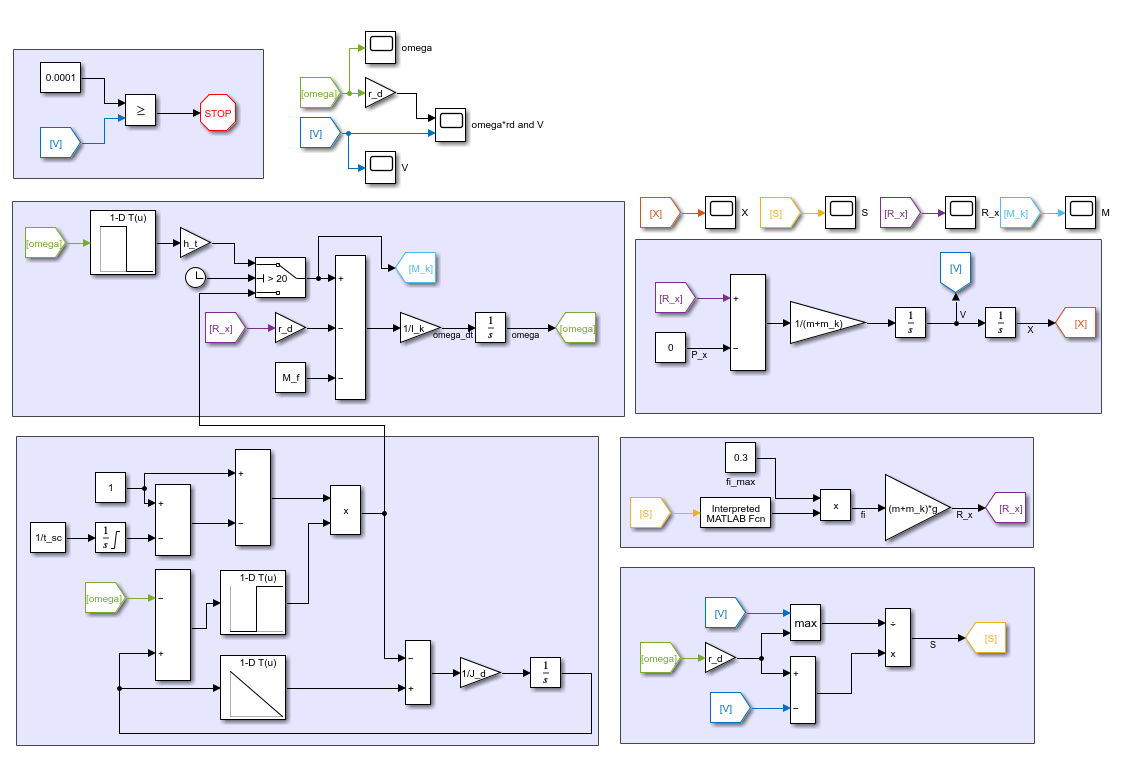
Рисунок 18 – Графическая модель разгона и торможения колеса с учетом сцепления

На рисунках 19-22 показаны зависимости соответственно.

Рисунок 19 – График изменения скоростей

Рисунок 20 – График изменения продольных реакций

Рисунок 21 – График изменения момента на колесе

Рисунок 22 – График изменения коэффициента скольжения

6 Разгон и торможение колеса с учетом сцепления и АБС

Для моделирования антиблокировочной системы с помощью блока Saturation зададим диапазон значений [0..1], в пределах которого будет изменяться дополнительный коэффициент, при умножении которого на степень нажатия педали тормоза будет получено новое скорректированное значение . Если коэффициент скольжения превышает критическое значение (происходит юз), то воздействие на педаль тормоза ослабляется для предотвращения блокировки колес.

На рисунке 23 показана математическая модель для решения дифференциальных уравнений, построенная в Matlab Simulink.

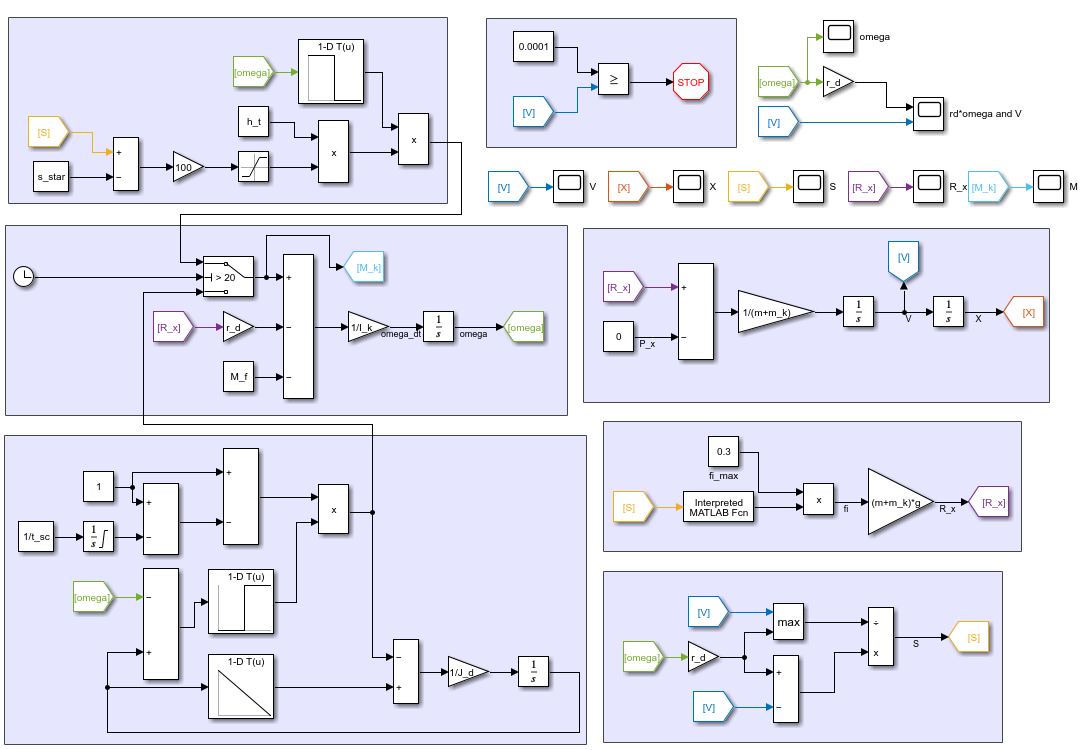
Рисунок 23 – Графическая модель разгона и торможения колеса с учетом сцепления и АБС системы

На рисунках 24, 25 показаны зависимости соответственно.

Рисунок 24 – График изменения скоростей

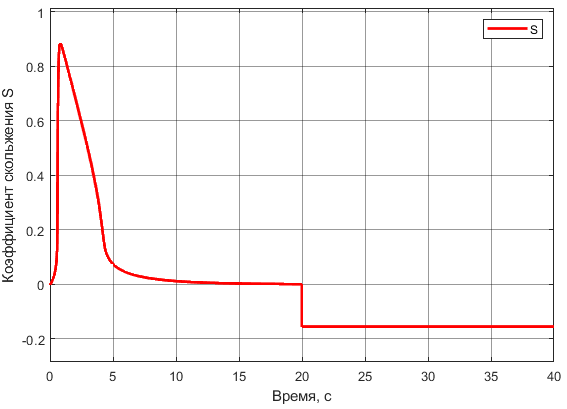
Рисунок 25 – График изменения коэффициента скольжения

7 Вывод

По результатам данной лабораторной работы была построена математическая модель тормозного и ведущего режимов качения колеса, системы сцепления и системы АБС, на основе этой модели была создана расчетная модель в ПО Matlab Simulink и получены соответствующие графические зависимости, отражающие важнейшие показатели при качении колеса в различных режимах. Из полученных графиков для последнего режима, учитывающего наличие антиблокировочной системы, видно, что данная система управляет степенью нажатия на педаль торможения и плавно уменьшает частоту вращения колеса, за счет чего повышается эффективность торможения и возрастает управляемость при торможении.