
пр 5, Гізетдінов (екон)
.docНАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ БІОРЕСУРСІВ І ПРИРОДОКОРИСТУВАННЯ УКРАЇНИ
Кафедра економетрики
Практичне заняття 5
«Емпіричні методи кількісного аналізу на основі системи статистичних рівнянь»
Виконав студент 3 курсу 1 групи
Економічного факультету
Гізетдінов Едуарт Рафікович
Київ - 2023
Завдання.
Оцінити
параметри економетричної моделі, що
характеризує
залежність між тижневими витратами на
харчування (y),
загальними
витратами (x1)
та розміром сім'ї (x2)
за формулою оператора 1МНК![]() .
Дослідити
побудовану модель, а саме:
.
Дослідити
побудовану модель, а саме:
побудувати дисперсійно-коваріаційну матрицю оцінок параметрів моделі;
знайти множинний коефіцієнт кореляції та перевірити його на суттєвість за критерієм Стьюдента;
перевірити знайдені параметри на суттєвість за критерієм Стьюдента;
побудувати інтервали довіри для знайдених параметрів;
перевірити модель на адекватність за критерієм Фішера.
Вихідні дані в умовних одиницях наведені в таблиці 1.
Варіант – 21.
Розв'язання
Запишемо економетричну модель:
![]()
![]()
де
![]() –
відповідно фактичні та розрахункові
значення тижневих витрат
на харчування за моделлю; x1
–
загальні витрати; x2
–
розмір сім'ї; и
–
залишки;
–
відповідно фактичні та розрахункові
значення тижневих витрат
на харчування за моделлю; x1
–
загальні витрати; x2
–
розмір сім'ї; и
–
залишки;
![]() –
оцінка параметрів моделі.
–
оцінка параметрів моделі.
Оператор оцінювання параметрів моделі за 1МНК має вигляд :
А = (Х'Х)-1Х'У,
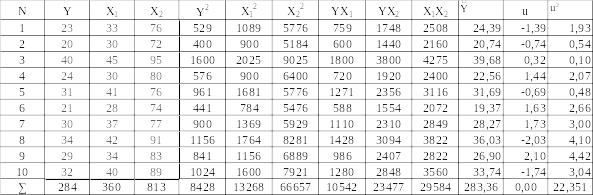
Таблиця 1.
Вхідні та розрахункові дані
Д
(23)
(20)
(40)
(24)
(31)
(21)
(30)
(34)
(29)
(32)
(1; 33; 76)
(1; 30; 72)
(1; 45; 95)
(1; 30; 80)
Х= (1; 41; 76) Y=
(1; 28; 74)
(1; 37; 77)
(1; 42; 91)
(1; 34; 83)
(1; 40; 89)
X' – матриця, транспонована до матриці X.
Матриця X, крім двох векторів незалежних змінних, містить вектор одиниць. Він дописується в цій матриці ліворуч тоді, коли економетрична модель має вільний член. Не дописуючи такого вектора одиниць, вільний член можна обчислити, скориставшись рівністю:
![]() (3), де
(3), де
![]() –
середнє значення залежної змінної;
–
середнє значення залежної змінної;
![]() ,
,
![]() –
середні значення
незалежних змінних х1,
і
х2
.
–
середні значення
незалежних змінних х1,
і
х2
.
Згідно з оператором оцінювання знайдемо
1 )(Х'Х)
=
10
360
813
)(Х'Х)
=
10
360
813
360 13268 29584
813 29584 66657
2 )
)![]() 12,652 0,076 -0,188
12,652 0,076 -0,188
0,076 0,008 -0,004
-0,188 -0,004 0,004


3)
![]() 284
284
10542
23477 (4)
4) А' = -20,34
0,76
0,26 (5).
Отже, економетрична модель має вигляд:
ŷ = -20,34+0,76х1+0,26х2 (6).
Знайдені методом 1МНК оцінки параметрів такі:
â0 = -20,34; â1 = 0,76; â2 = 0,26, тобто
 = -20,34
0,76
0,26
Отже, коли за всіх однакових умов незалежна змінна х, (загальні витрати) збільшується (зменшується) на одиницю, то залежна змінна у (оцінка витрат на харчування) також збільшується (зменшується) на 0,913 одиниць. Якщо за інших незміннних умов незалежна змінна х2 (розмір сім'ї) збільшується (зменшується) на одиницю, то залежна змінна у (оцінка витрат на харчування) також збільшується (зменшується) на 0,228 одиниць.
Для
економетричної моделі обчислимо
коваріаційну матрицю
![]() .
Отже,
маємо:
.
Отже,
маємо:
12,652 0,076 -0,188
0,076 0,008 -0,004
-0,188 -0,004 0,004
284
10542
23477
n = 10, m = 3
Обчислимо
незміщену оцінку дисперсії залишків
![]() :
:
= 22,351/10-3 = 3,193.
Визначимо дисперсії оцінок
 :
:
var(â1) = 3,193*12,652 =40,4;
var(â2) = 3,193*0,008 =0,02;
var(â3) = 3,193*0,004 =0,01.
Обчислимо коваріації відповідних оцінок параметрів:
͡σа1а2 = 3,193*0,076 = 0,24;
͡σа1а3 = 3,193*(-0,188) = -0,6;
͡σа2а2 = 3,193*(-0,004) = -0,013.
Знак
«мінус» перед оцінками коваріацій
![]() указує
на те, що
збільшення
однієї оцінки параметрів приводить до
зменшення в середньому
іншої і навпаки.
указує
на те, що
збільшення
однієї оцінки параметрів приводить до
зменшення в середньому
іншої і навпаки.
Отже, дістанемо дисперсійно-коваріаційну матрицю
var (Â) = 40,4 0,24 -0,6
0,24 0,02 -0,013
-0,6 -0,013 0,01 (10)
Запишемо стандартні помилки оцінок параметрів моделі:
Sâ1 = √40,4 =6,356;
Sâ2 = √0,02 = 0,141;
Sâ3 = √0,01 = 0,1.
Порівняємо
кожну стандартну помилку
![]() з
відповідним числовим
значенням оцінки параметра, тобто
знайдемо відношення
з
відповідним числовим
значенням оцінки параметра, тобто
знайдемо відношення
![]() (11) :
(11) :
*100 = 6,356/-20,34*100 = -0,003;
*100 = 0,141/0,76*100 = 0,002;
*100 = 0,1/0,26*100 = 0,004.
Отже, стандартні помилки оцінок параметрів щодо рівня оцінок параметрів становлять відповідно -0,003%, 0,002% і 0,004%, а це свідчить про низьку зміщеність оцінок.
Перевіримо гіпотези про значущість оцінок параметрів моделі
ŷ = -20,34+0,76х1+0,26х2,
побудованої на основі вихідних даних, наведених у табл. 1.
t1 = -20,34/6,356= -3,2;
t2 = 0,76/0,141 = 5,4;
t3 = 0,26/0,1 = 2,6.
Якщо ступінь
свободи n – m = 10 – 3 = 7
і рівень значущості
= 0,05, tтабл
= 2,16. Оскільки t1факт
< tтабл,
t2факт > tтабл,
t3факт < tтабл
то оцінки параметрів
![]() ,
,
![]() ,
,
![]() характеризують неістотний зв’язок цих
незалежних змінних (
характеризують неістотний зв’язок цих
незалежних змінних (![]() ,
,
![]() ,
,
![]() )
із залежною.
)
із залежною.
Оцінка параметра може перебувати в таких межах:
![]() ;
;
-20,34-2,16*6,356 ≤ а1 ≤ -20,34+2,16*6,356;
-34,07 ≤ а1 ≤ -6,61;
![]() ;
;
0,76-2,16*0,141≤ а2 ≤ 0,76+2,16*0,141;
0,45≤ а2 ≤ 1,06;
![]() ;
;
0,26-2,16*0,1≤ а3 ≤ 0,26+2,16*0,1;
0,044≤ а3 ≤ 0,476.
