
ПримерТ. р. №1
.docПример решения типовой расчета
Задание №1.
Даны матрицы
![]() и
и
![]() .
Найти:
.
Найти:
-
матрицы
 и
и
 ;
; -
определители матриц
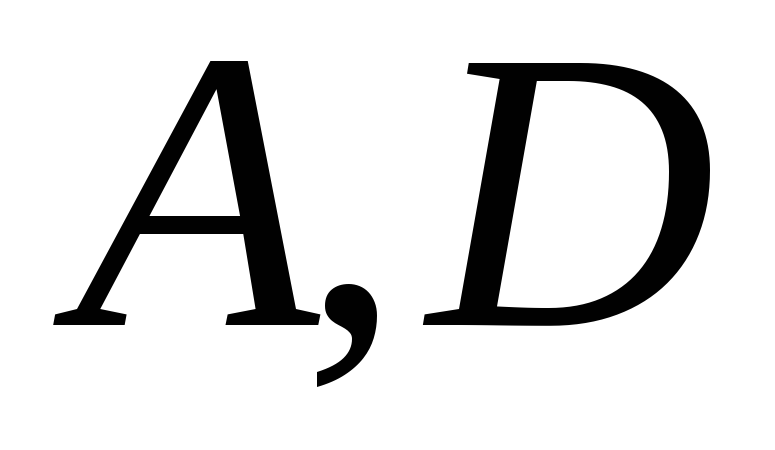 и
и
 ;
; -
обратную матрицу
 (сделать проверку).
(сделать проверку).
 ;
;
![]() ;
;
![]()
Решение.
1) Транспонируем матрицу
![]() ,
заменив строки столбцами.
,
заменив строки столбцами.
Получим
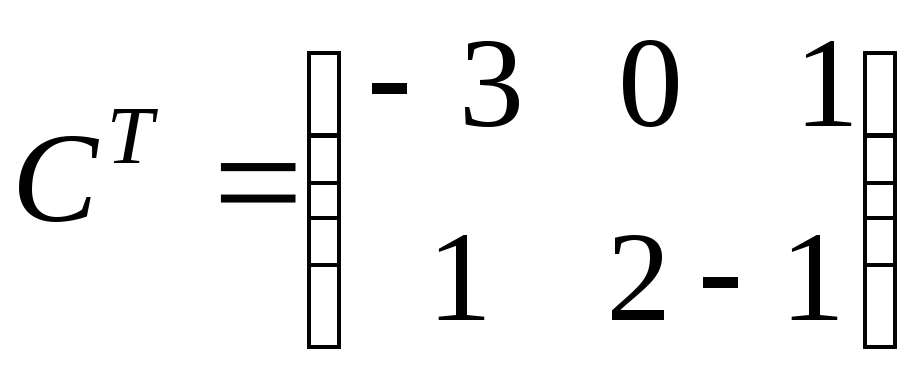 .
.
Тогда матрица![]() равна:
равна:
![]()
![]()

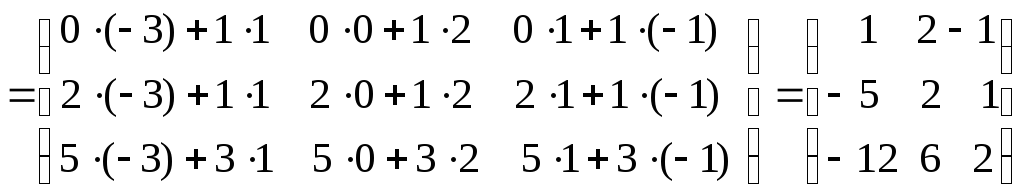 .
.
Теперь найдем матрицу
![]() :
:
![]()
 .
.
2) Будем вычислять определители матриц различными способами.
Найдем определитель матрицы
![]() ,
разложив его по элементам первой строки:
,
разложив его по элементам первой строки:
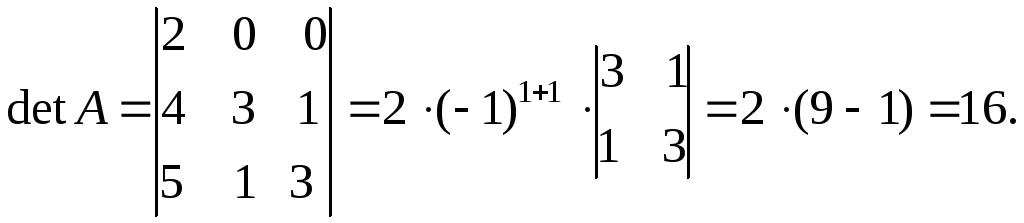
Вычислим определитель матрицы
![]() ,
используя свойства определителей
(римскими цифрами обозначены номера
строк):
,
используя свойства определителей
(римскими цифрами обозначены номера
строк):
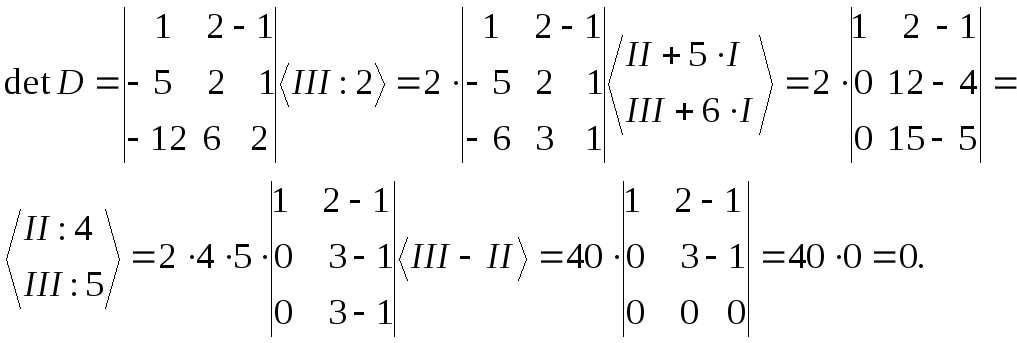 Вычислим определитель матрицы
Вычислим определитель матрицы
![]() по правилу треугольников:
по правилу треугольников:
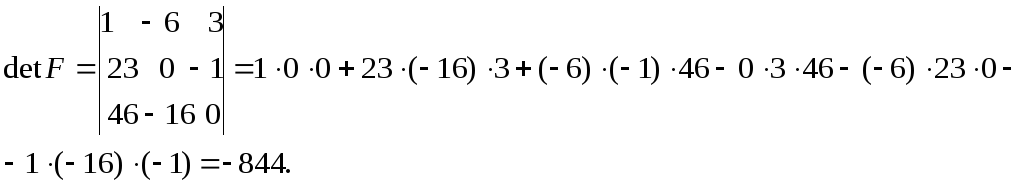
3) Матрица
![]() –
неособенная (
–
неособенная (![]() ),
следовательно, она имеет обратную.
Найдем алгебраические дополнения
элементов матрицы
),
следовательно, она имеет обратную.
Найдем алгебраические дополнения
элементов матрицы
![]() :
:

Составим из алгебраических дополнений
присоединенную матрицу и разделим ее
элементы на определитель матрицы
![]() .
.
Тогда обратная матрица
![]() окажется равной:
окажется равной:

Сделаем проверку:

Проверить самостоятельно, что
![]()
Ответ: 1)
![]()
 ;
;
![]()
 ;
2)
;
2)![]()
3)

Задание №2.
![]()
Решить систему линейных уравнений

1) методом Крамера; 2) матричным методом; 3) методом Гаусса.
Решение.
1) Выпишем матрицу системы и найдем ее определитель (например, по правилу треугольников):
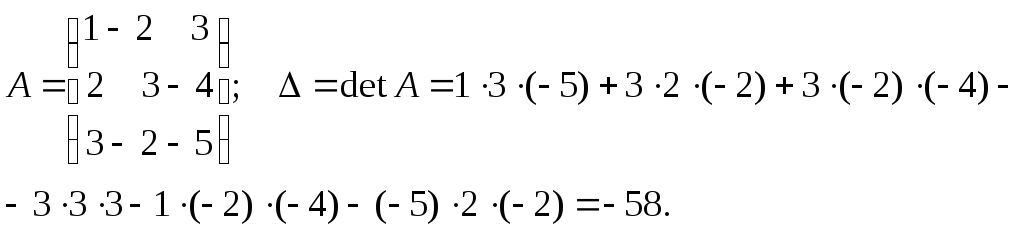
Теперь найдем вспомогательные определители
![]() ,
заменяя в исходной матрице
,
заменяя в исходной матрице
![]()
![]()
![]() -ый
столбец на столбец свободных членов
(
-ый
столбец на столбец свободных членов
(![]() =
1,2,3).
=
1,2,3).
Получим:

Применяя формулы Крамера, найдем решение системы:
 т.е.
т.е.
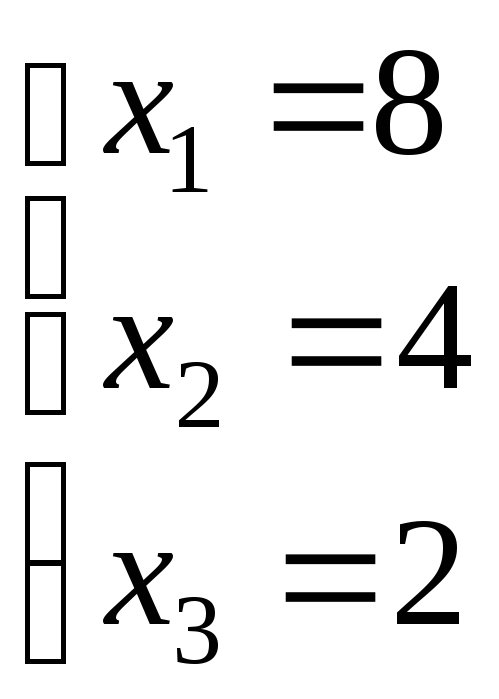 .
.
Сделаем проверку (самостоятельно!) и убедимся, что найденные значения неизвестных действительно являются решением исходной системы.
2) Матричный метод решения системы основывается на формуле:
![]() ,
где
,
где
 –
столбец неизвестных,
–
столбец неизвестных,
![]() –
обратная матрица системы,
–
обратная матрица системы,
![]() –
столбец свободных членов.
–
столбец свободных членов.
Матрица
![]() –
неособенная (
–
неособенная (![]() ),
следовательно, она имеет обратную.
Найдем
),
следовательно, она имеет обратную.
Найдем
![]() (см.
задание 1).
(см.
задание 1).
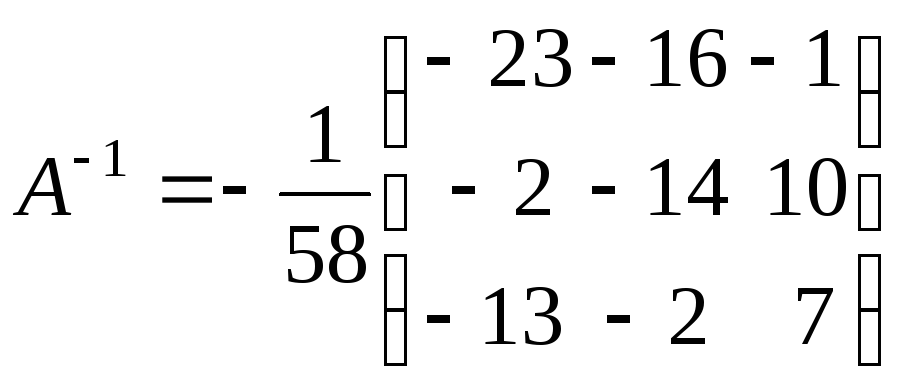 .
.
Проверьте самостоятельно, что обратная матрица найдена верно!
Тогда
![]()
 .
Следовательно,
.
Следовательно,
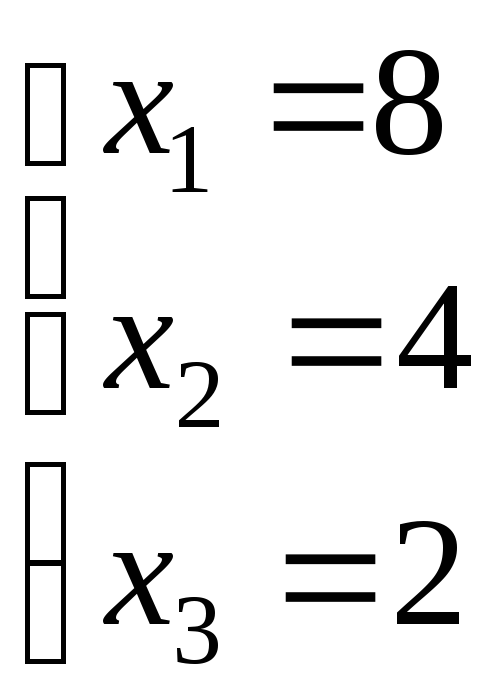 .
.
3) Метод Гаусса состоит в последовательном исключении неизвестных.
Составим расширенную матрицу, приписав справа к матрице системы столбец свободных членов. Преобразуем полученную матрицу с помощью элементарных преобразований и приведем её к трапециевидной форме («прямой ход Гаусса»). Заметим, что при решении систем, преобразуют только строки матрицы!
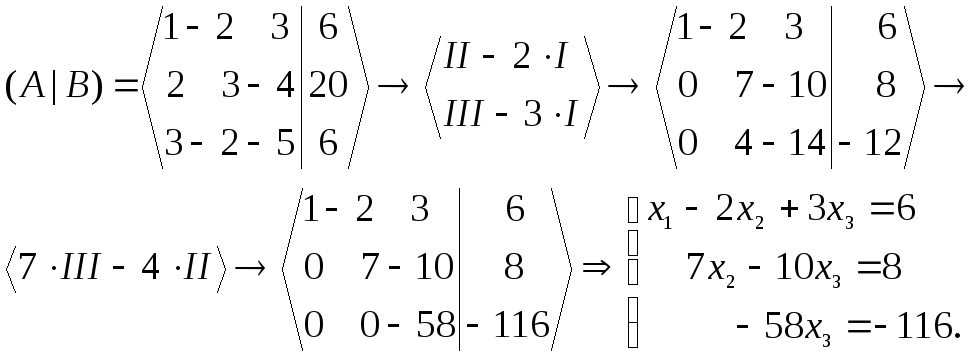
Полученная система равносильна исходной. Прочитав её снизу вверх («обратный ход Гаусса»), получим:
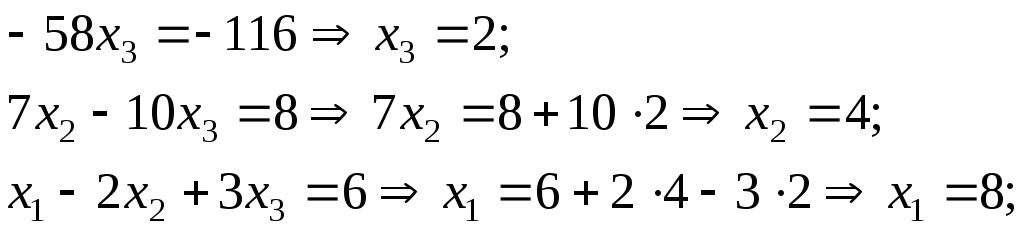

Ответ:
 .
.
Задание №3.
Найти ранг матрицы
 .
.
Решение.
Приведем данную матрицу с помощью элементарных преобразований к трапециевидной форме. Заметим, что, вычисляя ранг матрицы, можно преобразовывать как строки, так и столбцы!


Из второго, третьего и четвертого
столбца полученной матрицы можно
составить определитель (минор), отличный
от нуля (он выделен пунктиром). Это
наибольший по размеру ненулевой минор
(базисный минор), следовательно, его
размерность и равна рангу матрицы, т.е.
![]() Ответ:
Ответ:
![]()
Задание №4.
Исследовать систему с помощью теоремы Кронекера–Капелли и найти (в случае совместности) ее решения.
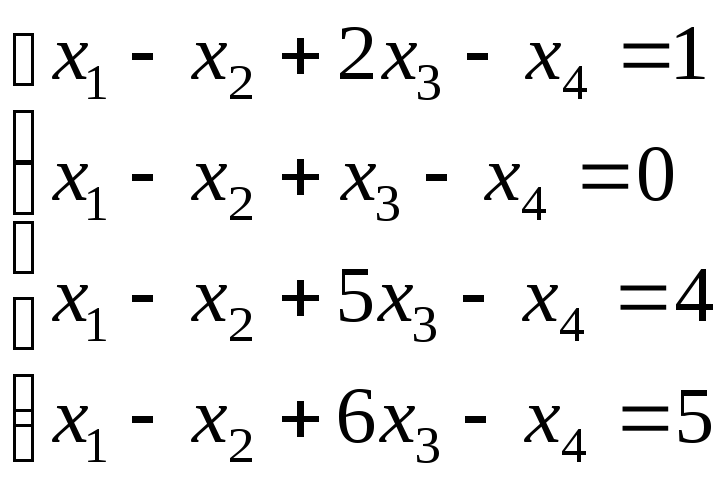
Решение.
Выпишем расширенную матрицу системы и преобразуем её с помощью элементарных преобразований к трапециевидной форме.



Наибольший порядок ненулевого минора,
как матрицы системы, так и расширенной
матрицы системы равен 2:
![]() Следовательно, согласно теореме
Кронекера-Капелли, система совместна,
т.е. имеет решения. Поскольку число
неизвестных (
Следовательно, согласно теореме
Кронекера-Капелли, система совместна,
т.е. имеет решения. Поскольку число
неизвестных (![]() )
больше ранга матрицы, то система является
неопределенной, т.е. имеет бесконечное
множество решений.
)
больше ранга матрицы, то система является
неопределенной, т.е. имеет бесконечное
множество решений.
Найдем общее решение системы. Базисные
неизвестные – это
![]() ,
коэффициенты при которых входят в
ненулевой (базисный) минор. Остальные
неизвестные – параметрические или
свободные. Решим систему относительно
базисных неизвестных (читаем снизу
вверх).
,
коэффициенты при которых входят в
ненулевой (базисный) минор. Остальные
неизвестные – параметрические или
свободные. Решим систему относительно
базисных неизвестных (читаем снизу
вверх).
![]()
Итак, придавая свободным неизвестным произвольные значения, получим бесконечно много частных решений системы.
Общее решение можно записать в виде: ,
,
где
![]() –
любые числа.
–
любые числа.
Подставив полученные выражения для неизвестных в исходную систему, убеждаемся в том, что решение найдено верно (сделать проверку самостоятельно!).
Ответ:
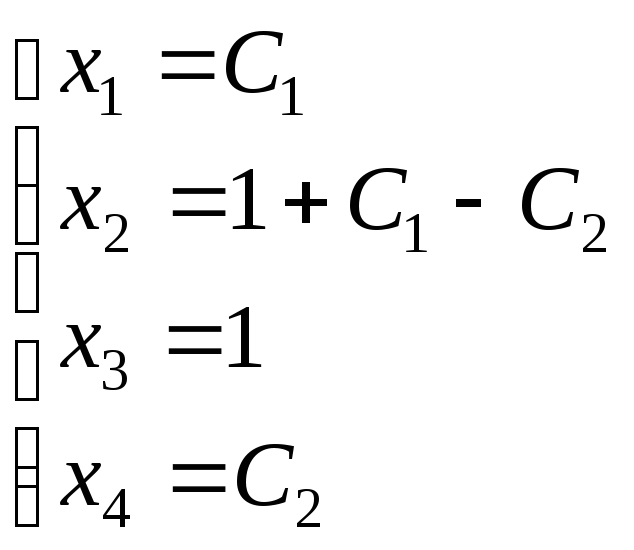 ,
где
,
где
![]() –
любые числа.
–
любые числа.
Задание №5.
Доказать, что векторы
![]() линейно зависимы и найти эту зависимость:
линейно зависимы и найти эту зависимость:
![]()
Решение.
Три вектора линейно зависимы тогда и только тогда, когда их смешанное произведение равно нулю. Имеем:

Значит, векторы линейно зависимы. Найдем эту зависимость.
Выразим один из векторов, например
![]() ,
через остальные. Другими словами, найдем
коэффициенты
,
через остальные. Другими словами, найдем
коэффициенты
![]() и
и
![]() в разложении:
в разложении:
![]()
Распишем последнее равенство по координатам, получим систему:
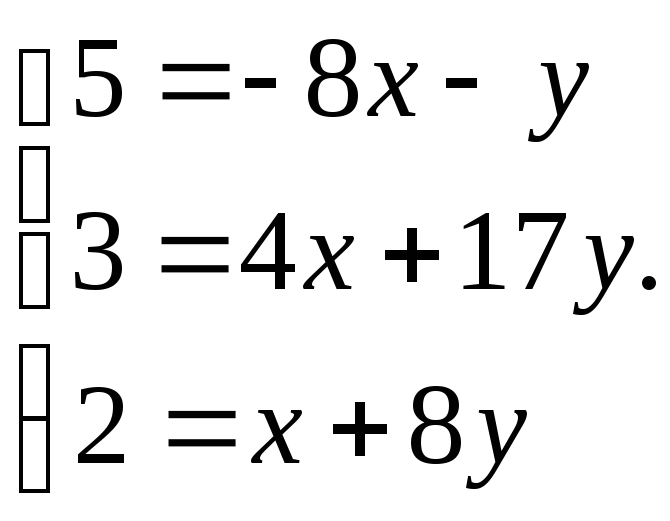
Решим систему методом Гаусса:

Итак,
![]()
Ответ:
![]()
Задание №6.
Дан
![]()
Найти:
1) длину и уравнение стороны
![]() ;
;
2) длину и уравнение медианы
![]() ;
;
3) длину и уравнение высоты
![]() ;
;
4) площадь
![]() ;
;
5) угол
![]() .
.
Решение.
1) Используем уравнение прямой на плоскости через две точки:
![]()
Подставляя координаты точек
![]() ,
получим:
,
получим:
![]()
![]() –
уравнение стороны
–
уравнение стороны
![]() .
.
Длина стороны
![]() равна длине вектора
равна длине вектора
![]() .
.
![]() ед.
ед.
2) Точка
![]() –
середина отрезка
–
середина отрезка
![]()
 .
.
Итак,
![]() Уравнение медианы
Уравнение медианы
![]() будет
иметь вид:
будет
иметь вид:
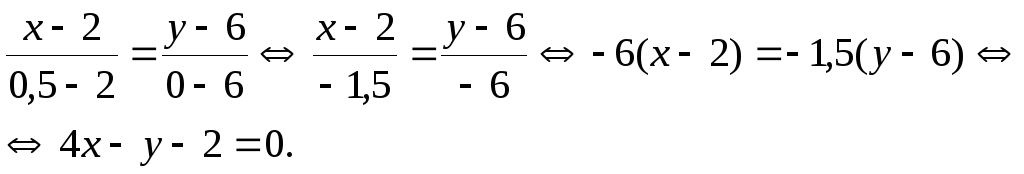
Длина медианы
![]() равна длине вектора
равна длине вектора
![]()
![]() ед.
ед.
3) Для высоты
![]() используем уравнение прямой на плоскости
через точку и нормаль:
используем уравнение прямой на плоскости
через точку и нормаль:
![]() ,
где нормаль
,
где нормаль
![]() –
вектор перпендикулярный прямой, а точка
–
вектор перпендикулярный прямой, а точка
![]() принадлежит данной прямой.
принадлежит данной прямой.
Имеем
![]()
![]() – уравнение высоты
– уравнение высоты
![]() .
.
Длина высоты
![]() –
расстояние от точки
–
расстояние от точки
![]() до прямой
до прямой
![]() .
Уравнение прямой
.
Уравнение прямой
![]() имеет
вид:
имеет
вид:
![]()
Используем формулу расстояния от точки
![]() до прямой
до прямой
![]() :
:
![]()
Получим:
![]() ед.
ед.
4) Площадь
![]() можно найти по формуле:
можно найти по формуле:
 ,
где
,
где
![]() –
координаты вершин треугольника.
–
координаты вершин треугольника.
Имеем:
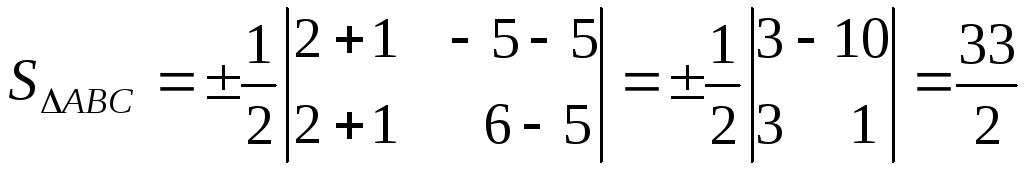 кв. ед.
кв. ед.
Замечание. Вычисленное значение площади
можно проверить по формуле:
![]() (верно!).
(верно!).
5) Угол
![]() находим как угол между векторами
находим как угол между векторами
![]() и
и
![]() .
.

Ответ: 1) Сторона
![]() ед.;
ед.;
2) медиана![]() ед.;
ед.;
3) высота
![]() ед.;
ед.;
4)
![]() кв. ед.; 5)
кв. ед.; 5)![]()
Задание №7.
Дана пирамида
![]()
Найти:
1) длину и уравнение ребра
![]() ;
;
2) площадь и уравнение грани
![]() ;
;
3) объем пирамиды;
4) длину и уравнение высоты, опущенной
из вершины
![]() на плоскость
на плоскость
![]() ;
;
5) угол между ребром
![]() и гранью
и гранью
![]() .
.
6) угол между гранями
![]() и
и
![]()
Решение.
1) Используем уравнение прямой в пространстве через две точки:
![]()
Подставляя координаты точек
![]() ,
получим:
,
получим:
![]() – уравнение ребра
– уравнение ребра
![]() .
.
Длина стороны
![]() равна длине вектора
равна длине вектора
![]() .
.
![]() ед.
ед.
2) Площадь грани
![]() равна площади
равна площади
![]() ,
которую можно найти через векторное
произведение по формуле:
,
которую можно найти через векторное
произведение по формуле:
![]()

![]() кв. ед.
кв. ед.
Уравнение грани – это уравнение плоскости через три точки:

Подставляя в это уравнение координаты
точек
![]() ,
получим уравнение грани
,
получим уравнение грани
![]() :
:

3) Объем пирамиды
![]() равен
равен
![]() модуля смешанного произведения векторов
модуля смешанного произведения векторов
![]() .
Найдем координаты векторов:
.
Найдем координаты векторов:
![]()
Тогда смешанное произведение равно:

![]() куб. ед.
куб. ед.
4) Из уравнения грани
![]() :
:
![]() найдем координаты вектора нормали
найдем координаты вектора нормали
![]() ,
расположенного перпендикулярно плоскости
,
расположенного перпендикулярно плоскости
![]() ,
а значит параллельно высоте, опущенной
из вершины
,
а значит параллельно высоте, опущенной
из вершины
![]() .
.
Используем каноническое уравнение прямой в пространстве:
![]()
Подставляя вместо
![]() координаты точки
координаты точки
![]() ,
а вместо
,
а вместо
![]() координаты вектора нормали
координаты вектора нормали
![]() ,
получим уравнение высоты:
,
получим уравнение высоты:
![]()
Длина высоты
![]() –
расстояние от точки
–
расстояние от точки
![]() до плоскости
до плоскости
![]() .
Используем формулу
.
Используем формулу
![]()
Получим:
![]() ед.
ед.
5) Угол
![]() между ребром
между ребром
![]() и гранью
и гранью
![]() найдем как угол между векторами
найдем как угол между векторами
![]() .
.
Имеем:
![]()
![]()
Заметим, что угол
![]() по определению всегда острый.
Поэтому, если
по определению всегда острый.
Поэтому, если
![]() окажется меньше нуля, то его значение
надо взять по модулю!
окажется меньше нуля, то его значение
надо взять по модулю!
6) Угол
![]() между гранями
между гранями
![]() и
и
![]() найдем как угол между нормалями к
этим граням. Плоскость
найдем как угол между нормалями к
этим граням. Плоскость
![]() имеет уравнение
имеет уравнение
![]() и, следовательно, её нормаль
и, следовательно, её нормаль
![]() .
Напишем уравнение плоскости
.
Напишем уравнение плоскости
![]() :
:

Тогда её нормаль
![]() .
Находим косинус угла между векторами
.
Находим косинус угла между векторами
![]() и
и
![]() :
:

Замечание. Угол
![]() по определению всегда острый.
Поэтому, если косинус окажется меньше
нуля, то его значение надо взять по
модулю!
по определению всегда острый.
Поэтому, если косинус окажется меньше
нуля, то его значение надо взять по
модулю!
Ответ: 1)
![]() ед.;
ед.;
2)
![]() :
:
![]() ;
;
![]() кв.
ед.;
кв.
ед.;
3)
![]() куб.
ед.;
куб.
ед.;
4)
![]() –
уравнение высоты; длина высоты
–
уравнение высоты; длина высоты![]() ед.;
ед.;
5)![]() 6)
6)![]()
Задание №8.
Определить, какая линия на плоскости задается уравнением. Сделать чертеж.
1)
![]() ;
2)
;
2)
![]() ;
;
3)
 .
.
Решение.
1) Преобразуем данное уравнение, выделив полные квадраты:
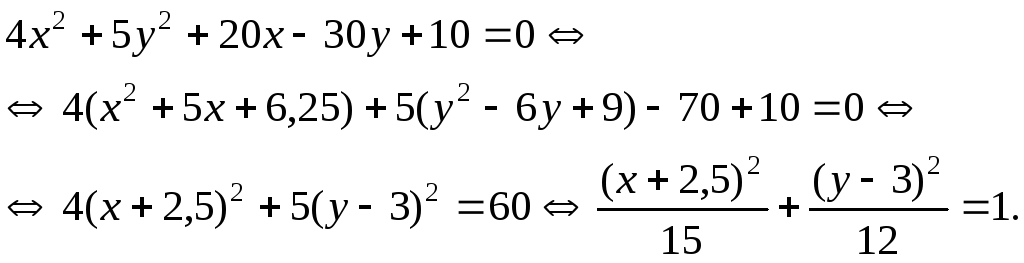
Получим уравнение эллипса с центром
в точке с координатами
![]() и полуосями
и полуосями
![]() (рис.1).
(рис.1).


2) Данное уравнение
![]() задает в полярной системе координат
кривую – кардиоиду.
задает в полярной системе координат
кривую – кардиоиду.
Меняя
![]() от
от
![]() до
до
![]() ,
вычислим значения полярного радиуса
,
вычислим значения полярного радиуса
![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
