
Справочный материал
Комплексные числа
Алгебраической формой комплексного
числа ![]() называется выражение вида
называется выражение вида![]() ,
где
,
где![]() и
и![]() – действительные числа, а
– действительные числа, а![]() – так называемая мнимая единица (
– так называемая мнимая единица (![]() ).
).
Число
![]() называется действительной частью
комплексного числа
называется действительной частью
комплексного числа![]() (
(![]() ),
число
),
число![]() -
мнимой частью
-
мнимой частью![]() (
(![]() ).
).
Два комплексных числа
![]() и
и![]() ,
отличающиеся лишь знаком мнимой части,
называютсясопряженными.
,
отличающиеся лишь знаком мнимой части,
называютсясопряженными.
Пусть даны два комплексных числа
![]() и
и![]() ,
тогда они равны, если равны их
действительные и мнимые части, т.е.
,
тогда они равны, если равны их
действительные и мнимые части, т.е. .
.
Действия над комплексными числами в алгебраической форме задаются формулами
1.

2.
![]()
В частности
![]() ;
;
3.
 .
.
К омплексное
число
омплексное
число![]() можно изобразить на плоскости
можно изобразить на плоскости![]() в виде точки
в виде точки![]() или радиус-вектора
или радиус-вектора![]() .
.
Д лина
вектора
лина
вектора![]() называетсямодулемкомплексного
называетсямодулемкомплексного![]()
ч

 исла
и обозначается
исла
и обозначается![]() или
или![]() ,
а угол
,
а угол![]() между векторомуМ
между векторомуМ
![]()

 и положительным направлением оси
и положительным направлением оси![]() называется
называется![]()
аргументомэтого комплексного числа.О х х
Главным называется значение аргумента![]() .
.
Очевидно, что![]()
![]() (1)
(1)
Полученная запись комплексного числа называется тригонометрической формой.
Модуль и аргумент комплексного числа определяются по формулам

Используя формулу Эйлера
![]()
комплексное число
![]() можно записать впоказательной форме
можно записать впоказательной форме![]() .
.
Действия над комплексными числами в тригонометрической форме выполняются по формулам:
1.
![]()
2. 
3.
![]() (2)
(2)
4.

В частности
![]() .
.
Пределы
Для нахождения пределовфункции используются следующие теоремы.
Если существуют пределы![]() и
и![]() ,
то
,
то
1.
![]() ;
;
2.
![]() ;
;
В частности,
![]() ,
где
,
где![]() ;
;
3.
 .
.
Аналогичные теоремы справедливы для пределов последовательностей.
Имеют место два замечательных предела:
1. ; 2..
Следствия:
1.![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]()
5.
![]() ;
6.
;
6.![]() ;
7.
;
7.![]() .
.
Для раскрытия неопределённостей вида
![]() и
и![]() используютправило Лопитал:
Пусть функции
используютправило Лопитал:
Пусть функции![]() и
и![]() непрерывны и дифференцируемы в окрестности
точки
непрерывны и дифференцируемы в окрестности
точки![]() и
и![]() .
Если существует предел
.
Если существует предел![]() ,
то
,
то![]() (3)
(3)
Непрерывность функции в точке
Функция
![]() называетсянепрерывнойв точке
называетсянепрерывнойв точке![]() ,
если
,
если
![]() .
(4)
.
(4)
Указанное равенство предполагает, что функция определена в точке
![]() и её окрестности и имеет предел при
и её окрестности и имеет предел при![]() .
.
Равенство (4) эквивалентно равенству
![]() ,
(5)
,
(5)
где
![]() -
лево и правосторонние пределы функции
в точке
-
лево и правосторонние пределы функции
в точке![]() .
.
Известно, что элементарные функции непрерывны в каждой точке, в которой они определены.
Точки, в которых нарушается условие непрерывности, называются точками разрывафункции. Все точки разрыва разделяются на точки разрыва первого и второго рода.
Точка разрыва
![]() называется точкойразрыва первого
родафункции
называется точкойразрыва первого
родафункции![]() ,
если в этой точке существуют конечные
пределы слева и справа
,
если в этой точке существуют конечные
пределы слева и справа![]() и
и![]() .
При этом, если
.
При этом, если![]() ,
то точка
,
то точка![]() называется точкойустранимого разрыва;
а если
называется точкойустранимого разрыва;
а если![]() ,
то точкойконечного разрыва.
,
то точкойконечного разрыва.
Точка разрыва
![]() называется точкойразрыва второго
родафункции
называется точкойразрыва второго
родафункции![]() ,
если хотя бы один из односторонних
пределов в этой точке не существует или
равен бесконечности.
,
если хотя бы один из односторонних
пределов в этой точке не существует или
равен бесконечности.
Производная
Правила дифференцирования
Пусть
![]() ,
тогда
,
тогда
 ;
; ;
в частности:
;
в частности: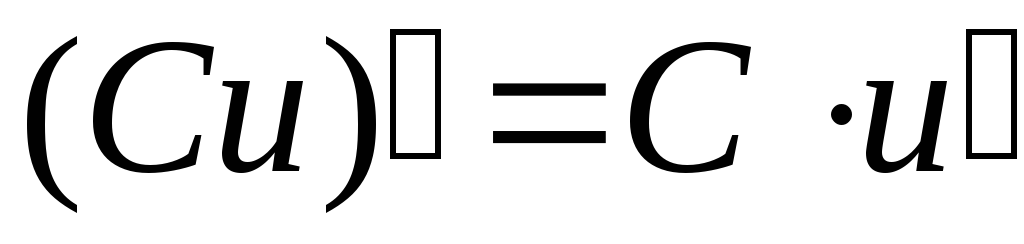 ,
, ;
; ;
;если
 ,
где
,
где ,
тогда
,
тогда
 .
.
Таблица производных
 ;
; ;
; ;
в частности:
;
в частности: ;
; ;
в частности:
;
в частности: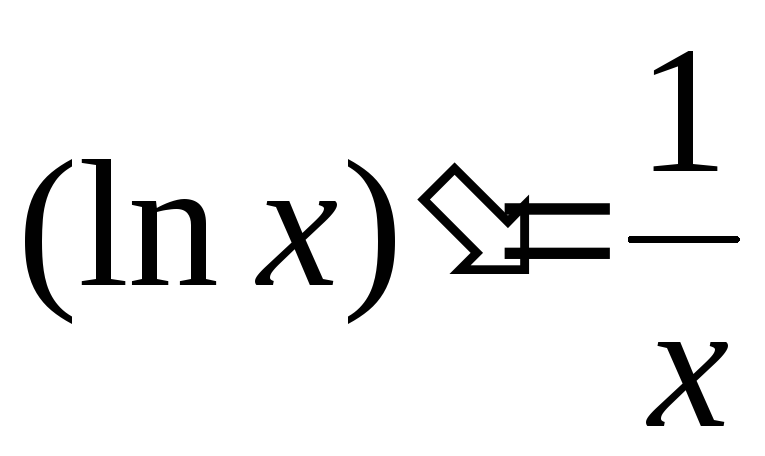 ;
; ;
6.
;
6. ;
;
7.
![]() ;
8.
;
8.![]() ;
;
 ;
;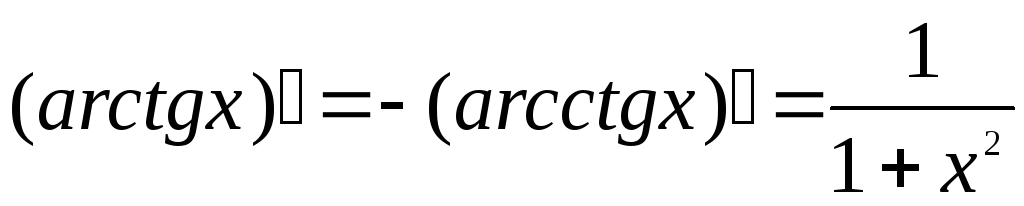 .
.
5. Исследование функции и построение её графика Основные свойства функций
1.Функция
![]() называетсявозрастающей (убывающей)на множестве
называетсявозрастающей (убывающей)на множестве![]() ,
если для любых
,
если для любых![]()
![]() .
.
2. Функция
![]() называетсяпериодической, если
существует число
называетсяпериодической, если
существует число![]() такое, что
такое, что![]() .
Число
.
Число![]() называетсяпериодомфункции.
называетсяпериодомфункции.
3. Функция
![]() называетсячетной, если
называетсячетной, если![]() .
График четной функциисимметричен
относительно оси
.
График четной функциисимметричен
относительно оси
![]() .Функция
.Функция![]() называетсянечетной, если
называетсянечетной, если![]() .
График нечетной функциисимметричен
относительно начала координат.
.
График нечетной функциисимметричен
относительно начала координат.
Четная и нечетная функция должна иметь область определения симметричную относительно начала координат.
Исследование функции с помощью производной
1.Монотонность – возрастание или убывание функции.
Если функция
![]() дифференцируема на интервале
дифференцируема на интервале![]() и
и![]() (
(![]() )
для всех
)
для всех![]() ,
то эта функция возрастает (убывает)
на интервале
,
то эта функция возрастает (убывает)
на интервале
![]() .
.
2.Экстремумы – максимумы и минимумы функции.
Если непрерывная функция
![]() дифференцируема в некоторой окрестности
точки
дифференцируема в некоторой окрестности
точки![]() и
и![]() или не существует, а при переходе через
точку
или не существует, а при переходе через
точку![]() производная меняет знак с «–» на «+»,
то
производная меняет знак с «–» на «+»,
то![]() – точка минимума, а при смене знака с
«+» на «–»
– точка минимума, а при смене знака с
«+» на «–»![]() –
точка максимума.
–
точка максимума.




 знак
знак![]() –
–![]() + знак
+ знак![]() +
+![]() –
–
поведение![]() minповедение
minповедение![]() max
max
