Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Книги от Прохорова / ВЫЧИСЛИТЕЛЬНЫЙ ПРАКТИКУМ по Mathcad

.pdf

Скачиваний:

Добавлен:

16.03.2015

Размер:

792.28 Кб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

ВЫЧИСЛИТЕЛЬНЫЙ ПРАКТИКУМ

ПО ОРТОГОНАЛЬНЫМ МОДЕЛЯМ

2009 год

Приложение 2

ВЫЧИСЛИТЕЛЬНЫЙ ПРАКТИКУМ 1. «ИССЛЕДОВАНИЕ СВОЙСТВ ОРТОГОНАЛЬНЫХ ПОЛИНОМОВ»

Цель работы: изучение основных свойств классических ортогональных полиномов, приобретение навыков работы с ними.

1. Представление ортогональных полиномов k - ого порядка

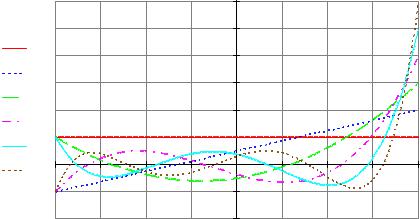
1.1. Представить ортогональные полиномы в форме Родрига и получить аналитические выражения и графики для первых шести порядков.

P1(k ,x) :=

1 if

(−1)k

k+1

− x)

(1 + x)

otherwise

k! 2k (1 − x)

P1(0,x) simplify

→ 1

P1(1,x) simplify

→

3 x

P1(2,x) simplify

→

5 x2

+ x −

P1(3,x) simplify

→

35 x3

15 x2

−

15 x

−

P1(4,x) simplify

→

63 x4

7 x3

−

21 x2

−

3 x

P1(5,x) simplify

→

231 x5

105 x4

− 105 x3

−

35 x2

35 x

159

				6
P1(0,x)				5
P1(0,x)
P1(1,x)				4
P1(1,x)
P1(2,x)				3
P1(3,x)				2
P1(4,x)				1
				1
P1(5,x)
− 1	− 0.75	− 0.5	− 0.25	0	0.25	0.5	0.75	1
				− 1
				− 2
				x

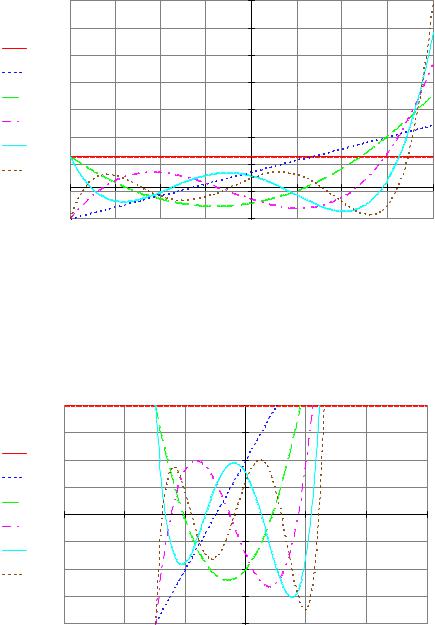
1.2. Представить ортогональные полиномы в виде конечного ряда и получить аналитические выражения и графики для первых шести порядков.

(k + s + 1)! x − 1 s

P(k ,x) := ∑

s! (k − s)! k! (s + 1)!

s = 0

P(0,x) simplify

→ 1

P(1,x) simplify

→

3 x

P(2,x) simplify

→

5 x2

+ x −

P(3,x) simplify

→

35 x3

15 x2

−

15 x

−

P(4,x) simplify

→

63 x4

7 x3

−

21 x2

−

3 x

P(5,x) simplify

→

231 x5

105 x4

− 105 x3

−

35 x2

35 x

160

			6
P(0,x)			5.125
P(0,x)
P(1,x)			4.25
P(1,x)
P(2,x)			3.375
P(3,x)			2.5
P(4,x)			1.625
			1.625
P(5,x)			0.75
			0.75
− 1	− 0.75	− 0.5	− 0.125	0	0.25	0.5	0.75	1
− 1	− 0.75	− 0.5	− 0.25	0	0.25	0.5	0.75	1
			− 1
				x

2. Определить интервал ортогональности [a, b]. Рассчитать ортогональные полиномы k - ого порядка на концах интервала ортогональности.

				1
P(0,x)				0.75
P(0,x)
P(1,x)				0.5
P(1,x)
P(2,x)				0.25
P(3,x)	− 2	− 1.333	− 0.667	0	0.667	1.333	2
P(4,x)	− 2	− 1.333	− 0.667	0	0.667	1.333	2
P(4,x)				− 0.25
				− 0.25
P(5,x)				− 0.5
				− 0.5
				− 0.75
				− 1
				x

161

a := −1 k := 0.. 5

b := 1	P(k ,−1)	P(k ,1) =

	1	1
	-1	2

	1	3

	-1	4

	1	5

	-1	6

3. Определение нормы ортогональных полиномов.

3.1. Определить значения нормы ортогональных полиномов из выражения (1. 7).

Результат - в виде матрицы значений с разрядностью (k, m), привести графическую интерпретацию.

k := 6

μ(x) := 1 − x

i := 0.. k − 1

m := k

j := 0.. m − 1

⌠b

NormP(i,j ) := P(i,x) P(j ,x) μ(x) dx

⌡a

NormMP := matrix(k ,m,NormP)

	2		0	0	0	−0	0
		0	1	0	0	0	−0
		0	0	0.667	0	0	0
NormMP =		0	0	0.667	0	0	0
NormMP =		0	0	0	0.5	0	−0


		−0	0	0	0	0.4	−0
	0		−0	0	−0	−0	0.333

162

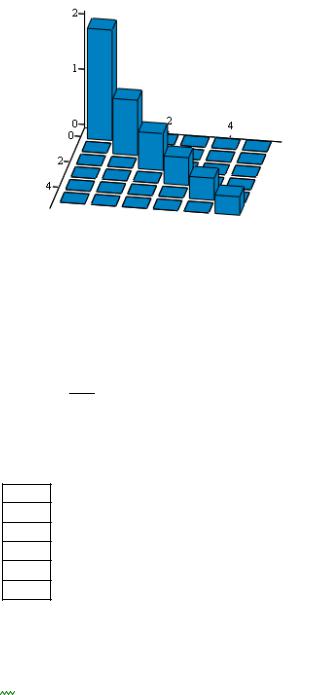
NormMP

3.2. Определить значение нормы ортогональных полиномов k - ого порядка, используя выражение, приведенное в таблице 1.2. Результат представить в виде вектора значений.

2 NormPTi := i + 1

NormPTi =

0.667

0.5

0.4

0.333

4. Проверить выполняемость 1 - ого условия ортогональности.

m := 0.. 15

⌠b

Norm(m,n) := P(m,x) P(n ,x) μ(x) dx

⌡a

163

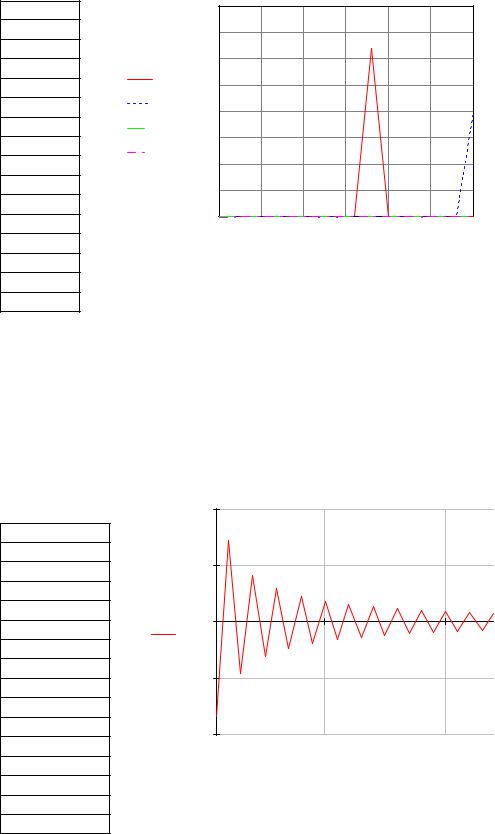
Norm(m,16) =

1.768·10-6

-1.285·10-6

6.731·10-7

5.008·10-8

3.222·10-7

-1.308·10-7

-4.025·10-7

7.898·10-7

-9.839·10-7

9.833·10-7

-8.235·10-7

5.652·10-7

-2.808·10-7

3.314·10-8

-1.771·10-7

2.112·10-7

0.25
0.219
Norm(m,9) 0.188
Norm(m,15)0.156
Norm(m,16)0.125
Norm(m,19)0.094
0.063
0.031
0	0	2.5	5	7.5	10	12.5	15
				m
1 - ое условие ортогональности выполнено

5. Проверить выполняемость 2 - ого условия ортогональности.

x := 0	j := 1..25
f (j ,x) := P(j ,x)
solution j	:= root (f (j ,x) ,x)

solution j =

-0.333

0.29

-0.181

0.167

-0.124

0.117

-0.094

0.09

-0.076

0.073

-0.064

0.062

-0.055

0.053

-0.048

...

0.4
0.2
solutionj	10	20
	10	20
− 0.2
− 0.4
		j
2 - ое условие ортогональности выполнено

164

Приложение 5

ВЫЧИСЛИТЕЛЬНЫЙ ПРАКТИКУМ 2. «ИССЛЕДОВАНИЕ СВОЙСТВ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ»

Цель работы: исследование свойств ортогональных функций и определение их основных характеристик.

1. Получение ортогональных функций k-ого порядка:

1.1. Получить ортогональные функции из ортогональных полиномов k-ого порядка путем введения соответствующей замены. Найти аналитические выражения и графики для первых шести порядков:

(k + s + 1)! x − 1 s

P1(k ,x) := ∑

k! (s + 1)!

μ(x) := 1

− x

(k − s)! s!

s = 0

x(τ ,γ ) := 1 − 2e− γ τ

x(τ ,γ ) → 2 γ e− γ τ

μ(τ ,γ ) := 1 − x(τ ,γ )

dτ

(k + s + 1)! x(τ ,γ ) − 1 s

x(τ ,γ )

μ(τ ,γ )

dτ

P1(k ,τ ,γ ) := ∑

− s)! s! k! (s + 1)!

2γ

s = 0

γ := 1

P1(0,τ ,γ ) simplify → e− τ

P1(1,τ ,γ ) simplify → 2 e− τ − 3 e− 2 τ

P1(2,τ ,γ ) simplify → 3 e− τ − 12 e− 2 τ + 10 e− 3 τ

P1(3,τ ,γ ) simplify → 4 e− τ − 30 e− 2 τ + 60 e− 3 τ − 35 e− 4 τ

171

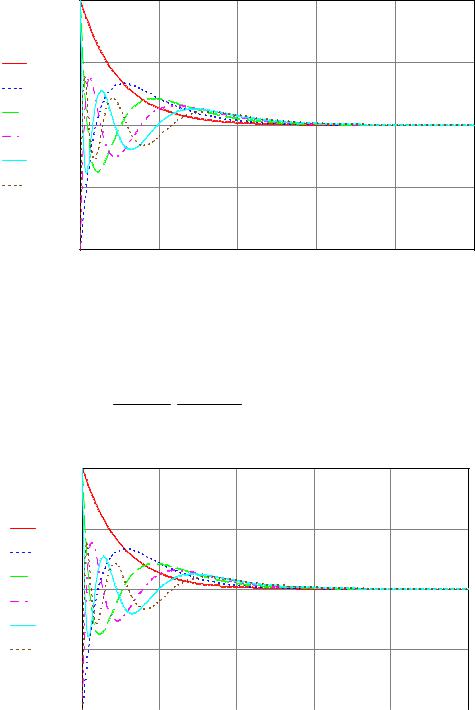
P1(4,τ ,γ ) simplify		→ 5 e− τ		− 60 e− 2 τ + 210 e− 3 τ					− 280 e− 4 τ + 126 e− 5 τ
P1(5,τ ,γ ) simplify		→ 6 e− τ		− 105 e− 2 τ + 560 e− 3 τ					− 1260 e− 4 τ + 1260 e− 5 τ		− 462 e− 6 τ
	1
P1(0,τ ,γ )	0.5
P1(1,τ ,γ )	0.5
P1(1,τ ,γ )
P1(2,τ ,γ )
P1(3,τ ,γ ) 0
P1(4,τ ,γ )
P1(5,τ ,γ )
− 0.5
	− 10			2	4				6	8	10
							τ
1.2. Получить ортогональные функции, используя представление, приведенное в
таблице. Найти аналитические выражения и графики										для первых шести порядков:
	k		k!		(k + s + 1)!	s		− (s+1) γ τ
P(k ,τ ,γ ) := ∑		(k − s)! s!			k! (s + 1)! (−1)		e
	s = 0
	1
P(0,τ ,γ )	0.5
P(1,τ ,γ )	0.5
P(2,τ ,γ )
P(3,τ ,γ )	0
P(4,τ ,γ )
P(5,τ ,γ )
− 0.5

− 1
− 1	0	2	4	6	8	10
				τ

172

2. Рассчитать значения ортогональных функций k-ого порядка в "нуле".

k := 0..5

P(k ,0,γ )

-1

3. Определение нормы ортогональных функций:

3.1. Определить значение нормы ортогональных функций из выражения (2.3) (см. содержание лабораторной работы). Результат представить в виде матрицы значений с разрядностью (k,m), Привести графическую интерпретацию.

k := 6

i := 0..k − 1

m := k

μ(τ ,γ ) := 1

j := 0..m − 1

⌠∞

NormP(i,j ) := P(i,τ ,γ ) P(j ,τ ,γ ) μ(τ ,γ ) dτ

⌡0

NormMP := matrix(k ,m,NormP)

	0.5		−0	−0	−0	−0	−0
		−0	0.25	−0	−0	−0	−0
		−0	−0	0.167	−0	−0	−0
NormMP =		−0	−0	0.167	−0	−0	−0
NormMP =		−0	−0	−0	0.125	−0	−0


		−0	−0	−0	−0	0.1	−0
	−0		−0	−0	−0	−0	0.083

173

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в папке Книги от Прохорова

#
16.03.2015787.99 Кб82Автоматизация комплексного управления безопасностью предприятия.pdf
#
16.03.20156.62 Mб55АВТОМАТИЗИРОВАННАЯ СИСТЕМА КСА СП.pdf
#
16.03.20151.11 Mб47Автоматизированные системы.pdf
#
16.03.201511.46 Mб59АППРОКСИМАТИВНЫЙ АНАЛИЗ СЛУЧАЙНЫХ ПРОЦЕССОВ изд.2.pdf
#
16.03.20155.92 Mб59АППРОКСИМАТИВНЫЙ АНАЛИЗ СЛУЧАЙНЫХ ПРОЦЕССОВ.pdf
#
16.03.2015792.28 Кб72ВЫЧИСЛИТЕЛЬНЫЙ ПРАКТИКУМ по Mathcad.pdf
#
16.03.20154.01 Mб61МАТОПИСАНИЕ И МОДЕЛИРОВАНИЕ СП.pdf
#
16.03.20151.36 Mб52Методы и средства проектирования профилей ИСОКБП.pdf
#
16.03.20158.39 Mб56МОДЕЛИРОВАНИЕ И АНАЛИЗ СП. ЛАБОРАТОРНЫЙ ПРАКТИКУМ изд.2.pdf
#
16.03.20153.41 Mб51МОДЕЛИРОВАНИЕ И АНАЛИЗ СП. ЛАБОРАТОРНЫЙ ПРАКТИКУМ.pdf
#
16.03.201540.96 Кб44Название книг.doc