Основные формулы

1. Функция распределения Ферми-Дирака для электронов (f_n) и дырок (f_p):

, ,

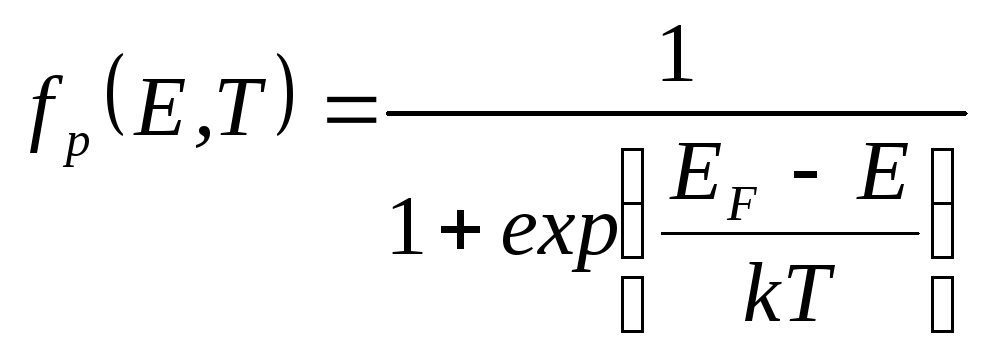где E – энергия, отсчитываемая от произвольно выбранного уровня (обычно от уровня E_c), эВ; E_F – энергия Ферми, отсчитанная от того же уровня, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град.

2. Функция распределения Максвелла-Больцмана для электронов (f_n) и дырок (f_p):

, .

где E – энергия, отсчитываемая от произвольно выбранного уровня (обычно от уровня E_c), эВ; E_F – энергия Ферми, отсчитанная от того же уровня, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град.

3. Концентрация свободных электронов (n) и дырок (p) в полупроводнике, см^-3:

, .

где N_C, N_V – эквивалентные плотности состояний электронов и дырок, м^-3; E_F – энергетический уровень Ферми, эВ; E_C – энергетический уровень зоны проводимости, эВ; E_V – энергетический уровень валентной зоны, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град.

4. Эквивалентные плотности состояний электронов (N_C) и дырок (N_V), см^-3:

, .

где m_n, m_p – эффективные массы электрона и дырки в полупроводнике, кг; m – масса свободного электрона, 9,1·10^-31 кг; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град; h – постоянная Планка, h = 6,262·10^-34 Дж·c = 4,141·10^-15 эВ·c.

5. Уровень Ферми собственного полупроводника, эВ:

,

где E_q – ширина запрещенной зоны, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град; m_n, m_p – эффективные массы электрона и дырки в полупроводнике, кг.

6. Уровень Ферми донорного полупроводника, эВ:

,

где E_c – энергетический уровень зоны проводимости, эВ; E_d – энергетический уровень донора, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град; N_d, N_c – концентрация донорной примеси и эквивалентная плотность состояний электронов в зоне проводимости, м^-3.

7. Закон действующих масс:

,

где n_n, n_p – концентрация основных и неосновных носителей заряда в полупроводнике n-типа, м^-3; n_p, p_p – концентрация неосновных и основных носителей заряда в полупроводнике p-типа, м^-3; n_i, p_i – концентрация электронов и дырок в собственном (беспримесном) полупроводнике, м^-3.

8. Концентрация носителей заряда в собственном полупроводнике, см^-3:

,

где N_C, N_V – эквивалентные плотности состояний электронов и дырок в зоне проводимости и валентной зоне, м^-3; E_q – ширина запрещенной зоны, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град.

9. Температура истощения примеси (T_s), К и ионизации матричных атомов (T_i), К:

, ,

где E_c, E_d – энергетический уровень зоны проводимости и донора, эВ; E_q – ширина запрещенной зоны, эВ; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; N_C, N_V – эквивалентные плотности состояний электронов и дырок в зоне проводимости и валентной зоне, см^-3; N_d – концентрация донорной примеси, см^-3.

10. Плотность дрейфового тока носителей заряда, А/см².

,

где e – заряд электрона, 1,6*10^-19 Кл; n, p – концентрация электронов, дырок, см^-3; μ_n, μ_p – подвижность электронов, дырок, см²/(В·с); σ_n – удельная электрическая проводимость, 1/(Ом·см); E₀ – напряженность электрического поля, В/см; , - скорость направленного движения носителей заряда, см/сек.

11. Плотность диффузионного тока носителей заряда, А/см²:

,

где e – заряд электрона, 1,6*10^-19 Кл; n, р – концентрация электронов, дырок, см^-3; D_n, D_p – коэффициенты диффузии электронов, дырок, см²/сек; х – координата, см.

12. Соотношение Эйнштейна для коэффициента диффузии, см²/сек:

, ,

где e – заряд электрона, 1,6*10^-19 Кл; μ_n, μ_p – подвижность электронов и дырок, см²/(В·с); k = 1,38·10^-23 Дж/град – постоянная Больцмана; T – абсолютная температура, град.

13. Полная удельная проводимость и подвижность носителей заряда, 1/(Ом*см):

, ,

где e – заряд электрона, 1,6*10^-19 Кл; n, p – концентрация электронов и дырок, см^-3; μ_n, μ_p – подвижность электронов и дырок, см²/(В·с); m_n, m_p – эффективные массы электрона и дырки в полупроводнике, кг; τ_п – время свободного пробега, с.

14. Удельная проводимость собственного полупроводника, 1/(Ом*см):

,

где e – заряд электрона, 1,6*10^-19 Кл; μ_n, μ_p – подвижность электронов и дырок, м²/(В·с); E_q – ширина запрещенной зоны, эВ; m_n, m_p – эффективные массы электрона и дырки в полупроводнике, кг; h – постоянная Планка, h = 6,262·10^-34 Дж·c = 4,141·10^-15 эВ·c; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; T – абсолютная температура, град.

15. Удельная проводимость примесного полупроводника, 1/(Ом*см):

,

где e – заряд электрона, 1,6*10^-19 Кл; μ_n, μ_p – подвижность электронов и дырок, см²/(В·с); N_Д, N_A – концентрация донора и акцептора, см^-3; n_n, p_n – концентрация электронов и дырок в полупроводнике n-типа, см^-3; p_p, n_p – концентрация дырок и электронов в полупроводнике p-типа, см^-3.

16. Скорость генерации генерации носителей заряда, 1/сек:

,

где r – коэффициент рекомбинации, см³/сек; n₀, p₀ – концентрации носителей заряда при отсутствии воздействия на полупроводник, см^-3; Δn, Δp – избыточные концентрации носителей заряда, см^-3.

17. Решение уравнения диффузии для одномерной полубесконечной системы при постоянстве граничной концентрации:

,

где Δn, Δp – избыточная концентрация носителей заряда в слое с координатой x=x₀, см^-3; L_n, L_p – диффузионная длина электронов, дырок, см.

18. Диффузионная длина носителей заряда, см:

,

где D_n, D_p - коэффициенты диффузии электронов, дырок, см²/сек; τ_n, τ_p – среднее время жизни носителей заряда, сек.

19. Дебаевская длина экранирования в собственном () и примесном () полупроводнике, см:

, ,

где e – заряд электрона, 1,6*10^-19 Кл; n_i – концентрация собственных носителей заряда, см^-3; n – концентрация ионизованной примеси, см^-3; k = 1,38·10^-23 Дж/град = 0,00008625 эВ/град – постоянная Больцмана; Т – абсолютная температура, град; ε – относительная диэлектрическая проницаемость, ед; ε₀ – абсолютная диэлектрическая проницаемость, 8,85*10^-12 Ф/м.

20. Проникновение поверхностного потенциала в полупроводник (при малом возмущении), В:

,

где - потенциал на поверхности полупроводника, В; x – координата по нормали к поверхности, м; L_Д – дебаевская длина экранирования, м.

21. Одномерное стационарное уравнение Шредингера:

или , ,

где - волновая функция, связанная с вероятностью нахождения частицы в точке x; E - полная энергия частицы, эВ; U – внешняя по отношению к частице потенциальная энергия, эВ; m – масса частицы, кг; ; h – постоянная Планка, h = 6,262·10^-34 Дж·c = 4,141·10^-15 эВ·c.

22. Вероятность нахождения частицы в пространственной области [x₁, x₂]:

,

где - волновая функция, связанная с вероятностью нахождения частицы в точке x; x₁, x₂ – пространственные пределы области (координаты границ), м.

23. Решение уравнения одномерного стационарного Шредингера для потенциальной ямы шириной L с бесконечно высокими стенками:

,

где n – номер квантованного состояния частицы в потенциальной яме, n=1,2, …; L – координатная ширина потенциальной ямы, м.

24. Рассеяние заряженной частицы на потенциальной ступеньке:

, ,

где T – коэффициент прохождения заряженной частицы потенциальной ступеньки, отн. ед; R – коэффициент отражения заряженной частицы от потенциальной ступеньки, отн. ед; E – энергия частицы, эВ; U₀ – высота потенциальной ступеньки, эВ.

25. Прохождение заряженной частицы через потенциальный барьер конечной ширины:

, , , ,

где T – коэффициент прохождения заряженной частицы потенциального барьера, отн. ед; R – коэффициент отражения заряженной частицы от потенциального барьера, отн. ед; U₁ – высота потенциального барьера, эВ; E < U₁ – энергия частицы, эВ; m – масса частицы, кг; h – постоянная Планка, h = 6,262·10^-34 Дж·c = 4,141·10^-15 эВ·c; L – координатная ширина потенциального барьера, м.