4.4. Условие пластичности анизотропных сред

Как уже отмечалось, поликристаллические металлы на макроскопическом уровне изотропны. Однако в результате обработки давлением поликристаллические металлы становятся анизотропными материалами, у которых свойства зависят от направления. Это так называемая деформационная анизотропия в отличие от начальной анизотропии кристалла. Одной из причин деформационной анизотропии является появление текстуры, т.е. системы закономерно ориентированных кристаллографических элементов большинства кристаллов (зерен), составляющих деформируемое тело.

В общем случае для анизотропного материала Мизесом в 1928 году было предложено следующее энергетическое условие начала пластичности:

,

где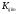- симметричный материальный тензор, отражающий анизотропию свойств.

Для ортотропного материала в главных осях анизотропии оно записывается следующим образом:

Мизес не сделал никаких предположений относительно коэффициентов К- и не выразил их через технические константы. В 1948 г. Хилл сделал следующую расшифровку условия Мизеса

Здесь X,Y,Z - пределы текучести при растяжении металла в главных направлениях анизотропии;

R,S,T - пределы текучести при сдвиге по отношению к главным осям.

Этим уравнением трудно пользоваться. Например, для листового проката практически не удается определить Z,R,S .

Арышенским Ю.М. в 1964 г. условие пластичности Мизеса предложено выразить в традиционной тензорной форме следующим образом:

; это условие, выраженное через деформационные показатели для

ортотропного тела, имеет вид:

.

Здесь - коэффициенты поперечной деформации, аналогичные

коэффициентам Пуассона, но только в пластической области. Первый индекс указывает направление поперечной деформации, а второй — направление действия силы. Их определяют при линейном напряженном состоянии (рис. 54).

Рис.54

главные оси анизотропии

При растяжении образцов в направлении 1

, .

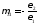Из условия постоянства объема

следует, что

или

.

Аналогично при одноосных испытаниях в направлениях 2 и 3 получаем

,

.

Коэффициент , получают при растяжении вырезанного образца

под углом 45° к осям 1 и 2, - между осями 2 и 3,- между осями 3 и 1.

В расчетах начала пластичности металла интенсивность напряжений удобно относить к главным осям анизотропии. Например, для первого

направления имеет вид

,

где - предел текучести металла в направлении 1.

По другим направлениям существуют следующие связи:

, .

Для ортотропной среды условие Мизеса интерпретируется эллиптическим равнонаклоненным к осям цилиндром. Для плоского

напряженного состояния () контур текучести имеет вид, показанный на рис. 55.

Рис. 55

В случае изотропного тела все = 0,5 и, принимает выражение

4.5. Экспериментальная проверка условий пластичности

Проверка обычно проводится в опытах по совместному растяжению продольной силой и кручению моментомтонкостенных труб ( Р+М— опыт) (рис. 56).

Рис. 56

Тогда напряженное состояние является плоским и осесимметричным и описывается тензором напряжений

,

где - осевое нормальное напряжение

,

- касательное напряжение,

,

- средний радиус тонкостенной трубы,

t - толщина ее стенки.

Инварианты тензора напряжений равны

Тогда кубическое уравнение для определения главных нормальных напряжений имеет вид

.

Его корни равны

,

Условие пластичности Треска - Сен-Венана примет

вид

или

.

В координатах (/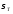),(/) это уравнения эллипсов с полуосями соответственно 1;0,5 и 1;(рис. 57).

Рис. 57