Глава 4. Теория пластичности

Изучению напряжений, деформаций и перемещений в пластически деформируемых телах посвящен раздел механики сплошных сред, называемый теорией пластичности. Теория пластичности решает главным образом те же задачи, что и теория упругости, но для материалов с другими физическими свойствами. Поэтому между указанными теориями имеется много общего. В частности, общими являются уравнения равновесия, геометрические уравнения, уравнения совместности деформаций. Только вместо обобщенного закона Гука, используемого в теории упругости, в теории пластичности применяются другие физические соотношения.

4.1. Условие перехода металла в пластическое состояние

Начало пластических деформаций является следствием перехода от одной формы устойчивого равновесия в атомной решетке зерна к другой. При линейном напряженном состоянии, например при растяжении, можно считать, что пластическое состояние наступает тогда, когда нагрузка вызывает нормальные напряжения, равные пределу текучести . Если по мере деформации металл упрочняется,

то для дальнейшего развития пластической деформации необходимо увеличить напряжение, величина которого определяется кривой упрочнения. Если упрочнение отсутствует, то пластическая деформация протекает при постоянном напряжении. Отсюда следует, что возникновение пластических деформаций однозначно определяется напряжениями.

Теперь требуется перенести эти рассуждения и на случай трехмерного (объемного) напряженного состояния. Сделать это значительно сложнее. Дело в том, что напряженное состояние в рассматриваемой точке описывается шестью компонентами тензора напряжений - ,,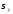,,,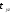. Количество возможных комбинаций напряжений, при которых тело переходит в пластическое состояние, является бесконечным. Точная форма поверхности раздела упругих и пластических деформаций неизвестна. В связи с этим приходится прибегать к гипотезам по переходу тела в пластическое состояние, а поверхность раздела строить на основе гипотез. Эти гипотезы и соответствующие уравнения, которые являются их математической формулировкой, называют критериями (условиями) пластичности. К ним предъявляются следующие требования:

Критерий пластичности должен иметь форму инварианта, так как характеризуется уравнением состояния тела, которое выражает некоторый физический закон. А это значит, что в это уравнение в качестве независимых переменных должны входить инварианты.

В уравнение критерия пластичности, помимо компонент тензора напряжений, должны входить компоненты материального тензора, характеризующие механические свойства металла и определяющие возникновение пластических деформаций при простейших напряженных состояниях.

Критерий пластичности должен быть действительным для любых элементарных объемов металла, находящихся в произвольном объемном напряженном состоянии.

Исходя из вышеприведенных требований для изотропного металла, критерий пластичности не должен зависеть от направлений и может бьггь представлен в виде функции инвариантов тензора напряжений:

,

где к - постоянная пластичности.

Как показывают опыты, при всестороннем равномерном растяжении или сжатии пластические деформации не возникают. Поэтому критерий пластичности можно представить как функцию только второго и третьего инвариантов девиатора напряжений:

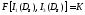
Если известны главные нормальные и максимальные касательные напряжения, то критерий пластичности можно записать в упрощенном виде:

или

Из многочисленных предложенных в разное время критериев пластичности наибольшее применение в обработке металлов давлением получили условия Треска и Мизеса. Рассмотрим их более подробно в той исторической последовательности, как они появились.