Методы и подходы неравновесной термодинамики, используемые при проведении анализа микро- и нанотехнологий и структур.

Теоретические сведения: «Методы и подходы неравновесной термодинамики, используемые при проведении анализа микро- и нанотехнологий и структур»

1. Элементы неравновесной термодинамики

а). Энтропия и необратимость физико-химических процессов

Термодинамическая система, находящаяся в равновесном состоянии, является «статичной», поскольку для нее не существует представления об ее эволюции во времени. Считается, что система когда-то перешла в это равновесное состояние из неравновесного состояния, при котором она была динамической системой и обладала «силами», которые приводили к различным изменениям ее состояния в части материального состава и структуры, и при этом постепенно подводили к ее закономерному финалу – термодинамическому равновесию. Эту тенденцию движения к состоянию равновесия можно избежать, если с помощью определенных внешних сил искусственно поддерживать систему в состоянии, далеком от термодинамического равновесия.

В неравновесной термодинамике понятия «сила» или «обобщенная сила» распространяется на все виды воздействия, включая и обычные механические силы. Эти силы, обусловленные наличием градиентов термодинамических параметров (концентрации, давления, химического или электрического потенциала и т.д.) могут поддерживать в системе постоянный приток или отток вещества и энергии. Таким образом, эти силы образуют потоки энергии или вещества, которые, в конце концов, истощают сами силы, их породившие. Все градиенты со временем постепенно исчезают (если не поддерживаются искусственным образом), и система достигает окончательного состояния термодинамического равновесия. Например, источник движущей силы в виде температурного градиента между двумя точками в объеме вещества порождает перенос какого-то количества теплоты Q из горячей части системы в холодную. Этот поток теплоты увеличивает температуру холодного участка за счет охлаждения горячего участка, что постепенно приводит систему к состоянию теплового равновесия.

Наличие сил и потоков в неравновесной системе означает, что эта система неоднородна по своему составу и что в ней происходят различные физико-химические процессы. Поэтому в наиболее общем случае состав и все соответствующие переменные системы изменяются в пространстве и во времени. Возникает вопрос, каким же образом в неравновесных системах могут быть определены интенсивные параметры (подобные температуре или давлению), если они являются функцией координат и, вообще то, введены в рассмотрение исходя из представлений о равновесном характере системы. Эти трудности могут быть преодолены, если воспользоваться представлением о локальном равновесии системы. В этом случае, вся макроскопическая система условно расчленяется на совокупность большого количества локальных подсистем (остающихся по своей сути макроскопическими объектами) таким образом, что можно считать, что каждая отдельная подсистема находится в состоянии термодинамического равновесия (т.е. внутри ее термодинамические параметры сохраняют неизменное значение).

Примем допущение, что все выводы равновесной термодинамики могут быть применены к локально определяемым параметрам небольшого элементарного объема. Локальные переменные принято относить к единице массы вещества. Но удобнее перейти к переменным, соотнеся их к объему системы. Тогда, если — парциальная масса на единицу объема (парциальная плотность) -го компонента, то полная плотность , удельная энтропия и удельная внутренняя энергия , (отнесенные к единице объема среды) определяются выражениями [5]:

	;	(1.а)
	;	(1.б)
	,	(1.в)

где и - соответственно удельные энтропия и внутренняя энергия единицы объема компонента вещества - типа.

Согласно принятой гипотезе, относительно правомерности использования принципа локального равновесия применительно к термодинамической системе в целом, параметры локальных подсистем, определяемые с помощью выражений (1), по своей природе становятся аналогичными обычным параметрам, характеризующих равновесное состояние термодинамической системы. Таким образом, для каждого малого объема неравновесной термодинамической системы, его локальная энтропия может быть связана с локальной энергией и парциальной массой соотношением, которое является частным случаем известного уравнения Гиббса:

,

(2)

где - химический потенциал единицы объема компонента вещества - типа.

Согласно выражению (1.б) общая энтропия термодинамической системы, имеющей объем , будет равна:

.

(3)

Выше был продемонстрирован общий подход теоретического анализа неравновесной системы. Если термодинамическая система является пространственно-неоднородной по какому то либо термодинамическому параметру, то необходимо предварительно определить функцию распределения для этого параметра, а затем проводить интегрирование выражения (3) по всему объему термодинамической системы.
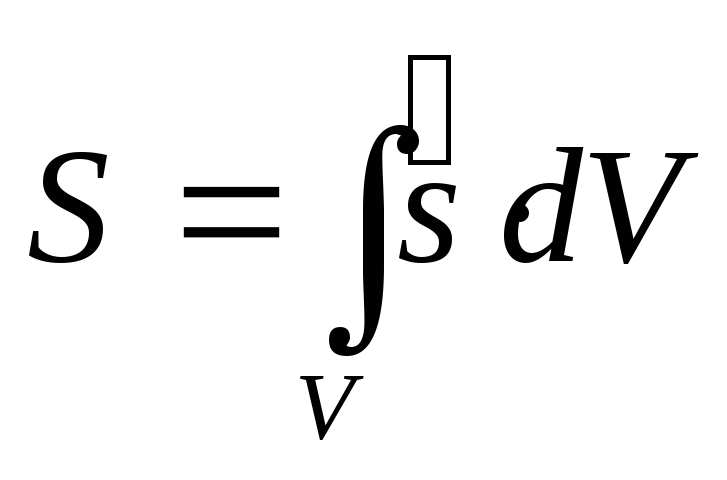