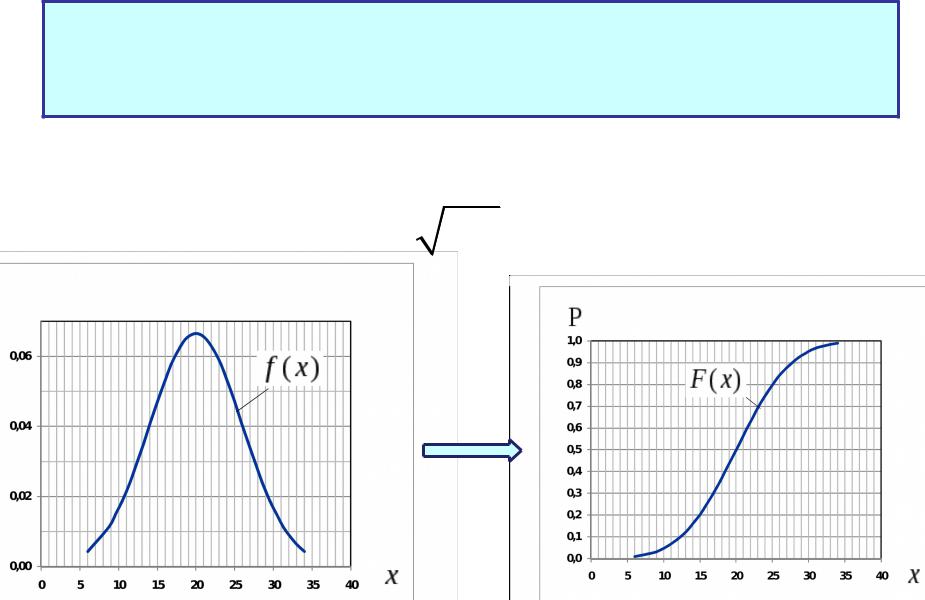
Функция распределения нормального закона распределения
|
x |
|
|
|
1 |
|
x |
|
(x mx ) |
2 |
|
F(x) |
|
f (x)dx |
|
|
|
|
exp |
|
dx |
||
|
|
|
|
|
|||||||
|
|
x |
|
|
|
2 |
|
|
|||
|
|
|
|
2 |
|
2 x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) P(X x) |
. Д у п л я к и н |
11 |
|
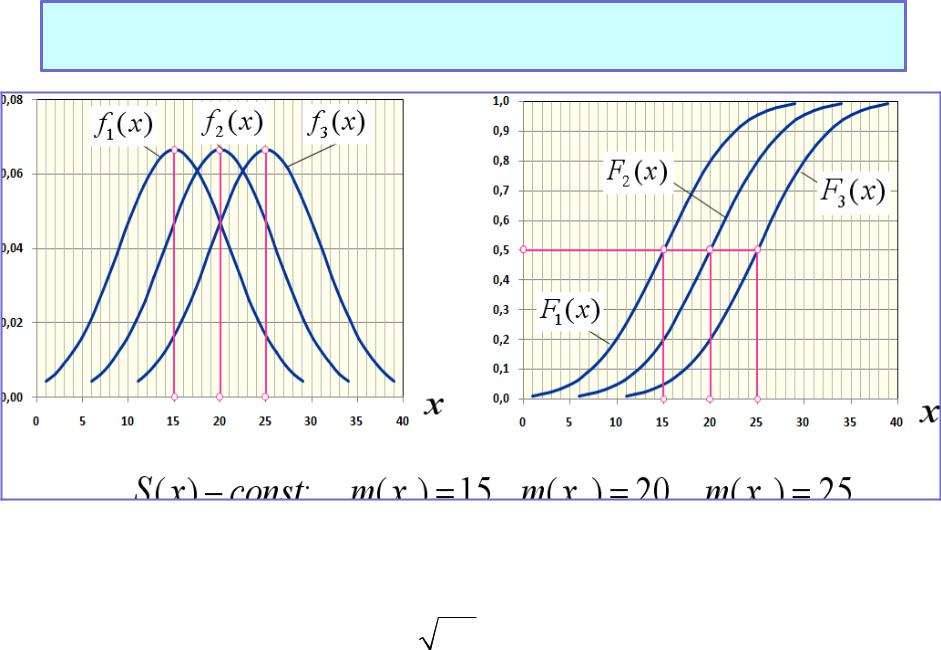
Параметрическая вариация нормального закона
|
x |
|
|
1 |
|
x |
|
(x mx ) |
2 |
|
F(x) |
|
f (x)dx |
|
|
|
exp |
|
dx |
||
|
|
|
|
|||||||
|
|
x |
|
|
|
2 |
|
|
||
|
|
|
|
2 |
|
2 x 12 |
|
|||
Д у п л я к и н
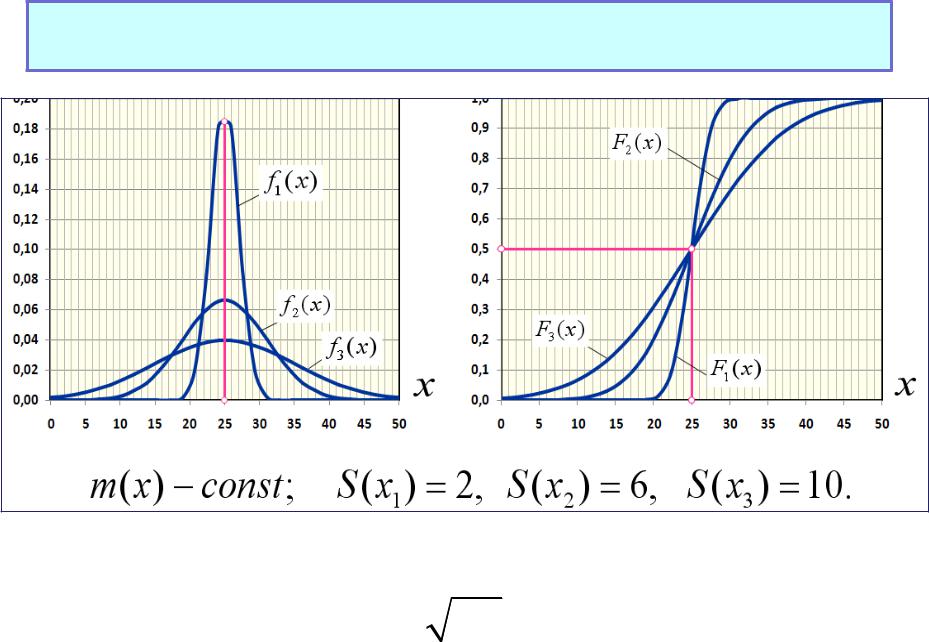
Параметрическая вариация нормального закона
|
x |
|
|
1 |
|
x |
|
(x mx ) |
2 |
|
F(x) |
|
f (x)dx |
|
|
|
exp |
|
dx |
||
|
|
|
|
|||||||
|
|
x |
|
|
|
2 |
|
|
||
|
|
|
|
2 |
|
132 x |
|
|
||
Д у п л я к и н
Построение функции распределения нормального закона
F(x) P(X x)
|
x |
|
|
1 |
|
x |
|
(x mx ) |
2 |
|
F(x) |
|
f (x)dx |
|
|
|
exp |
|
dx |
||
|
|
|
|
|||||||
|
|
x |
|
|
|
2 |
|
|
||
|
|
|
|
2 |
|
2 x |
|
|
||
Интеграл невозможно взять аналитически !
Д у п л я к и н |
14 |
|
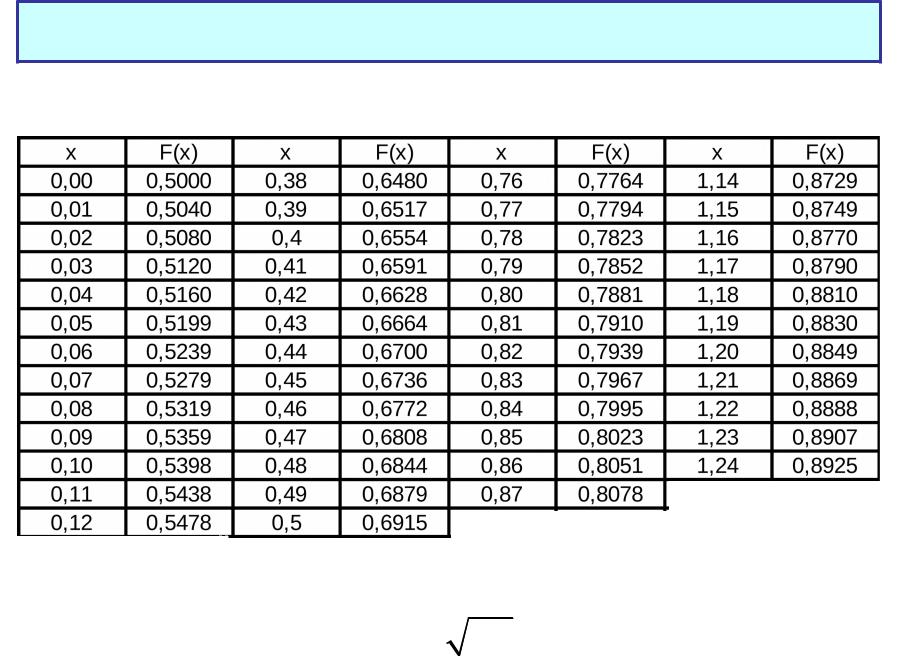
Таблицы стандартизованного нормального распределения
F(x) : mx 0; |
x2 1 |
|
|
x |
|
|
1 |
|
x |
|
(x mx ) |
2 |
|
|
|
F(x) |
|
f (x)dx |
|
|
|
exp |
|
dx |
|
||
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||
|
|
|
x |
|
|
|
2 |
|
|
|||
|
|
|
|
|
2 |
|
152 x |
|
|
|||
. Д у п л я к и н |
|
|
|
|
|
|
|
|
|
|
||
Задача 1. |
P(X X P ) P X P |
Используя таблицы стандартизованного нормального распределения, при заданных значениях mx ≠ 0, sx ≠ 1 найти
значение хр, ниже которого данная случайная величина может реализовываться с вероятностью Р.
Решение
1.По таблицам стандартизованного нормального распределения находим для заданной вероятности Р
хтабл(Р), которое обозначим up = хтабл(Р). up – называется квантиль распределения.
2. Вычислим искомое значение
хр= mx+ upsx .
16
. Д у п л я к и н
Задача 2. X P P(X X P ) P
Используя таблицы стандартизованного нормального распределения, найти значение вероятности Р с которой данная случайная величина может реализовываться со значениями меньше заданного х при известных mx≠0, sx≠1.
Решение
1.Вычислим квантиль up=(х – mx)/ sx.
2.По таблицам стандартизованного нормального распределения находим искомую вероятность Р
Р= Pтабл(xтабл=up).
. Д у п л я к и н |
17 |
|
Вопрос: Как быть, если в используемой таблице нет отрицательных квантилей?
Пример. |
mx 5; |
sx 3. |
P(X 1,40) ? |
|
Решение. |
up 1,40 5 |
1,20. |
||
|
|
3 |
|
|
Отрицательные аргументы в таблицах нормального стандартного распределения обычно не приводятся.
. Д у п л я к и н |
18 |
|
Воспользуемся свойством центральной симметрии функции нормального распределения
P(X 1,4) F станд (1,4 5) F станд ( 1,20) 1 F станд ( 1,20) 1 0,8849 0,1151 |
|||
норм |
3 |
норм |
норм |
|
|
|
|
М . Д у п л я к и н |
19 |
|
Правило “трёх сигма”
Если случайная величина, подчиняющаяся нормальному закону распределения, зарегистрирована за пределами интервала
(mx 3 Sx ; mx 3 Sx ) ,
то такое значение признаётся ошибочно зарегистрированным и изымается из последующего статистического анализа.
20
Д у п л я к и н