Достоверное событие – это событие, которое в результате опыта обязательно произойдёт.
Например, если В – достоверное событие, то
Р(В)=1.
М . Д у п л я к и н |
11 |
|
Невозможное событие – это событие, которое в результате опыта в принципе не может произойти.
Например,
если F – невозможное событие, то
Р(F)=0.
М . Д у п л я к и н |
12 |
|
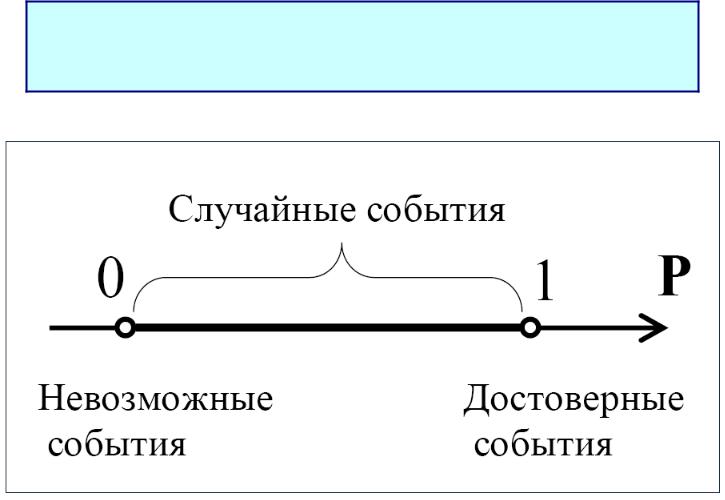
Шкала вероятностей
М . Д у п л я к и н |
13 |
|
Пример 1.
События:
А1 – получение отличной отметки по теории вероятностей.
А2 – получение положительной отметки по теории вероятностей.
Вероятности: Р(А1)=0,45; Р(А2)=0,70.
Вывод: событие А2 более вероятно, чем событие А1.
Примечание. Вывод тривиальный, т.к. он не вызывал никаких сомнений.
М . Д у п л я к и н |
14 |
|
Пример 2.
События:
B1 – убытки при реализации проекта №1.
B2 – убытки при реализации проекта №2.
Вероятности: Р(B1)=0,35; Р(B2)=0,15.
Вывод: Проект №1 более рискованный, чем проект №2.
М . Д у п л я к и н |
15 |
|
ПОЛНАЯ ГРУППА СОБЫТИЙ
Если в результате опыта должно произойти хотя бы одно из известной группы событий, то эта совокупность событий представляет собой полную группу событий.
. Д у п л я к и н |
16 |
|
НЕСОВМЕСТНЫЕ СОБЫТИЯ
События в данном опыте называются несовместными, если никакие два из них не могут появиться вместе.
М . Д у п л я к и н |
17 |
|
РАВНОВОЗМОЖНЫЕ СОБЫТИЯ
Если по условиям опытов нет оснований считать, что какое–либо событие из рассматриваемой группы событий является более или менее возможным, то события такой группы называются равновозможными.
Примечание. Равновозможные события имеют одинаковые вероятности.
Пример. «Орёл» или «решка» при подбрасывании монеты.
18
Д у п л я к и н
СЛУЧАИ (ШАНСЫ)
Случаи или шансы – это результаты реализации группы событий при одновременном выполнении следующих условий:
-Полная группа событий.
-Несовместные события.
-Равновозможные события.
. Д у п л я к и н |
19 |
|
НЕПОСРЕДСТВЕННЫЙ ПОДСЧЁТ ВЕРОЯТНОСТЕЙ
При реализации событий по схеме случаев вероятность интересующего нас
события А вычисляется по формуле
P(A)= mn ,
где n – общее число случаев,
m – число случаев, приводящих (благоприятствующих) к появлению события А .
20
Д у п л я к и н