МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИС

Отчет

по практической работе №5

по дисциплине «ИКСиС»

Тема: 1-я и 2-я формулы Эрланга

Вариант №24

Студент гр. 1371		Татанов С.М.
Преподаватель		Воробьев А.И. Верзун Н.А.

Санкт-Петербург

2023

Цель работы:

Написать программу, рекуррентно реализующую первую формулу Эрланга. Построить графики зависимости вероятности блокировки заявок от интенсивности поступающей нагрузки при числе обслуживающих устройств 2 * n. Построить графики зависимости вероятности блокировок заявок от числа обслуживающих устройств при интенсивности поступающей нагрузки n.

Написать программу расчёта второй формулы Эрланга. Построить графики зависимости вероятности ожидания начала обслуживания и средней длины очереди от интенсивности поступающей нагрузки при числе обслуживающих устройств 2 * n. Построить графики зависимости вероятности ожидания начала обслуживания и средней длины очереди от числа обслуживающих устройств при интенсивности поступающей нагрузки n.

Исходные данные:

n - число обслуживающих устройств = 24*2 = 48

A - интенсивность поступающей нагрузки = 24

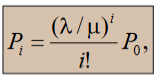
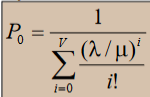
Первая формула Эрланга

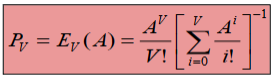
Вторая формула Эрланга

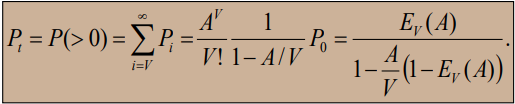
from matplotlib import pyplot as plt

 def graph(x, y, x_label, y_label, title):

plt.plot(x, y)

plt.xlabel(x_label)

plt.ylabel(y_label)

plt.grid(True)

plt.title(title)

plt.show()

 def erl1(A, n):

a = 1

v = 1

s = 0

for j in range(0, n):

a = a * A

v = v * (n + 1)

e = a / v

s += e

res = a / v

res = res / s

return res

 

 

x = []

y = []for i in range(1, 100):

x.append(i)

y.append(erl1(i, 48))

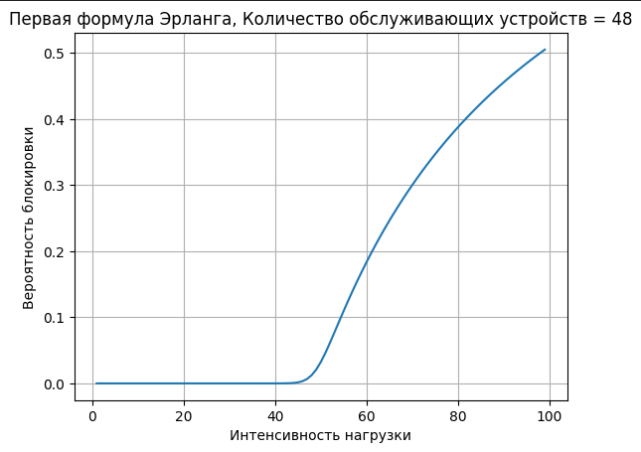
graph(x, y, "Интенсивность нагрузки",

"Вероятность блокировки", "Первая формула Эрланга, Количество обслуживающих устройств = 48")

x = []

y = []for i in range(1, 100):

x.append(i)

y.append(erl1(24, i))

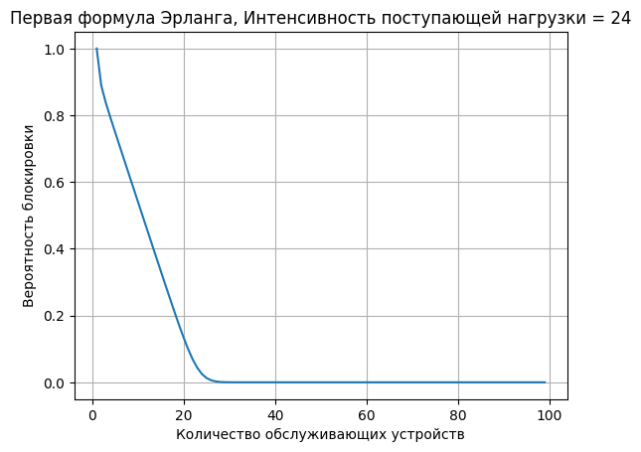
graph(x, y, "Количество обслуживающих устройств",

"Вероятность блокировки", "Первая формула Эрланга, Интенсивность поступающей нагрузки = 24")

 

from matplotlib import pyplot as plt

 def graph(x, y, x_label, y_label, title):

plt.plot(x, y)

plt.xlabel(x_label)

plt.ylabel(y_label)

plt.grid(True)

plt.title(title)

plt.show()

 def erl1(A, n):

a = 1

v = 1

s = 0

for j in range(0, n):

a = a * A

v = v * (n + 1)

e = a / v

s += e

res = a / v

res = res / s

return res

 

 

x = []

y = []for i in range(1, 100):

x.append(i)

y.append(erl1(i, 48))

graph(x, y, "Интенсивность нагрузки",

"Вероятность блокировки", "Первая формула Эрланга, Количество обслуживающих устройств = 48")

x = []

y = []for i in range(1, 100):

x.append(i)

y.append(erl1(24, i))

graph(x, y, "Количество обслуживающих устройств",

"Вероятность блокировки", "Первая формула Эрланга, Интенсивность поступающей нагрузки = 24")

 

from matplotlib import pyplot as plt

 def graph(x, y, x_label, y_label, title):

plt.plot(x, y)

plt.xlabel(x_label)

plt.ylabel(y_label)

plt.grid(True)

plt.title(title)

plt.show()

 def erl1(A, n):

a = 1

v = 1

s = 0

for j in range(0, n):

a = a * A

v = v * (n + 1)

e = a / v

s += e

res = a / v

res = res / s

return res

 

 

x = []

y = []for i in range(1, 100):

x.append(i)

y.append(erl1(i, 48))

graph(x, y, "Интенсивность нагрузки",

"Вероятность блокировки", "Первая формула Эрланга, Количество обслуживающих устройств = 48")

x = []

y = []for i in range(1, 100):

x.append(i)

y.append(erl1(24, i))

graph(x, y, "Количество обслуживающих устройств",

"Вероятность блокировки", "Первая формула Эрланга, Интенсивность поступающей нагрузки = 24")

 

from matplotlib import pyplot as plt

def graph(x, y, x_label, y_label, title):

plt.plot(x, y)

plt.xlabel(x_label)

plt.ylabel(y_label)

plt.grid(True)

plt.title(title)

plt.show()

def erl1(A, n):

a = 1

v = 1

s = 0

for i in range(0, n):

a = a * A

v = v * (n + 1)

e = a / v

s += e

res = a / v

res = res / s

return res

x = []

y = []

for i in range(1, 100):

x.append(i)

y.append(erl1(i, 48))

graph(x, y, "Интенсивность нагрузки", "Вероятность блокировки", "Первая формула Эрланга, Количество обслуживающих устройств = 48")

x = []

y = []

for i in range(1, 100):

x.append(i)

y.append(erl1(24, i))

graph(x, y, "Количество обслуживающих устройств", "Вероятность блокировки", "Первая формула Эрланга, Интенсивность поступающей нагрузки = 24")

from matplotlib import pyplot as plt

def graph(x, y, x_label, y_label, title):

plt.plot(x, y)

plt.xlabel(x_label)

plt.ylabel(y_label)

plt.grid(True)

plt.title(title)

plt.show()

def erl1(A, n):

a = 1

v = 1

s = 0

for i in range(0, n):

a = a * A

v = v * (n + 1)

e = a / v

s += e

res = a / v

res = res / s

return res

def erl2(A, n):

x = erl1(A, n)

y = 1 - x

z = A / n

y = z * y

y = 1 - y

return x / y

def queueLength(A, n):

x = (A * erl1(A, n)) / ((n - A) + A * erl1(A, n))

v = n / (n - A)

return x * v

x,y1,y2 = [],[],[]

for i in range(1, 47):

x.append(i)

y2.append(queueLength(i, 48))

y1.append(erl2(i, 48))

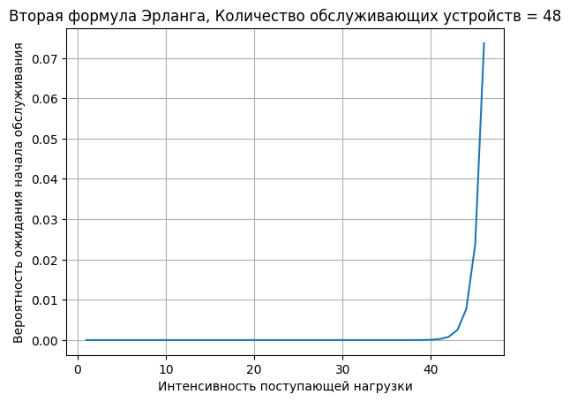
graph(x, y1, "Интенсивность поступающей нагрузки", "Вероятность ожидания начала обслуживания", "Вторая формула Эрланга, Количество обслуживающих устройств = 48")

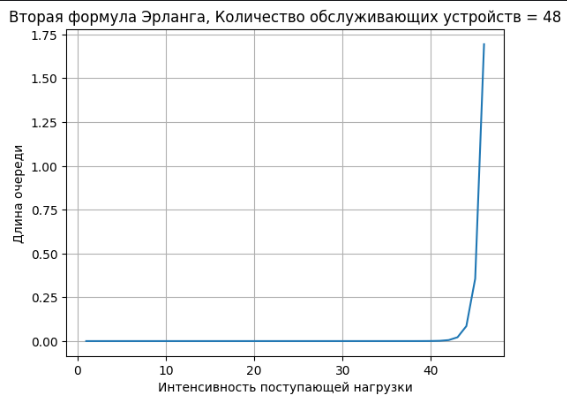
graph(x, y2, "Интенсивность поступающей нагрузки", "Длина очереди", "Вторая формула Эрланга, Количество обслуживающих устройств = 48")

x,y1,y2 = [],[],[]

for i in range(25, 100):

x.append(i)

y2.append(queueLength(24, i))

y1.append(erl2(24, i))

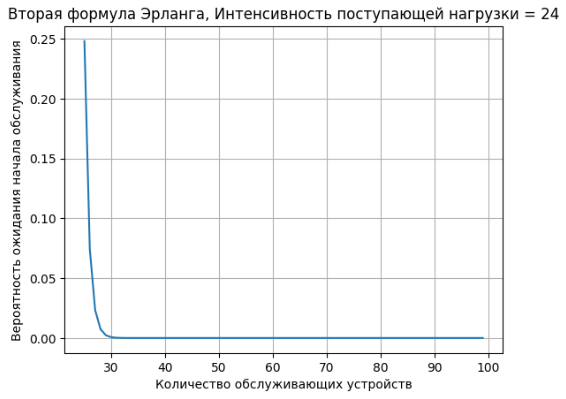
graph(x, y1, "Количество обслуживающих устройств", "Вероятность ожидания начала обслуживания", "Вторая формула Эрланга, Интенсивность поступающей нагрузки = 24")

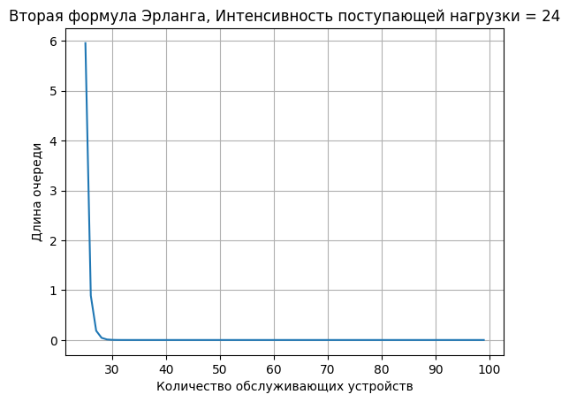
graph(x, y2, "Количество обслуживающих устройств", "Длина очереди", "Вторая формула Эрланга, Интенсивность поступающей нагрузки = 24")

Вывод

После изучения первой и второй формулы Эрланга и реализации программ была изучена зависимость вероятности блокировки и длины очереди заявок от количества рабочих станций и от интенсивности потока. Построены графики этих зависимостей.

Вероятность блокировки увеличивается если устройств становится меньше чем заявок. Длина очереди заявок пропорциональна вероятности блокировки.