ФГБОУ ВО НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
«МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ»
Кафедра Управления и интеллектуальных технологий
Лабораторная работа № 3
“ Исследование устойчивости нелинейной САУ”
Курс: Теория автоматического управления
Выполнили:
Болотникова А.А.
Акиньшин А.В.
Группа: А-03-20
Бригада 1
Проверил:
Дементьев В.Ю.
Москва, 2023
Выполнение работы
Цель работы - закрепление знаний по исследованию нелинейных систем автоматического регулирования на основании критерия Попова и методом гармонической линеаризации.
Исходные данные для варианта 1:
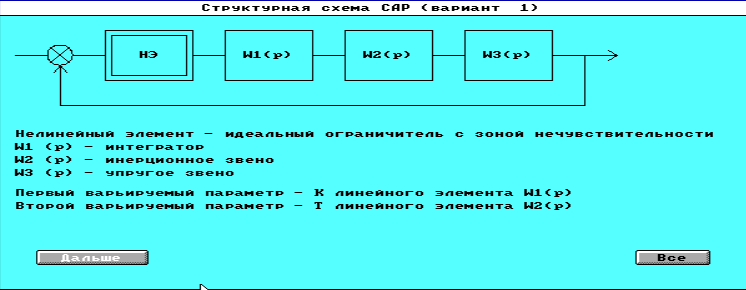
рис. 1 структура САР для варианта 1
рис. 2 заданные характеристики звеньев
рис. 3 релейная характеристика с зоной нечувствительности
1.1. Определить границу области устойчивости в пространстве двух варьируемых параметров САУ, отмеченных в табл. 5.1. Зафиксировать в протокол график АФХ модифицированной линейной части системы для двух различных точек
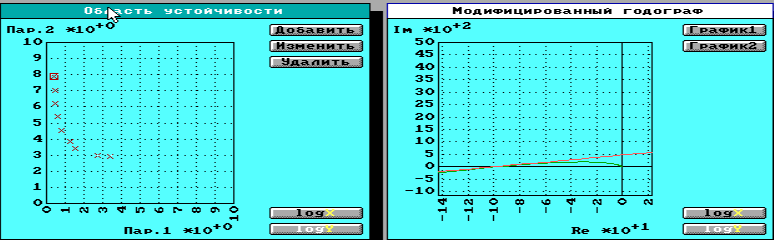
рис. 4 точка, соответствующая границе устойчивости
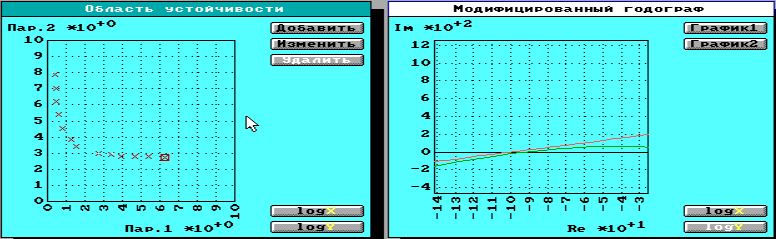
рис. 5 точка, соответствующая границе устойчивости
Путем подбора варьируемых параметров подобрали несколько значений при которых система является устойчивой. Для проверки устойчивости выполнялась проверка по критерию Гелига так как исследуется нейтрально устойчивая ЛЧ и НЭ с зоной нечувствительности.
2. Заданную нелинейную САУ исследовать методом гармонической линеаризации.
2.1. Для нелинейного элемента исследуемой САУ построить годограф эквивалентного комплексного коэффициента усиления Wнэ(А).
рис. 6 ЭККУ НЭ от амплитуды входного сигнала
рис.
7 окно задания типов характеристик
рис. 8 годографы нелинейной части и линейной части
По методу Гольдфарба видно, что обратная характеристика НЭ пересекает годограф линейной части «изнутри наружу», что говорит о наличии устойчивых автоколебаний в этой точке.
2.2.
На основании анализа расположения на
комплексной плоскости годографа линейной
части системы
и эквивалентного комплексного
коэффициента усиления нелинейного
элемента
,
определить границу области отсутствия
автоколебаний в пространстве двух
параметров, отмеченных в таблице 5.1.
рис. 9 выбор решения (частота и амплитуда)
рис. 10 точка, соответствующая отсутствию автоколебаний
рис. 11 точка, соответствующая отсутствию автоколебаний
рис. 12 точка, соответствующая отсутствию автоколебаний
На полученных графиках видно, что обратная характеристика НЭ не пересекает годограф линейной части, а это говорит нам об отсутствии автоколебаний.
рис. 13 точка, соответствующая наличию автоколебаний
На полученном графике видно, что при данных значениях переменных параметров будут наблюдаться автоколебания.
3. Исследовать НСАУ путем численного моделирования процессов на ПК.
3.1. Определить параметры автоколебаний в системе.
рис. 14 график автоколебаний
рис.
15 график автоколебаний
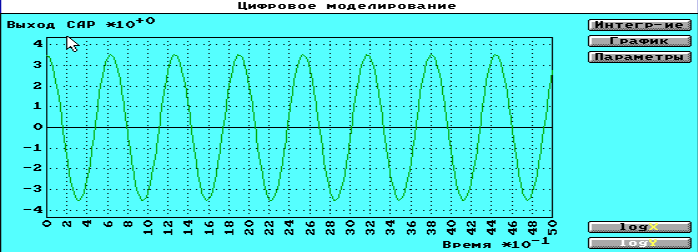
Параметры автоколебаний в системе:
3.2. Определить границу области устойчивости НСАУ в пространстве двух параметров.
рис. 16 точка, соответствующая затухающим колебаниям
рис. 17 точка, соответствующая затухающим колебаниям
По полученным графикам видно, что при значениях переменных параметров, находящихся ниже границы устойчивости, в системе наблюдаются затухающие колебания.
4. Провести сравнительный анализ результатов исследования НСАУ различными методами.
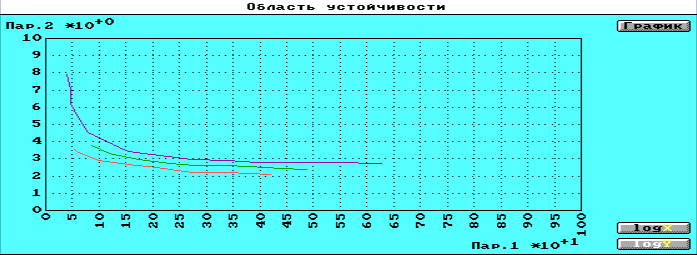
рис. 18 график, содержащий в себе границу устойчивости системы, границу отсутствия автоколебаний и границу затухающих колебаний
Вывод: из проведенных исследований устойчивости НСАУ следует, что в системе отсутствуют автоколебания при значениях переменных параметров, которые меньше значений переменных параметров на границе устойчивости. Для определения границы устойчивости был использован критерий Гелига, а для проверки отсутствия АК применялся метод гармонического баланса.