2. Случайные величины и случайные векторы

2.1. Случайные величины. Законы распределения и числовые характеристики

Пусть - вероятностное пространство.Случайной величиной называется функция , являющаяся измеримой относительно-алгебры, то есть такая функция, что для любого действительного

Функцией распределения случайной величины называется функция, при каждомопределяемая равенством

Основные свойства функции распределения:

1) для любого;

2) неубывающая;

3) непрерывная слева:для любого;

4)

5) Для любых

6) , где- скачок функции распределения в точке.

Случайная величина называется дискретной, если множество ее возможных значений конечно или счетно.

Закон распределения дискретной случайной величины (дискретное распределение) задается в виде ряда (таблицы) распределения:

в которой - значения случайной величины,, () - вероятности, с которыми эти значения принимаются. При этом выполняетсяусловие нормировки:

.

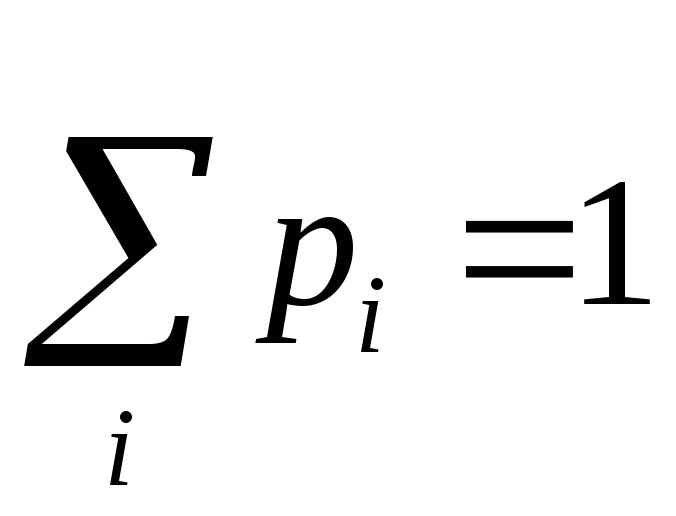Функция распределения дискретной случайной величины определяется формулой:

.

Случайная величина называетсянепрерывной (имеющей непрерывный закон распределения или просто непрерывное распределение), если существует функция такая, что для любогофункция распределениядопускает представление:

.

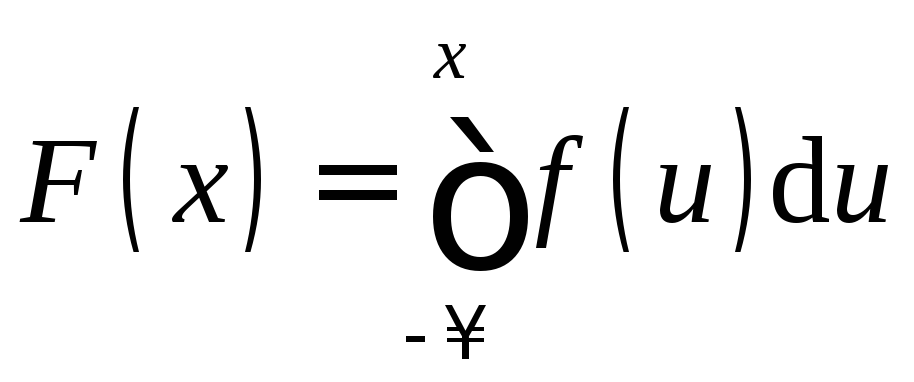При этом функция называетсяплотностью вероятностей (плотностью распределения вероятностей, плотностью распределения) случайной величины .

Если случайная величина является непрерывной, то ее функция распределения всюду непрерывна и для почти всехдифференцируема. При этом почти всюду (в точках непрерывности плотности вероятностей) имеет место равенство:

.

Свойства плотности вероятностей:

1) для любого;

2) 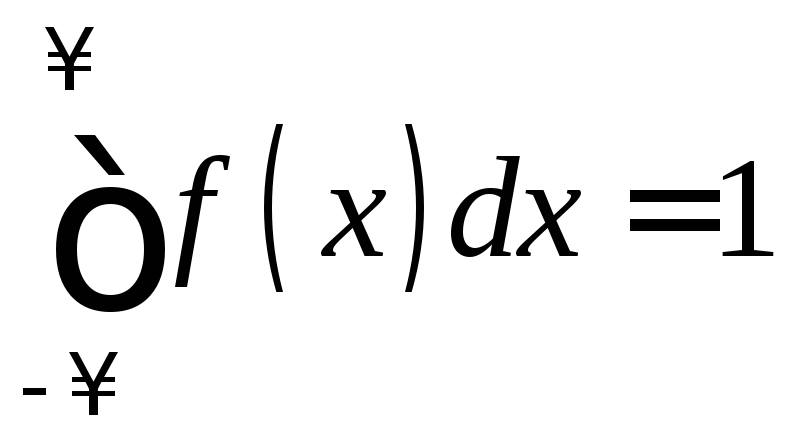- условие нормировки;

3) Для любых

.

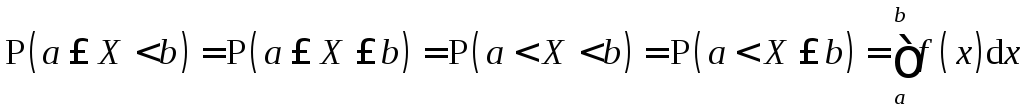Математическим ожиданием (средним значением) случайной величины , имеющей функцию распределения, называется число

,

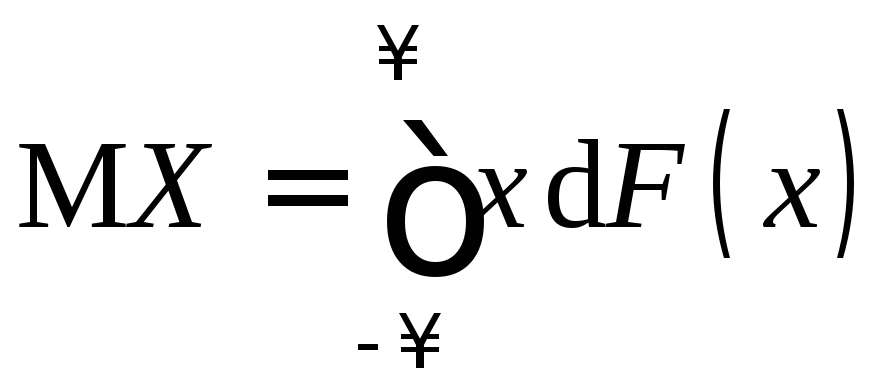если этот интеграл сходится абсолютно. Если интеграл не сходится абсолютно, то говорят, что у случайной величины математическое ожидание не существует.

Для дискретной случайной величины, принимающей значения с вероятностями, математическое ожидание определяется формулой:

,

а для непрерывной случайной величины с плотностью вероятностейформула для математического ожидания имеет вид:

.

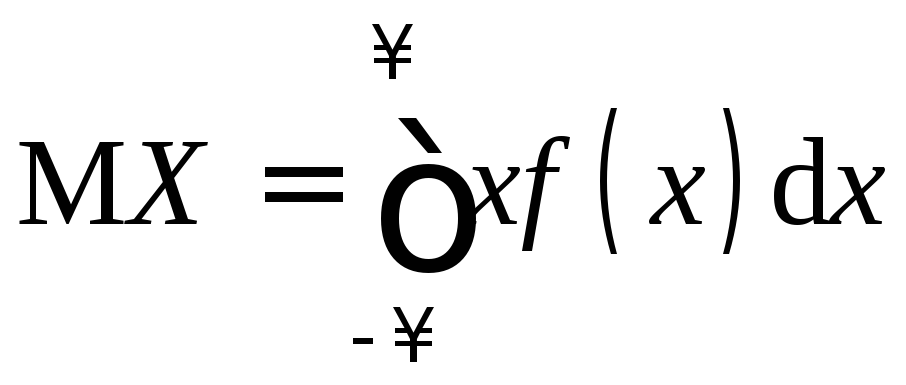Дисперсией случайной величины называется число

.

Для дисперсии также справедливо выражение:

.

Формулы для вычисления дисперсии :

- если - дискретная случайная величина, то

- если - непрерывная случайная величина, то

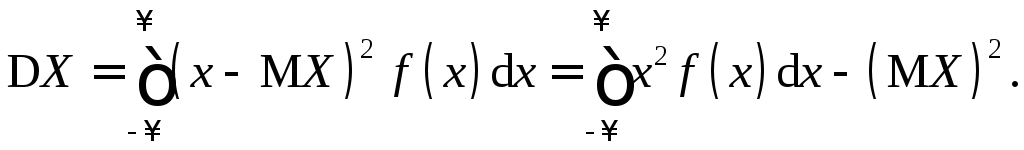
Число называетсясредним квадратическим отклонением случайной величины .

Величина называется начальным моментом - го порядкаслучайной величины , а величина-центральным моментом - го порядка. Очевидно, что

Вычисляются начальные и центральные моменты по формулам:

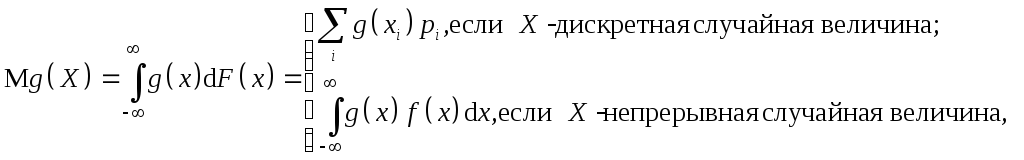в которых функция илисоответственно.

Величина , определяемая равенством, называется-квантилем распределения случайной величины . Квантильназываетсямедианой распределения случайной величины .

Модой распределения непрерывной случайной величины называется число, при котором плотность вероятностейдостигает максимального значения. Распределения с одной модой называются унимодальными, а распределения с несколькими модами – мультимодальными.

Основные законы распределения случайных величин приведены в Таблице П4.

Пример 1. Дискретная случайная величина принимает значения –1, 0, 1 с вероятностями, соответственно равными. Написать выражение и построить график функции распределения, определить вероятность, найти математическое ожиданиеи дисперсию.

Решение. Закон распределения случайной величины имеет вид:

	-1	0	1
				.

Аналитическое выражение для функции распределения случайной величины задается формулой:

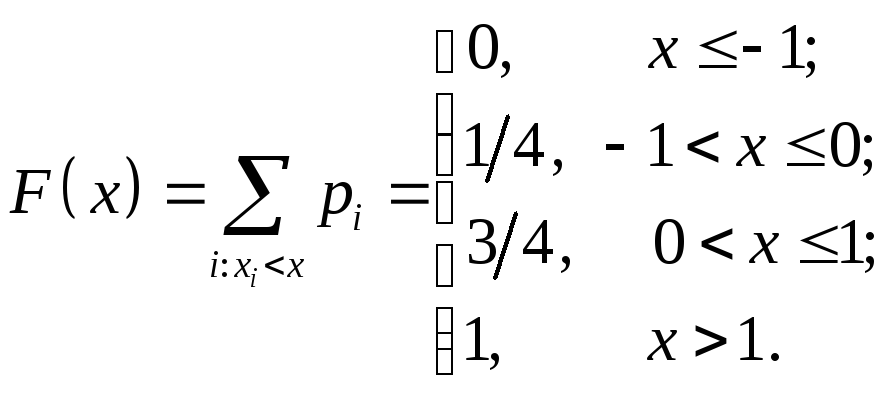
График функции распределения имеет вид:

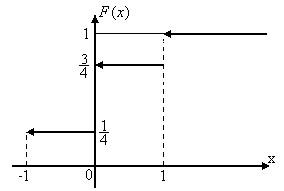
Рис. 2.1.

,

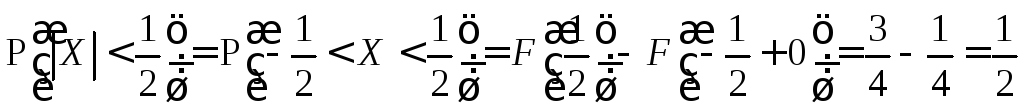или иначе .

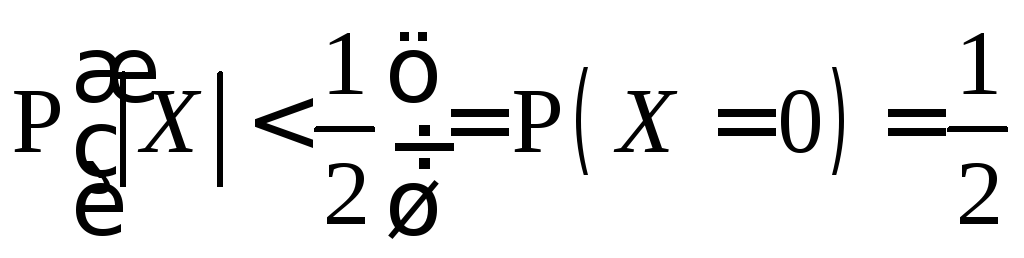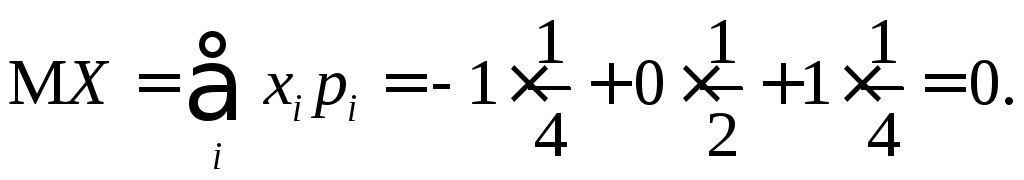
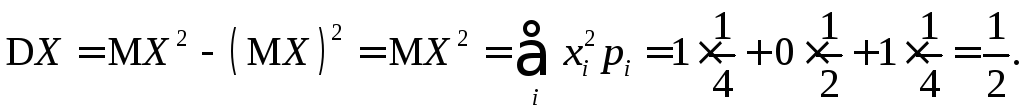
Пример 2. Непрерывная случайная величина имеет плотность вероятностей, график которой изображен на рисунке 2.2 (закон распределения прямоугольного треугольника):

Найти:

а) выражение для плотности вероятностей и параметр ;

б) функцию распределения и построить ее график;

в)

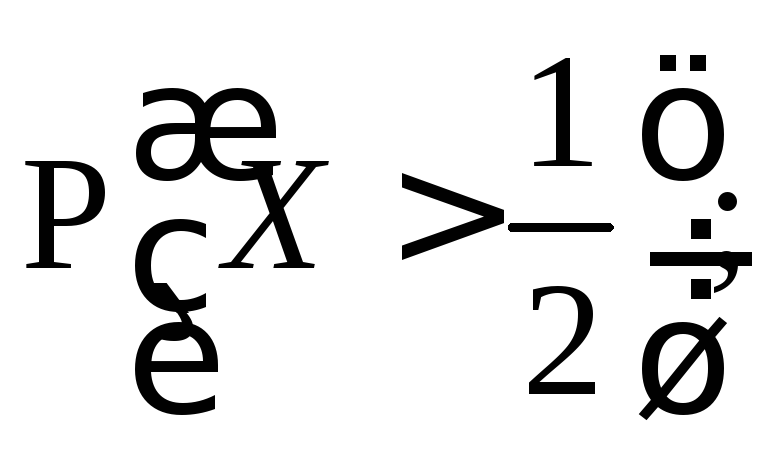
г) и.

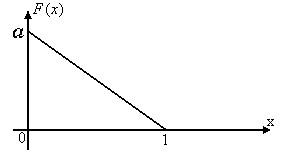
Рис. 2.2.

Решение. Аналитическое выражение для плотности вероятностей имеет вид:

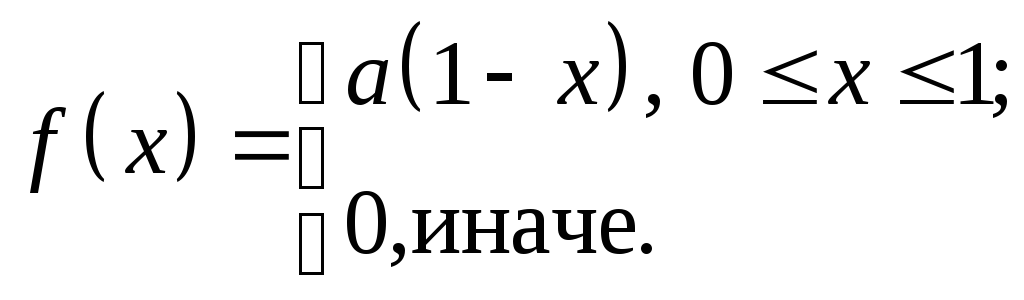
Неизвестный параметр находится из условия нормировки:

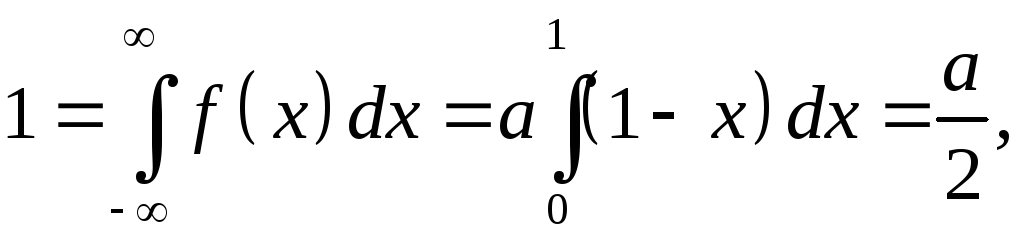откуда

Замечание. В данном случае параметр проще найти из геометрических соображений. Из условия нормировки следует, что площадь под графиком плотности вероятностей равна 1, то естьоткуда.

Аналитическое выражение для функции распределения случайной величины задается формулой:

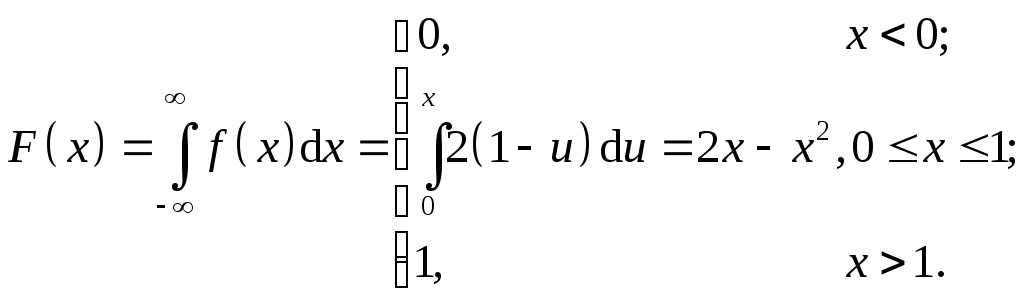
График функции распределения имеет вид:

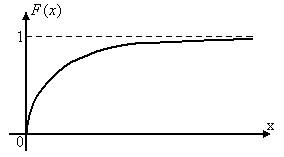
Рис. 2.3.

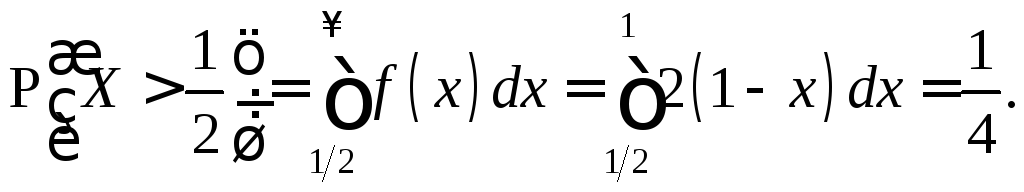
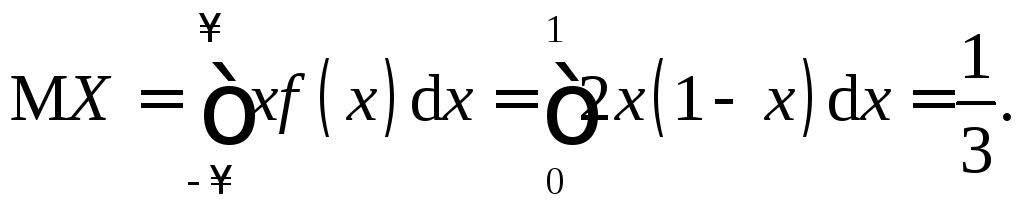
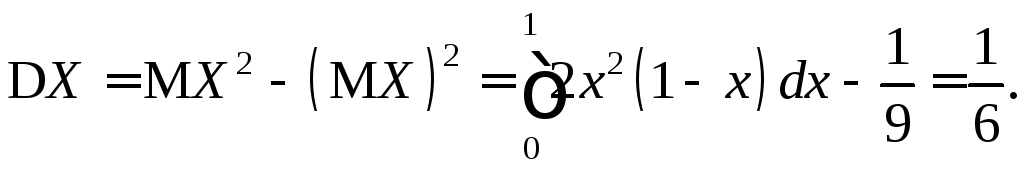
Задачи

2.1.1. Дан график функции распределения случайной величины(см. рис. 2.4).

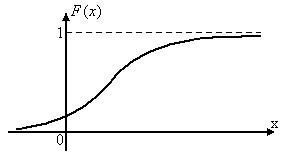
Рис.2.4.

Как изменится этот график, если:

а) прибавить к случайной величине 1;

б) вычесть из случайной величины 2;

в) умножить случайную величину на 2;

г) изменить знак случайной величины на противоположный?

2.1.2. Дан график плотности вероятностей случайной величины(см. рис. 2.5).

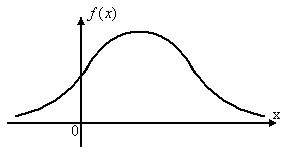
Рис. 2.5.

Как изменится этот график, если:

а) прибавить к случайной величине 1;

б) вычесть из случайной величины 2;

в) умножить случайную величину на 2;

г) изменить знак случайной величины на противоположный?

2.1.3. Может ли функция быть функцией распределения случайной величины принимающей значения из интервала:

а) б)в)?

2.1.4. К случайной величине прибавили постоянную, неслучайную величину. Как от этого изменятся ее характеристики:

1. математическое ожидание;

2. дисперсия;

3. среднее квадратическое отклонение;

4. второй начальный момент?

2.1.5. Случайную величину умножили на постоянную, неслучайную величинуКак от этого изменятся ее характеристики:

1) математическое ожидание;

2) дисперсия;

3) среднее квадратическое отклонение;

4) второй начальный момент?