Введение

Настоящий сборник задач представляет собой обобщение ряда методических разработок, изданных на факультете информатики Самарского государственного аэрокосмического университета за последние 20 лет. В сборнике приведено свыше 600 задач различной степени сложности по всем разделам теории вероятностей, которые изучаются в университетском курсе «Теория вероятностей и математическая статистика» при подготовке бакалавров по направлению «Прикладная математика и информатика».

Весь материал разбит на три раздела, каждый раздел – на подразделы, в зависимости от тематики и методов решения задач.

Каждый подраздел начинается с теоретических сведений, необходимых при решении представленных задач. Затем приводятся наиболее важные типовые задачи с решениями. Подборка задач в подразделах произведена «гнездовым» методом, при котором однотипные задачи располагаются рядом. При определении порядка следования задач использован принцип «от простого к сложному». Такое представление материала облегчает преподавателю выбор тех задач, которые целесообразно решить в аудитории на практических занятиях, и тех, которые могут быть оставлены для индивидуальной и самостоятельной работы студентов.

Особое внимание уделено подборке задач по темам: случайные величины, случайные векторы, функции от случайных величин и векторов, центральная предельная теорема, поскольку они играют важную роль при дальнейшем изучении вероятностных дисциплин, таких как математическая статистика, теория случайных процессов, планирование эксперимента и статистический анализ.

Некоторые из предложенных задач носят теоретический характер и их решение основано на использовании непростых аналитических методов. Такие задачи рекомендуется обсуждать на индивидуальных занятиях. С другой стороны, их включение в сборник усиливает тот теоретический справочный материал, которым можно воспользоваться при изучении ряда дисциплин магистерских программ, что способствует обеспечению преемственности и непрерывности подготовки по направлению «Прикладная математика и информатика» в области вероятностно-статистических методов.

Практически ко всем задачам приведены ответы, а к части задач – решения или указания по их решению.

В конце сборника приведены таблицы некоторых распределений, список рекомендуемой литературы и предметный указатель. Список литературы охватывает общедоступные задачники и использованные теоретические курсы. Предметный указатель отчасти выполняет функции путеводителя по основным встречающимся понятиям. В нем для каждого из ключевых понятий приводится не только номер страницы, где это понятие появляется впервые, но и номера страниц и номера задач, где оно существенно используется. За счет этого можно проследить, каким образом то или иное понятие (например, нормальный закон распределения) приобретает дополнительную смысловую нагрузку по мере изучения курса.

1. Случайные события

1.1. Случайный эксперимент, случайные события и операции над ними

В теории вероятностей рассматриваются случайные (стохастические) эксперименты, которые могут быть повторены сколько угодно раз в одних и тех же условиях, но результаты которых не могут быть наперед предсказаны.

Множество всех возможных, взаимоисключающих исходов случайного эксперимента называется пространством элементарных событий . При этом элементы множества называются элементарными событиями (элементарными исходами) и обозначаются (с индексом или без).

Случайными событиями называются подмножества пространства элементарных событий . Говорят, что в результате случайного эксперимента произошло событие , если в эксперименте произошел один из элементарных исходов, входящих в множество.

Событие называется достоверным, оно всегда происходит в результате эксперимента. Невозможным называется событие , которое никогда не может произойти в результате эксперимента.

Суммой событий иназывается событие (или ), состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий или. Событиепроисходит тогда и только тогда, когда происходит или событиеА, или событие В, или оба этих события одновременно.

Произведением событий иназывается событие (или ), состоящее из всех элементарных исходов, принадлежащих и событию А, и событию В. Событие происходит тогда и только тогда, когда событияА и В происходят одновременно.

Разностью событий иназывается событие (или ), состоящее из всех элементарных исходов, принадлежащих событию А, но не принадлежащих событию В. Событие происходит тогда и только тогда, когда происходит событиеА, но не происходит событие В.

Противоположным событию называется событие, состоящее из всех элементарных исходов, не принадлежащих событиюА. Событие происходит тогда и только тогда, когда событиеА не происходит. Очевидно, что

Симметрической разностью событий и называется событие

.

Говорят, что событие влечет событие (или событиеследует из события ) и обозначают , если все элементарные события, принадлежащие событиюА, принадлежат также и событию В. Если , то всегда, как только происходит событие, происходит и событие.

Говорят, что события А и В являются равносильными и обозначают А=В, если и одновременно.

События иназываютсянесовместными, если они не могут произойти одновременно, то есть .

Графическая иллюстрация операций над событиями представлена на рис. 1.1.

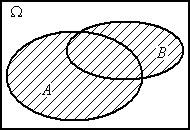
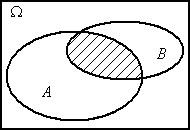
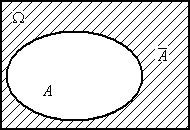
A+B AB

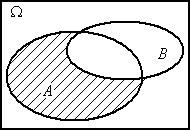
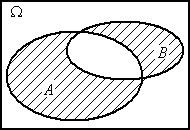
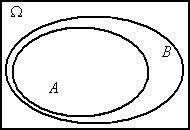
A–B

Рис. 1.1. Операции над событиями (результат – заштрихованная область)

Упростить выражения, содержащие события, часто позволяют, так называемые, соотношения дополнительности («законы де Моргана»):

;.

Полной группой событий называется совокупность событий , удовлетворяющих условиям:

1) события являются попарно несовместными:

для всех ;

2) сумма всех событий есть событие достоверное:

.

Пример 1. Эксперимент состоит в случайном выборе трех приборов из партии, содержащей годные и бракованные приборы. Описать пространство элементарных событий и события: = {хотя бы один из трех выбранных приборов бракованный},= {все приборы годные}. Что означают событияи?

Решение. Для описания пространства элементарных событий необходимо указать, что является элементарным исходом случайного экспериментаи перечислить все возможные взаимоисключающие исходы (события). В нашем случае каждый из трех выбранных приборов может быть годным (Г) или бракованным (Б). Поэтому элементарным исходом является любая тройка, составленная из символовГ и Б, и пространство элементарных событий имеет вид:

{БББ, ББГ, БГБ, ГББ, БГГ, ГБГ, ГГБ, ГГГ}.

Для описания события А необходимо явно указать те элементарные события , которые принадлежат событиюА. В нашем случае:

{хотя бы один из трех приборов бракованный}=

={БББ, ББГ, БГБ, ГББ, БГГ, ГБГ, ГГБ}.

Аналогично для события В имеем:

{все приборы годные}={ГГГ}.

Нетрудно видеть, что в данном случае сумма событий А и В есть событие достоверное: ; является противоположным событию :;– событиеневозможное. Следовательно, события А и являютсянесовместными, и, более того, образуют полную группу событий.

Замечание: Заметим, что элементарные исходы, а, следовательно, пространство элементарных событий и любое случайное событие, можно задать различными способами: формулой, текстом на естественном языке развернуто или кратко, графически. Так, например, в условиях предыдущего примера можно было бы вместо символов Г и Б использовать соответственно числа 1 и 0. Тогда элементарным исходом эксперимента являлось бы трехзначное двоичное число.

Отметим также, что в одном и том же случайном эксперименте возможна различная интерпретация элементарных исходов.

Пример 2. Схема электрической цепи изображена на рисунке 1.2. Рассматриваются следующие события: {вышел из строя элемент },{вышел из строя элемент }, (). Записать выражения для событий{разрыв цепи} и .

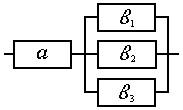
Рис. 1.2.

Решение. Разрыв цепи произойдет в том случае, если выйдет из строя или элемент , или все элементы(). Поскольку эти события соответственно равныи, то.

Используя соотношения дополнительности («законы де Моргана»), находим:

.

Задачи

1.1.1. Эксперимент состоит в однократном бросании двух игральных костей. Пусть событие состоит в том, что сумма выпавших очков чётная, а событие заключается в том, что выпала хотя бы одна единица. Описать пространство элементарных событий и события , ,.

1.1.2. Описать пространство элементарных исходов, соответствующее трём независимым испытаниям, в каждом из которых может наступить успех У или неуспех (неудача) Н. Выразить через элементарные исходы следующие события:

а) {в первом испытании наступил успех};

б) {наступило ровно два успеха};

в) {наступило не больше двух успехов}.

1.1.3. Игральная кость подбрасывается дважды. Описать пространство элементарных событий и события:

{сумма очков равна 10};

{по крайней мере, один раз появится 6 очков}.

1.1.4. Являются ли несовместными следующие события:

а) эксперимент – бросание одной монеты; события: {выпадение герба}, {выпадение цифры};

б) эксперимент – бросание двух монет; события: {выпадение герба на первой монете}, {выпадение цифры на второй монете};

в) эксперимент – два выстрела по мишени; события: {ни одного попадания}, {одно попадание}, {два попадания};

г) эксперимент – два выстрела по мишени; события: {хотя бы одно попадание}, {хотя бы один промах};

д) эксперимент – вынимание двух карт из колоды; события: {появление двух черных карт}, {появление туза}, {появление дамы}?

1.1.5. Эксперимент состоит в бросании двух монет. Рассматриваются следующие события:

{появление герба на первой монете};

{появление цифры на первой монете};

{появление герба на второй монете};

{появление цифры на второй монете};

{появление хотя бы одного герба};

{появление хотя бы одной цифры};

{появление одного герба и одной цифры};

{не появление ни одного герба};

{появление двух гербов}.

Определить, каким событиям этого списка равносильны следующие события: 1) ; 2); 3); 4); 5) ; 6) ; 7) .

1.1.6. Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события:

{обнаружен ровно один из четырех объектов};

{обнаружен хотя бы один объект};

{обнаружено не менее двух объектов};

{обнаружено ровно два объекта};

{обнаружено ровно три объекта};

{обнаружены все четыре объекта}.

Указать, в чем состоят события: 1) ; 2); 3); 4); 5) ; 6) .

Равносильны ли события Равносильны ли события

1.1.7. Назвать противоположные для следующих событий:

{выпадение двух гербов при бросании двух монет};

{появление белого шара при вынимании одного шара из урны, в которой 2 белых, 3 черных и 4 красных шара};

{три попадания при трех выстрелах};

{хотя бы одно попадание при пяти выстрелах};

{не более двух попаданий при пяти выстрелах};

{выигрыш первого игрока при игре в шахматы}.

1.1.8. Среди студентов, занимающихся спортом, выбирают наудачу одного. Пусть событие заключается в том, что выбранный студент окажется юношей. Событие – в том, что он не курит, а событие – в том, что он живет в общежитии. а) Описать событие ; б) при каком условии будет иметь место равенство ? в) когда будет справедливо соотношение ? г) когда будет справедливо равенство, будет ли оно иметь место, если все юноши курят?

1.1.9. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями с радиусами , причем . Событие {попадание в круг радиуса }. Что означают события:

; ; ; ?

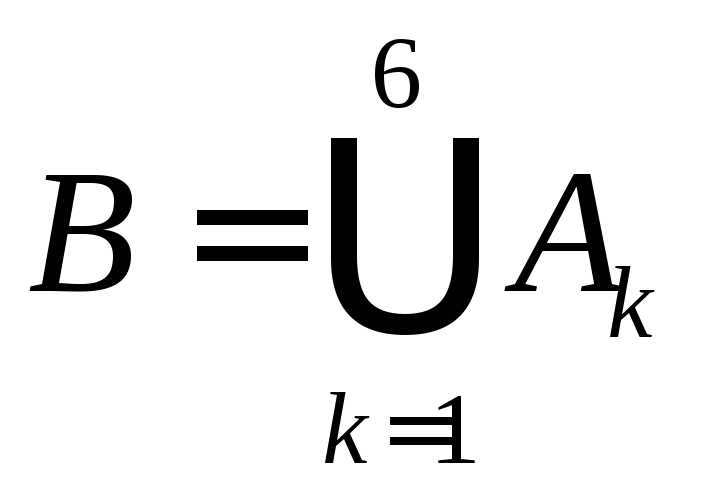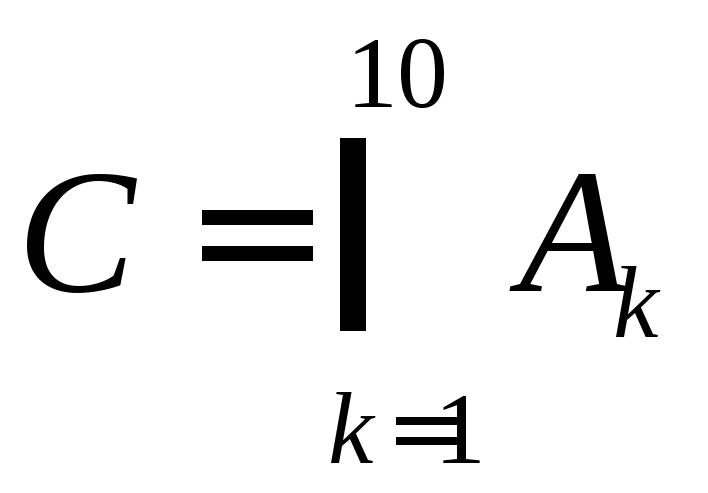1.1.10. Из таблицы случайных чисел наудачу взято одно число. Рассматриваются события: {выбранное число делится на 5}, {данное число оканчивается нулем}. Что означают события и ?

1.1.11. Из множества супружеских пар наугад выбирается одна пара. Рассматриваются события: {мужу больше 30 лет}; {муж старше жены}; {жене больше 30 лет}.

а) Выяснить смысл событий , , ;

б) проверить, что .

1.1.12. Образуют ли полную группу событий следующие события:

а) эксперимент – бросание монеты; события: {выпадение герба}; {выпадение цифры};

б) эксперимент – бросание двух монет; события: {выпадение двух гербов}; {выпадение двух цифр};

в) эксперимент – два выстрела по мишени; события: {ни одного попадания}; {одно попадание}; {два попадания};

г) эксперимент – два выстрела по мишени; события: {хотя бы одно попадание}; {хотя бы один промах};

д) эксперимент – вынимание карты из колоды; события: {появление карты пиковой масти}; {появление карты бубновой масти}; {появление карты крестовой масти}?

1.1.13. Два шахматиста играют одну партию. События: {выигрывает первый игрок}; {выигрывает второй игрок}. Какое событие следует добавить к указанной совокупности, чтобы получилась полная группа событий?

1.1.14. Пусть А и В – произвольные события. Доказать, что события ,иобразуют полную группу событий.

1.1.15. По мишени производится три выстрела. Рассматриваются события: {попадание при -ом выстреле}, (). Представить в виде сумм, произведений или сумм произведений событий иследующие события:

{все три попадания};

{все три промаха};

{хотя бы одно попадание};

{хотя бы один промах};

{не меньше двух попаданий};

{не больше одного попадания};

{попадание в мишень не раньше, чем при третьем выстреле}.

1.1.16. Пусть А, B, С - три произвольных события. Найти выражения для событий, состоящих в том, что из A, B, C произошли: а) только A; б) А и B, но не произошло; в) все три события; г) по крайней мере одно событие; д) одно и только одно событие; е) не произошло ни одного события; ж) не более двух событий.

1.1.17. Прибор состоит из двух блоков первого типа и трех блоков второго типа. Рассматриваются события:{исправен k-й блок первого типа}, ,{исправен j-й блок второго типа}, . Прибор работоспособен, если исправны хотя бы одинблок первого типа и не менее двух блоков второго типа. Выразить событие , означающее работоспособность прибора, через A_k и B_j.

1.1.18. Рабочий изготовил n – деталей. События: {i-ая деталь имеет дефект}, . Выразить через следующие события:

а) ни одна из деталей не имеет дефектов;

б) хотя бы одна деталь имеет дефект;

в) только одна деталь имеет дефект;

г) не более двух деталей имеют дефект;

д) по крайней мере, две детали не имеют дефектов;

е) две детали дефектны.

1.1.19. Пусть . Упростить выражения:

а) ; б) ; в) ; г) .

1.1.20. Пусть A, B, C - случайные события. Выяснить смысл равенств:

а) ; б).

1.1.21. Когда возможны равенства:

а) ; б) ; в) ?

1.1.22. Доказать, что следующие события достоверны:

а) ; б) .

1.1.23. Доказать, что событие невозможно.

1.1.24. Найти простые выражения для событий:

а) ; б) ; в).

1.1.25. Обязаны ли быть равносильными события А и B, если: а) ; б) ( - некоторое событие); в) ( - некоторое событие); г) ; д) ; е); ж) ?

1.1.26. Сумма двух событий может быть выражена как сумма двух несовместных событий: . Выразить аналогичным образом сумму трех событий A, B, и C.

1.1.27. Установить, какие из следующих соотношений справедливы:

а) ; б) ; в);

г) ; д).

1.1.28. Найти событие X из равенства .

1.1.29. Показать, что равенство имеет место тогда и только тогда, когда .

1.1.30. Функцию

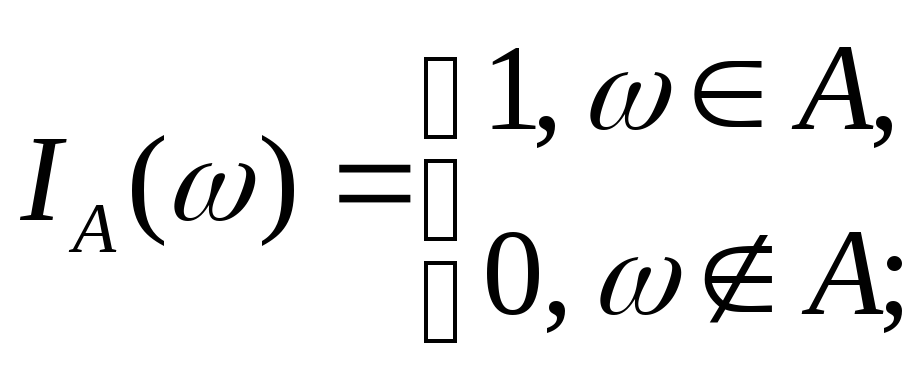
называют индикатором события A. Доказать, что:

а) ; б) ;

в) ; г) .