
- •Ответы и указания
- •1. Случайные события
- •1.1. Случайный эксперимент, случайные события и операции над ними
- •1.2. Классическое определение вероятности
- •1.3. Геометрическое определение вероятности
- •1.4. Аксиомы теории вероятностей. Условная вероятность. Независимость случайных событий.
- •1.5. Формула полной вероятности и формула Байеса
- •1.6 Схема Бернулли. Предельные теоремы в схеме Бернулли
- •2. Случайные величины и случайные векторы
- •2.1. Случайные величины. Законы распределения и числовые характеристики
- •Дискретные случайные величины
- •Непрерывные случайные величины
- •Основные законы распределения случайных величин
- •2.2. Случайные векторы. Законы распределения и числовые характеристики. Условные законы распределения. Независимость случайных величин.
- •Дискретные случайные векторы
- •Непрерывные случайные векторы
- •2.3. Функции от случайных величин и векторов Законы распределения функций от случайных величин
- •3. Законы больших чисел и предельные теоремы теории вероятностей
- •3.1. Неравенство Чебышева и законы больших чисел
- •3.2. Производящие и характеристические функции
- •3.3. Предельные теоремы теории вероятностей
- •Список литературы Учебники и учебные пособия
- •Сборники задач
Ответы и указания
1. Случайные события
1.1. Случайный эксперимент, случайные события и операции над ними
1.1.1.![]() ,где
,где![]() -число очков на
первой и второй костях соответственно;
-число очков на
первой и второй костях соответственно;
![]() ;
;![]() .
.
1.1.2.
={УУУ,
УУН,
УНУ,
НУУ,
УНН,
НУН,
ННУ,
ННН};
A={УУУ,
УУН,УНУ,
УНН};
B={УУН,
УНУ,
НУУ};
C={УУН,
УНУ,
НУУ,
УНН,
НУН,
ННУ,
ННН}
=
![]() .
.
1.1.3.![]() ,где
,где![]() -число очков на
первой и второй костях соответственно;
-число очков на
первой и второй костях соответственно;
![]() .
.
1.1.4. а) да; б) нет; в) да; г) нет; д) нет.
1.1.5.![]()
![]()
1.1.6.
![]()
![]()
1.1.7.
![]()
![]()
![]()
![]()
![]()
![]()
1.1.8. а) Выбран юноша, который не живет в общежитии и не курит; б) когда все юноши живут в общежитии и не курят; в) когда курящие живут только в общежитии; г) когда ни одна девушка не курит, а все юноши курят. Нет, так как могут курить и девушки.
1.1.9.
B=A6;
C=A1;
D=A5;
E={(x,y):
r1![]() r2}.
r2}.
1.1.10. Выбранное число оканчивается цифрой 5.
1.1.11.
а)
![]() - оба супруга старше 30 лет, причем муж
старше жены;
- оба супруга старше 30 лет, причем муж
старше жены;
![]() ,
т.е. мужу больше 30 лет, но он не старше
своей жены;
,
т.е. мужу больше 30 лет, но он не старше
своей жены;
![]() - оба супруга старше 30 лет, причем муж
не старше своей жены;
- оба супруга старше 30 лет, причем муж
не старше своей жены;
б)
![]() - мужу больше 30 лет, а жене не больше 30
лет, следовательно, муж старше жены,
т.е.
- мужу больше 30 лет, а жене не больше 30
лет, следовательно, муж старше жены,
т.е.![]()
![]()
1.1.12. а) да; б) нет; в) да; г) нет; д) нет.
1.1.13.
![]()
1.1.14.
![]()
![]()
![]()
![]()
т.е. события образуют полную группу событий.
1.1.15.
![]()
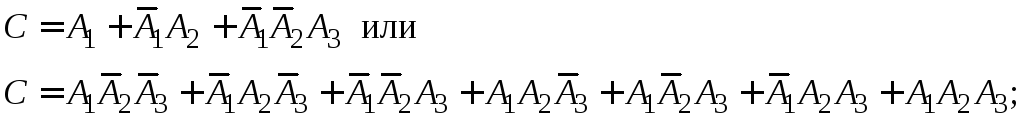
![]()
![]()
1.1.16.
а)
A![]() ;
б)
AB
;
б)
AB![]() ;в)
ABC;
г)
A+B+C;
д)
A
;в)
ABC;
г)
A+B+C;
д)
A![]() +
+![]() B
B![]() +
+![]() C;
е)
C;
е)![]() ;ж)
(A+B+C)-ABC.
;ж)
(A+B+C)-ABC.
1.1.17. C = (A1+A2)(B1B2+B1B3+B2B3).
1.1.18.
а)
![]() б)
б)
![]() в)
в)![]() г)
г)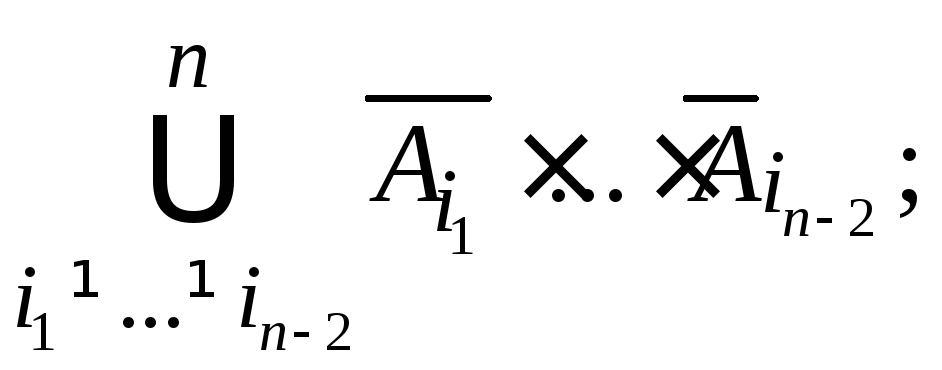
д)
![]() е)
е)![]()
1.1.19.
![]()
1.1.20. См. задачу 1.1.19.
1.1.21. а) A=, B=; б) A=, B=; в) A=B.
1.1.22.
а)
![]()
![]()
б)
![]()
![]()
1.1.23.
![]()
![]()
1.1.24. а) A; б) AB; в) B+AC.
1.1.25. В случаях а), г), д), ж) – да, в остальных нет.
1.1.26.
![]()
1.1.27. а), в), г), д) – не справедливы; б) – справедливо.
1.1.28.
X=![]() .
.
1.1.29.
1. Покажем,
что (![]() )C=
)C=![]() C+
C+![]() CAC=BC.
Переходя к противоположным событиям в
обеих частях соотношения, имеем:
(A+B)+
CAC=BC.
Переходя к противоположным событиям в
обеих частях соотношения, имеем:
(A+B)+![]() =(A+
=(A+![]() )(B+
)(B+![]() )(A+B)+
)(A+B)+![]() =AB+A
=AB+A![]() +B
+B![]() +
+![]()
A+B=AB+(A+B)
![]()
(A+B)C=ABCAC+BC=AC·BCAC=BC.
(A+B)C=ABCAC+BC=AC·BCAC=BC.
2.
Покажем, что AC=BC(![]() )C
=
)C
=![]() C+
C+![]() C.
C.
(![]() )C=(
-
(A+B))C=C
-
(AC+BC)=C
-
AC;
)C=(
-
(A+B))C=C
-
(AC+BC)=C
-
AC;
![]()
Следовательно,
(![]() )C==
)C==![]() C+
C+![]() C.
C.
1.2. Классическое определение вероятности
1.2.1. 1) да; 2) а) да; б) да; в) да; 3) нет; 4) нет; 5) а) нет; б) да; в) нет; 6) нет.
1.2.3. 0.096.
1.2.4. 5/9.
1.2.5.1/60.
1.2.6.![]()
![]() .
.
1.2.7.
а)
![]() б)
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)![]() ;
д)
;
д)![]() .
.
1.2.8.
![]() .
.
1.2.9. 1/9.
1.2.10.
а)
![]() ,
,![]() ;
б)
;
б)![]() .
.
1.2.11.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
1.2.12.
![]() .
.
1.2.13.1/2.
1.2.14.
![]() ;
;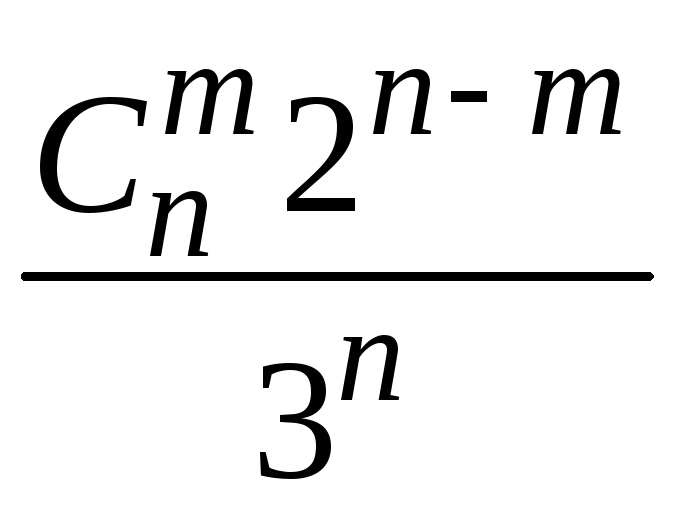
![]()
1.2.15. Из меньшего числа партий.
1.2.16.
а)
![]() ;
б)
;
б)![]() .
.
1.2.17.
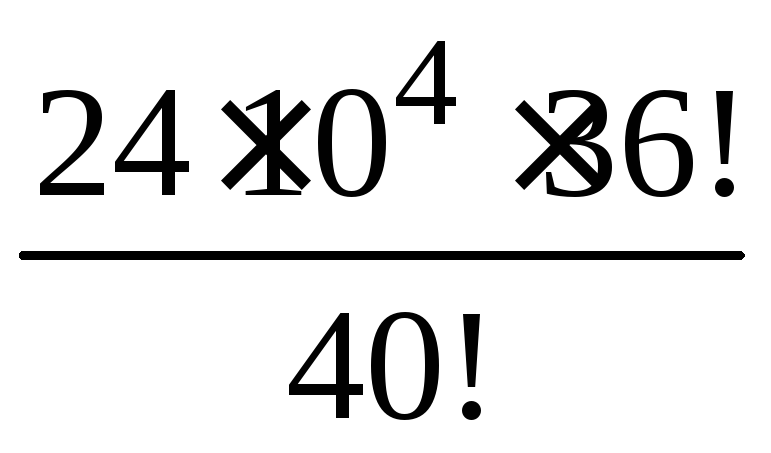 .
.
1.2.18.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
1.2.19.
![]() .
.
1.2.20. 2/5.
1.2.21.
![]() .
.
1.2.22. Указание. Лишь последняя цифра влияет на последнюю цифру квадрата и четвертой степени числа, а на последнюю цифру произведения чисел - их последние цифры. Поэтому можно рассматривать только однозначные числа. а) 0,2; б) 0,4; в) 0,04.
1.2.23.
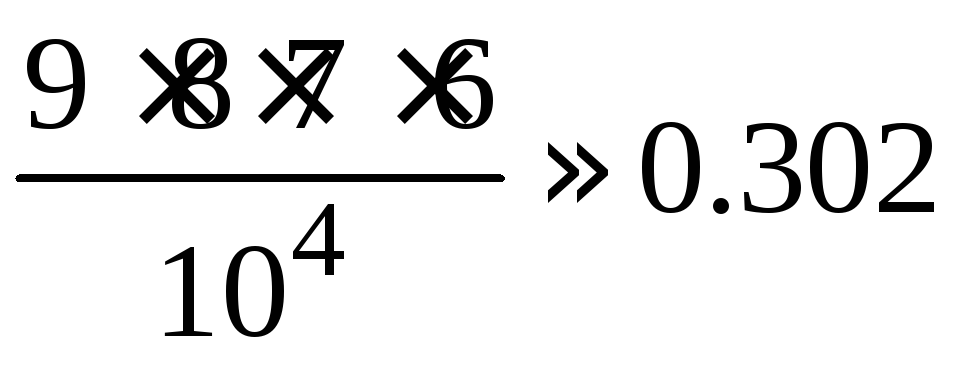 .
.
1.2.24.
![]() .
.
1.2.25.
![]() .
.
1.2.26.
![]() ;
;![]() .
.
1.2.27.
![]() ;
;
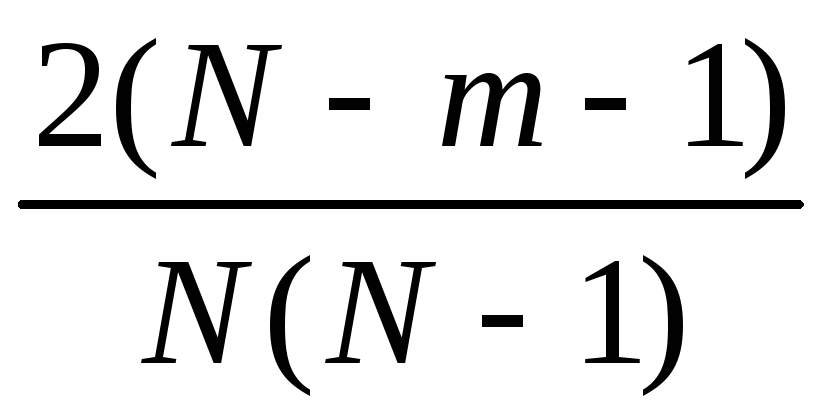 .
.
1.2.28. 1/126.
1.2.29.
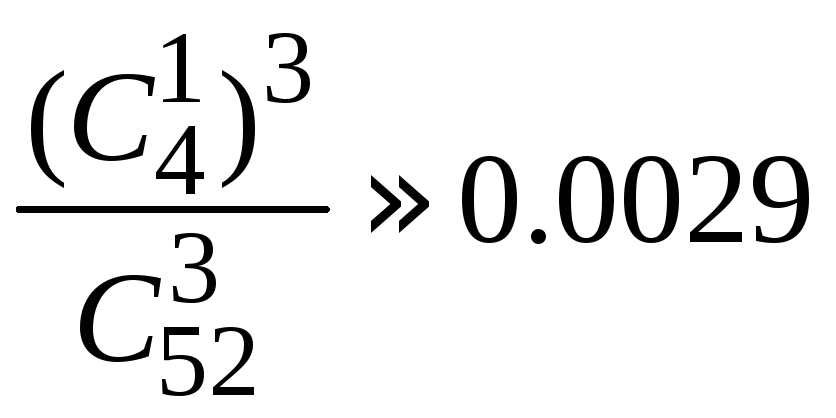 .
.
1.2.30.
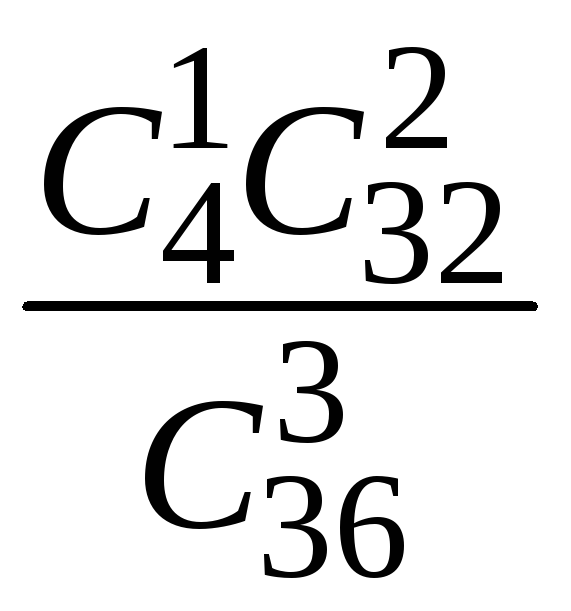 .
.
1.2.31.
![]()
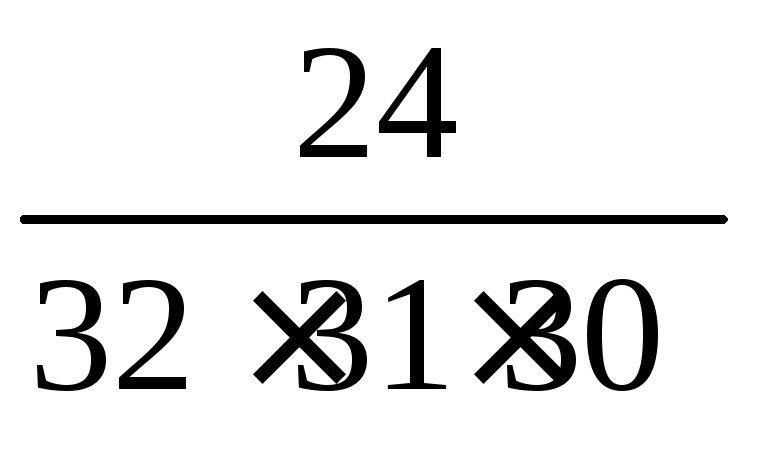 .
.
1.2.32.
![]()
1.2.33. 1/4.
1.2.34.
а)
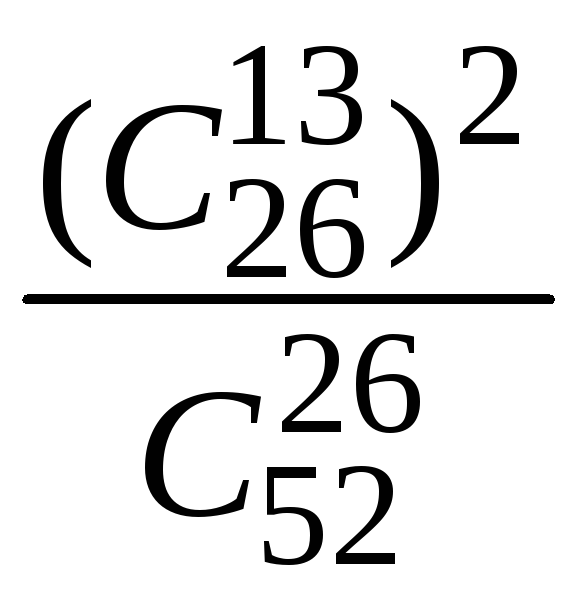 ;
б)
;
б)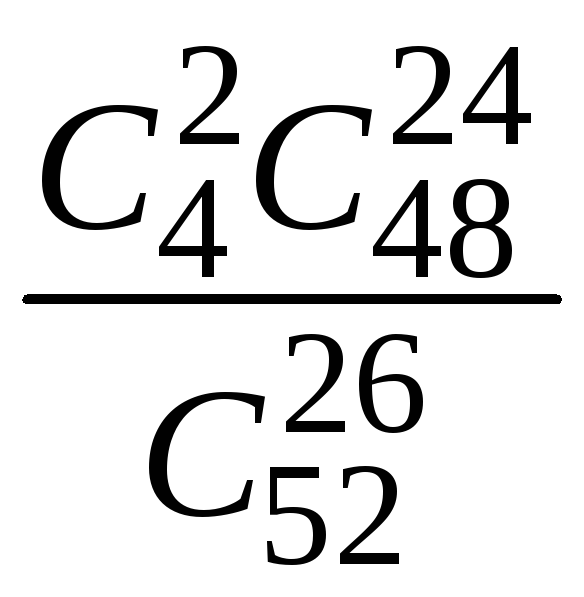 .
.
1.2.35.
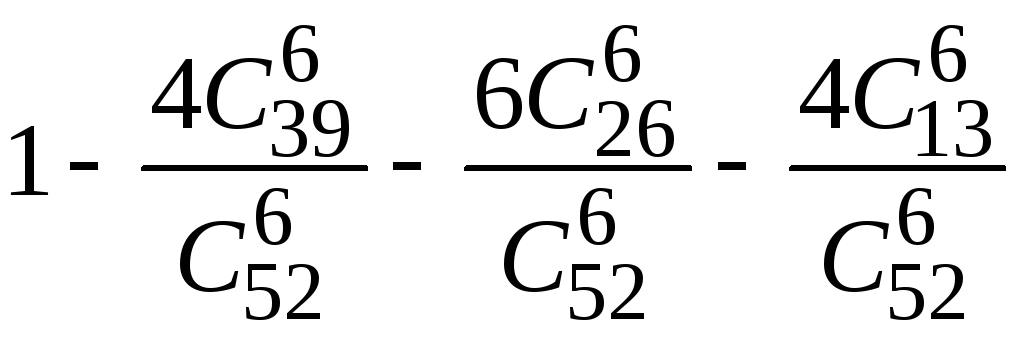 .
.
1.2.36. 9/28.
1.2.37. 2 красных шара и 1 синий.
1.2.38.
а)
![]() ;
б)
;
б)![]() .
.
1.2.39.
![]() .
.
1.2.40.
![]() .
.
1.2.41.
![]()
1.2.42.
![]()
1.2.43.
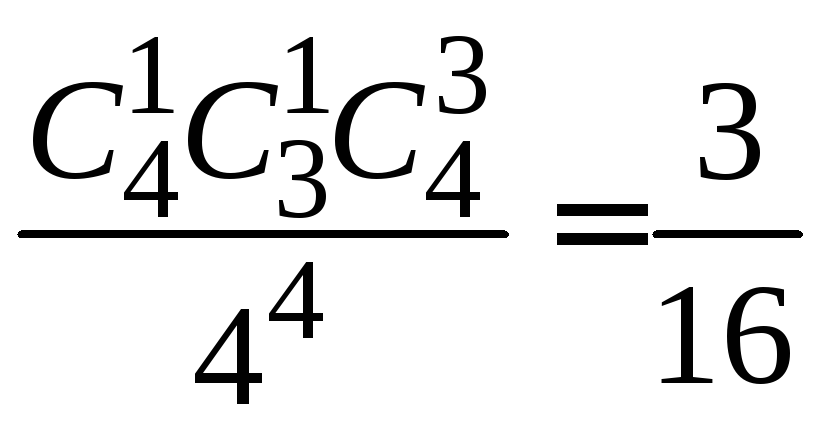 .
.
1.2.44.
![]() .
.
1.2.45.
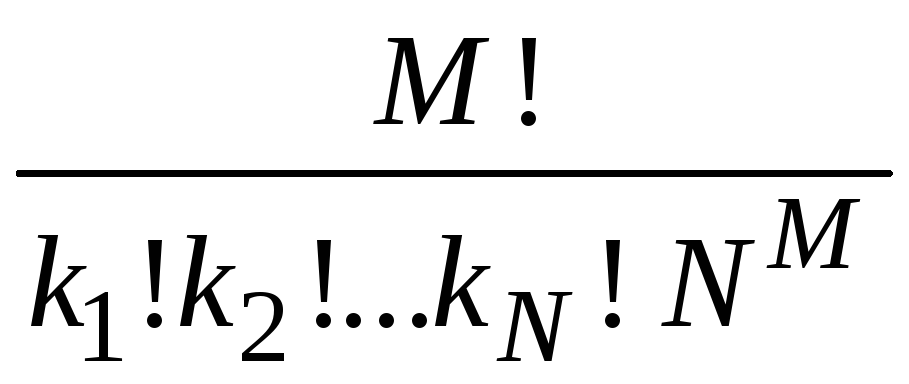 .
.
1.2.46.
![]()
1.2.47.
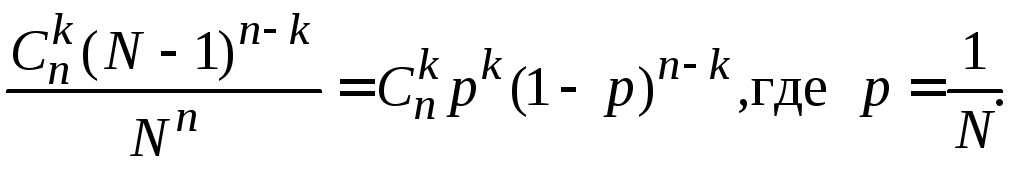 .
.
1.2.49.
![]() .
.
1.2.50.
а)
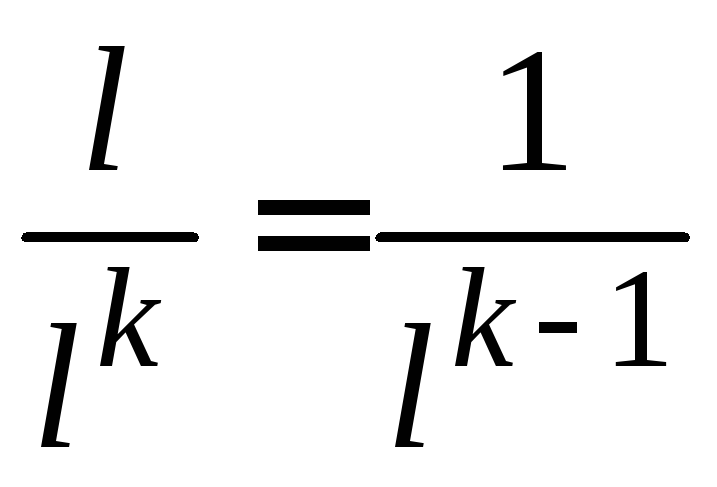 ;
б)
;
б)
![]() .
.
1.2.51.
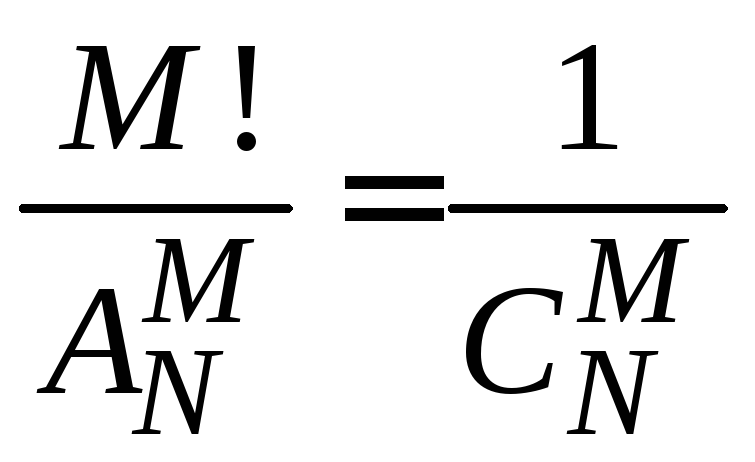 .
.
1.2.52.
а)
![]() б)
б)![]()
1.2.53. 0.055.
1.2.54.
![]()
1.2.55.
![]()
1.2.56.
а)
![]() б)
б)![]()
1.3. Геометрическое определение вероятности
1.3.1. 2/3.
1.3.2. 1/3 + 2/9ln2.
1.3.3. (1+ln4)/4.
1.3.4.
![]() .
.
1.3.5.
![]() .
.
1.3.6.
![]() .
.
1.3.7. 1/2.
1.3.8. 3/4.
1.3.9. а)2/3; б)1/12.
1.3.10. 9/13.
1.3.11.а)
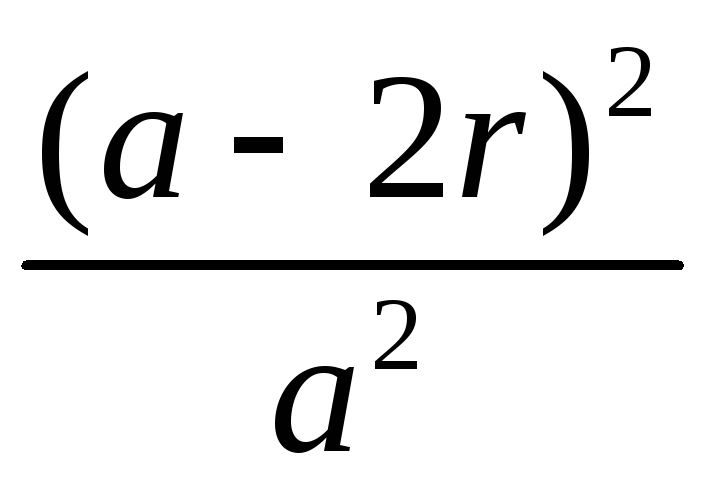 ;
б)
;
б)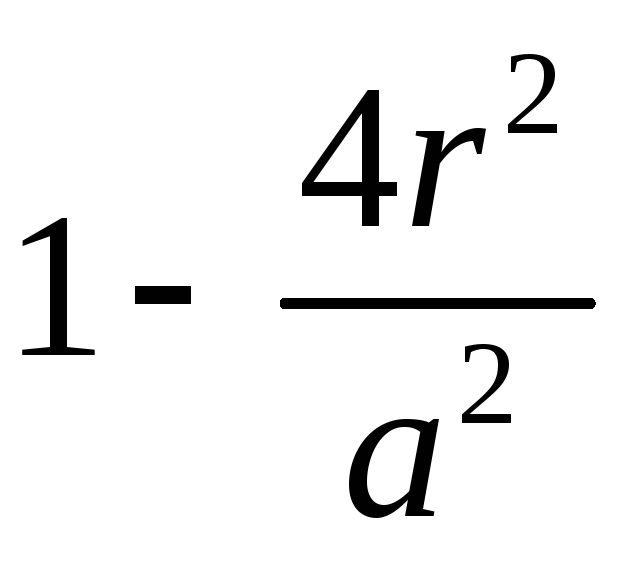 .
.
1.3.13.
![]() .
.
1.3.14.1/2.
1.3.15.![]() .
.
1.3.16. 5/6.
1.3.17. 1/4.
1.3.18.
![]()
1.3.19.
![]() .
.
1.3.20. 7/9.
1.3.21. 139/1152.
1.3.22.![]() .
.
1.3.23.
![]() .
.
1.3.24.
а)
![]() ;
б)
;
б)![]() .
.
1.3.25.
а)
![]() ;
б)
;
б)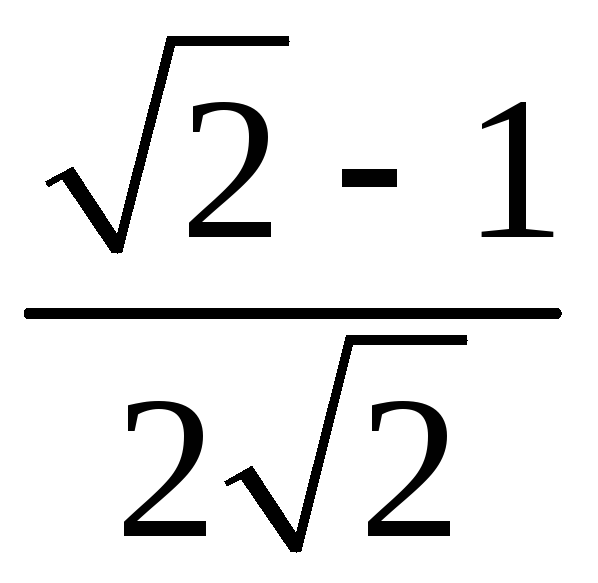 .
.
1.3.26.
![]() .
.
