3. Законы больших чисел и предельные теоремы теории вероятностей

3.1. Неравенство Чебышева и законы больших чисел

Если неотрицательная случайная величина имеет конечное математическое ожидание, то для любогосправедливо неравенство:

.

Если случайная величина имеет конечную дисперсию, то для любогосправедливы следующие неравенства (неравенства Чебышева):

;

.

Говорят, что последовательность случайных величин сходится по вероятности к величине (случайной или нет), если для любого

или, что эквивалентно,

Краткое обозначение сходимости по вероятности: при.

Говорят, что последовательность случайных величин имеющих конечные математические ожиданияподчиняется закону больших чисел, если

,

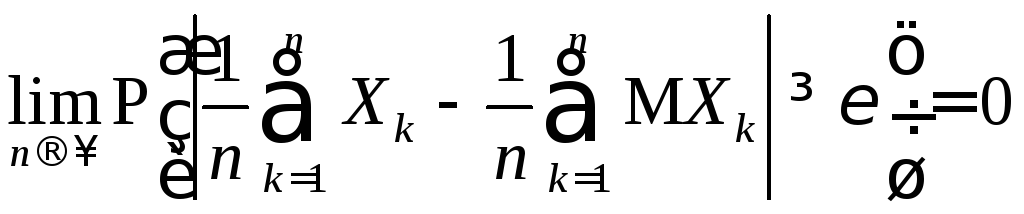или кратко,

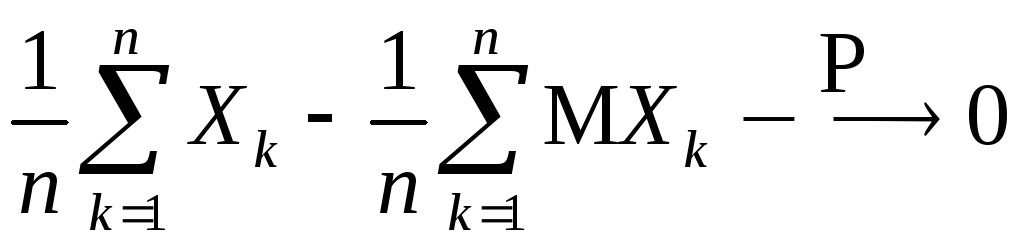при .

В частности, если все случайные величины в последовательности имеют одинаковые математические ожидания, то закон больших чисел записывается в виде:

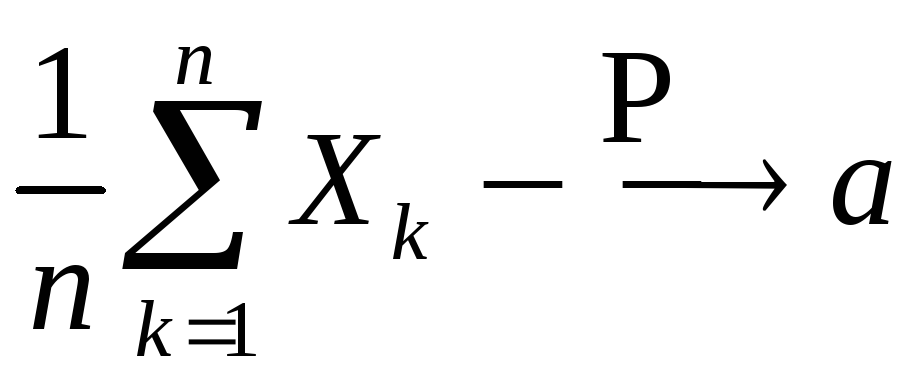при .

Теорема Хинчина (закон больших чисел для независимых, одинаково распределенных случайных величин).

Если случайные величины в последовательности являются независимыми, одинаково распределенными и имеют конечные математические ожиданиято

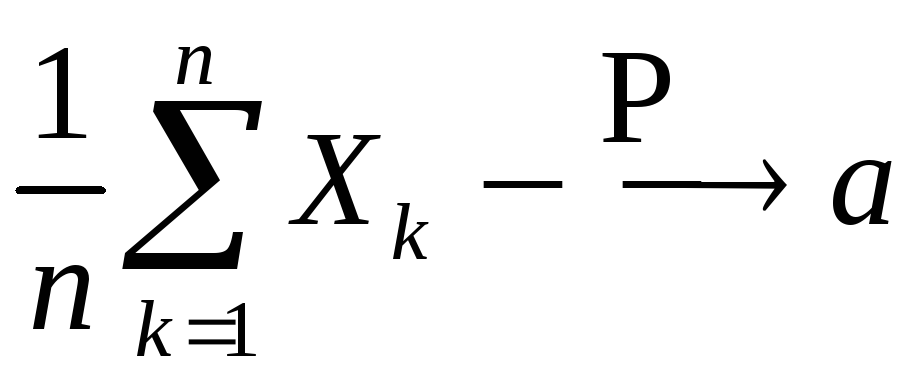при .

Теорема Чебышева (закон больших чисел для независимых, разнораспределенных случайных величин).

Если случайные величины в последовательности являются независимыми, а их дисперсииравномерно ограничены, то есть

то эта последовательность случайных величин подчиняется закону больших чисел.

Утверждение теоремы Чебышева остается справедливым и для попарно некоррелированных случайных величин , и, если вместо требования равномерной ограниченности дисперсий выполняется условие:

.

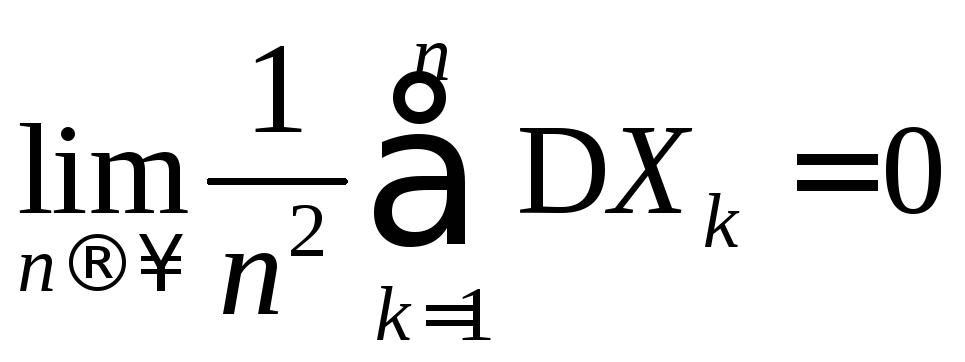Теорема Маркова (закон больших чисел для зависимых, разнораспределенных случайных величин).

Если дисперсии случайных величин в последовательности удовлетворяют условию

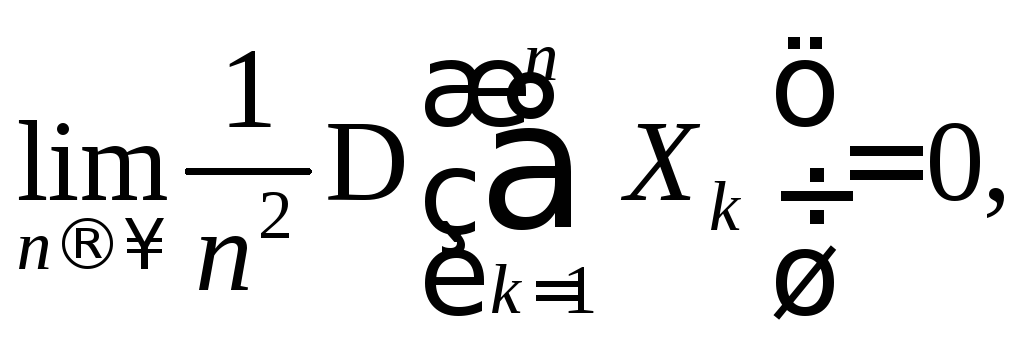
то эта последовательность случайных величин подчиняется закону больших чисел.

Теорема Бернулли.

Относительная частота появления событиявнезависимых испытаниях по схеме Бернулли сходится по вероятности прик вероятностинаступления событияв одном испытании, то есть для любого

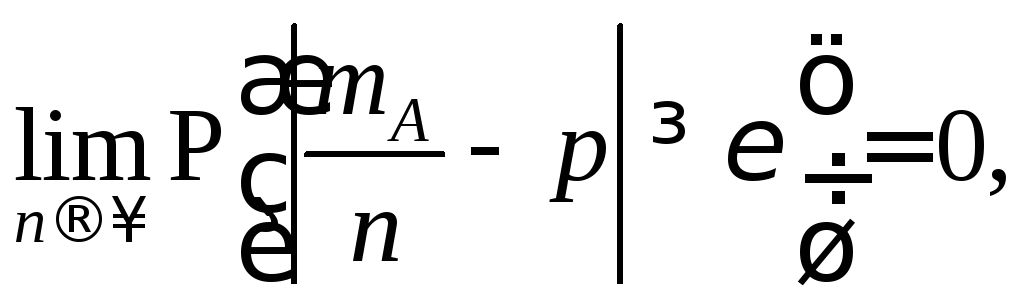
или, кратко

при .

Пример. Пусть - последовательность случайных величин, дисперсии которых ограничены одной и той же постоянной, а коэффициент корреляции любых случайных величини, не являющихся соседними в последовательности, равен нулю. Подчиняется ли эта последовательность случайных величин закону больших чисел?

Решение. Проверим выполнение условия в теореме Маркова:

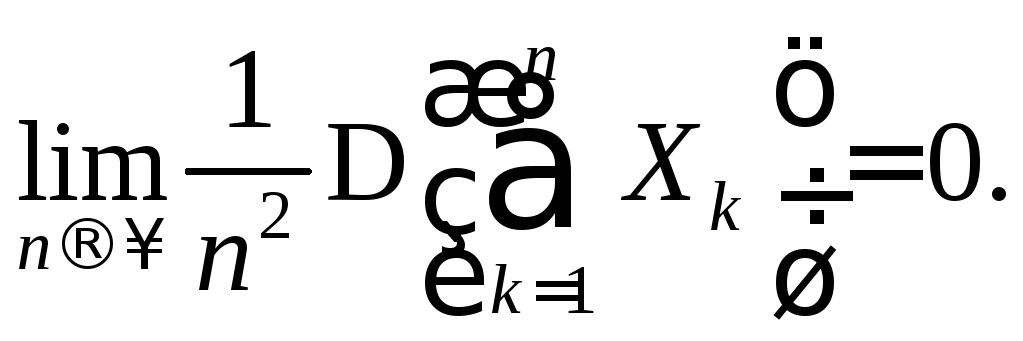
Из свойств дисперсии следует, что 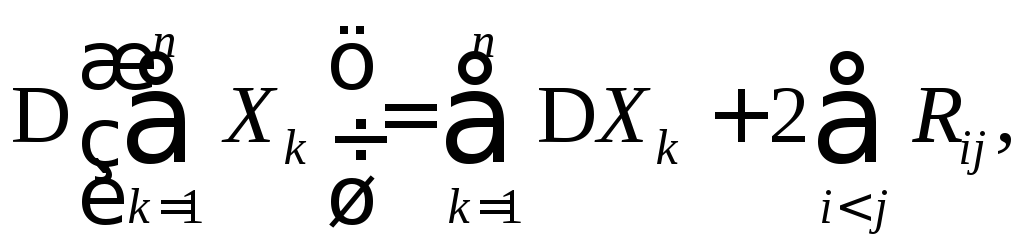где- корреляционный момент случайных величини. Но для, по условию,, если. Следовательно, в суммеравны нулю все слагаемые кроме, может быть,(их ровно).

Для любых и, так как, по условиюдля любого. Поэтому

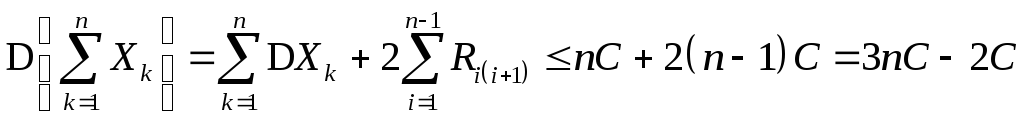
и получаем, что

.

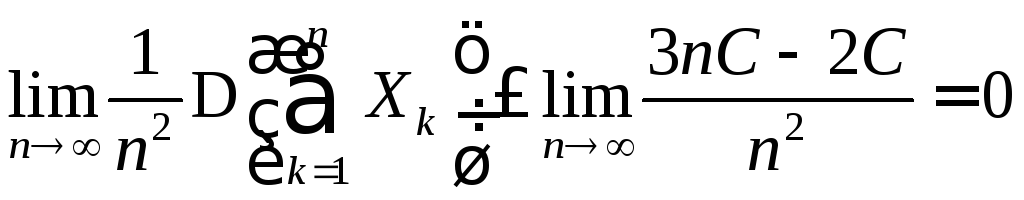Таким образом, последовательность случайных величин подчиняется закону больших чисел.

Задачи

3.1.1. Показать, что если существует MX², то

.

3.1.2. Дискретная случайная величина X имеет закон распределения:

X	0,3	0,6
	0,2	0,8

Используя неравенство Чебышева, оценить вероятность того, что .

3.1.3. Пусть С помощью неравенства Чебышева оценить вероятность того, что.

3.1.4. Среднее значение длины детали 50 см, а дисперсия 0,1см². Пользуясь неравенством Чебышева, оценить вероятность того, что случайно взятая деталь окажется по длине не меньше 49,5 см и не больше 50,5 см.

3.1.5. Длина изготовляемых изделий представляет случайную величину, среднее значение которой равно 90 см. Дисперсия этой величины равна 0,0225 см². Используя неравенство Чебышева, оценить вероятность того, что:

а) отклонение длины изготовленного изделия от ее среднего значения по абсолютной величине не превзойдет 0,4 см;

б) длина изделия выразится числом, заключенным между 89,7 см и 90,3 см.

3.1.6. Пользуясь неравенством Чебышева, оценить вероятность того, что случайная величина X отклонится от своего математического ожидания:

а) менее чем на три средних квадратических отклонения;

б) не менее чем на два средних квадратических отклонения.

3.1.7. иПользуясь неравенством Чебышева, найти.

3.1.8. Устройство состоит из десяти независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом отказов за время Т окажется меньше двух.

3.1.9. Пусть случайная величина Х имеет нормальное распределение N(a,). Оценить с помощью неравенства Чебышева .

Сравнить с точным значением этой вероятности.

3.1.10. За значение некоторой величины принимают среднее арифметическое достаточно большого числа ее измерений. Предполагая, что среднее квадратическое отклонение возможных результатов каждого измерения не превосходит 1 см, оценить вероятность того, что при 1000 измерениях отклонение принятого значения от истинного не превзойдёт по абсолютной величине 0,1 см.

3.1.11. Предполагается провести 10 измерений неизвестной величиныа. Считая измерения независимыми, нормально распределенными случайными величинами с,найти наименьшеетакое, чтобы выполнялось неравенство

.

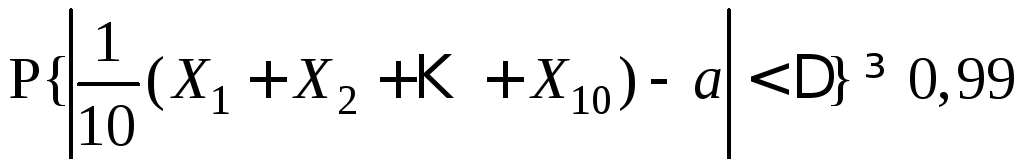Указание. Найти точное значение и сравнить с оценкой, полученной с помощью неравенства Чебышева.

3.1.12. Сколько нужно произвести испытаний, чтобы с вероятностью не менее 0,99 можно было утверждать, что отклонение относительной частоты от вероятности события, равной 0,35, будет не более 0,01?

3.1.13. Сколько следует произвести испытаний, чтобы вероятность выполнения неравенства 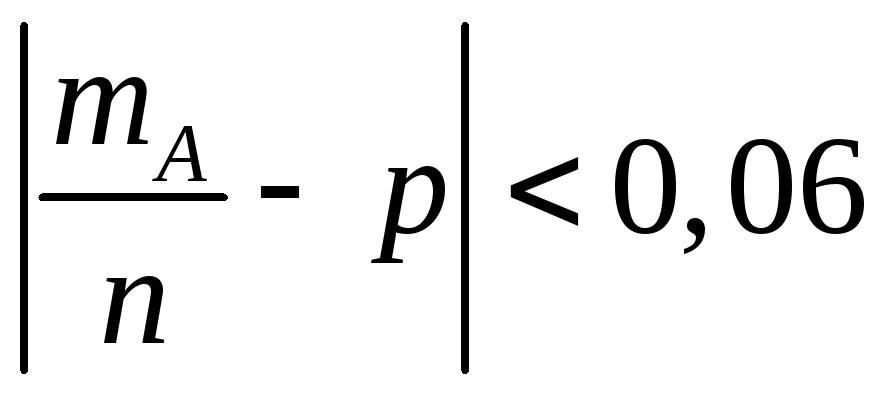для событияА превысила 0,79? Считать вероятность появления данного события в отдельном испытании равной 0,7.

3.1.14. Пусть случайная величина X такова, что существует (a>0 – постоянная). Доказать, что тогда

.

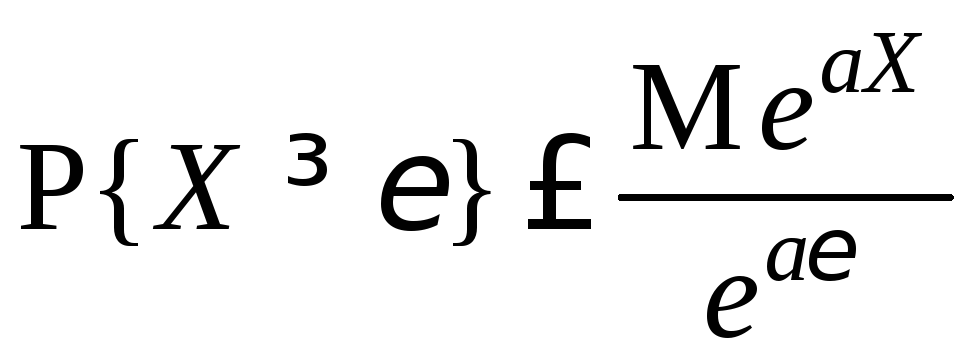3.1.15. Пусть - неотрицательная неубывающая функция. Доказать, что если существуетто

.

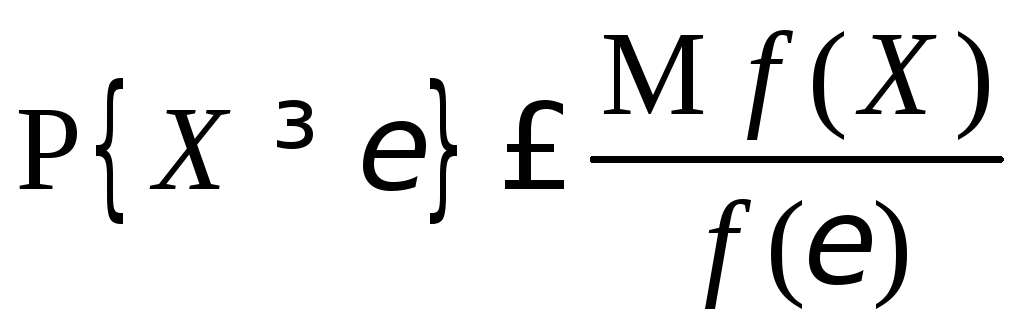3.1.16. Показать, что если существует ,, то справедливо неравенство:

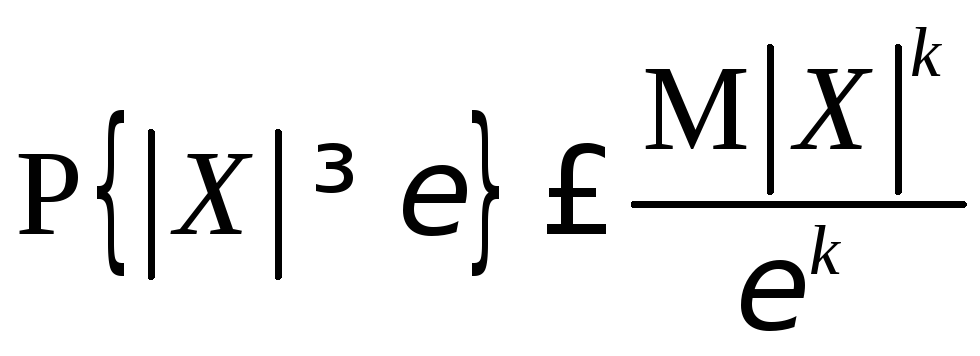(неравенство Маркова).

3.1.17. Допуская существование , доказать, что имеют место следующие оценки сверху и снизу для :

а) 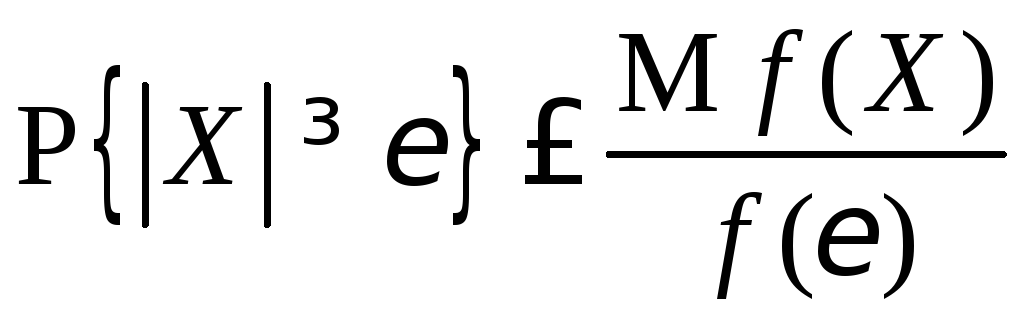, еслинеотрицательная, четная, неубывающая на интервалефункция;

б) , еслинеотрицательная, четная, неубывающая на интервале и ограниченная функция.

3.1.18. Дана последовательность независимых случайных величин Каждая случайная величина может принимать только три значения:, 0, с вероятностями, равными соответственно ,,. Применима ли к этой последовательности теорема Чебышева?

3.1.19. Дана последовательность независимых случайных величин Каждая случайная величина имеет закон распределения:

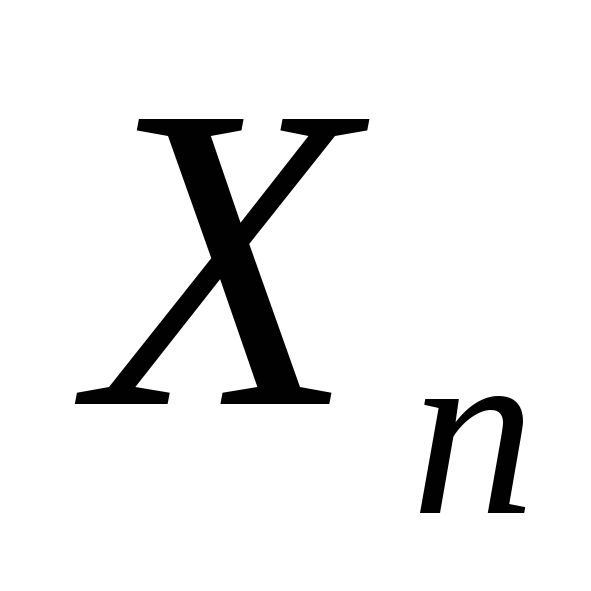
	-n	0	n
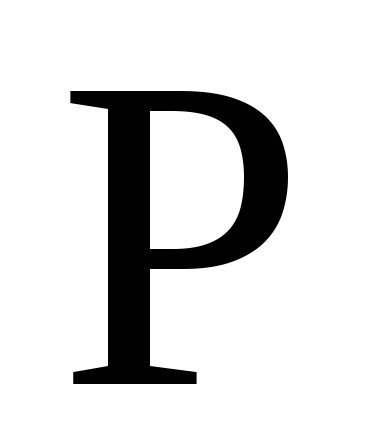
	1/2n2	1-1/n2	1/2n2

Применима ли к этой последовательности теорема Чебышева?

3.1.20. Дана последовательность независимых случайных величин в которой каждая из случайных величинХ_n имеет закон распределения:

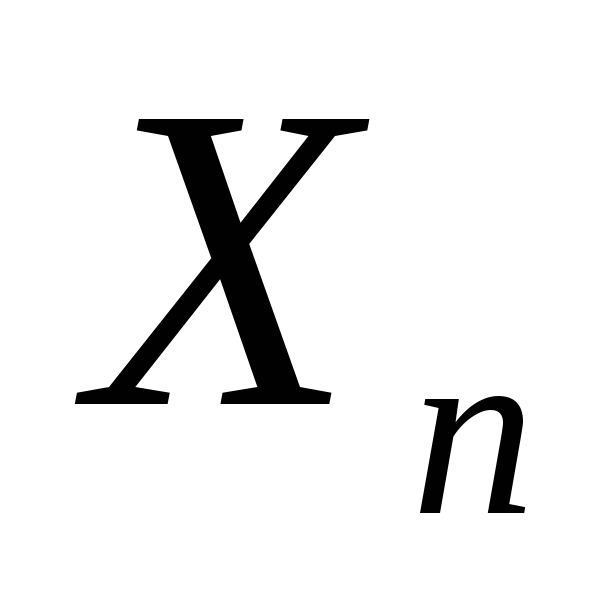
	-а	а
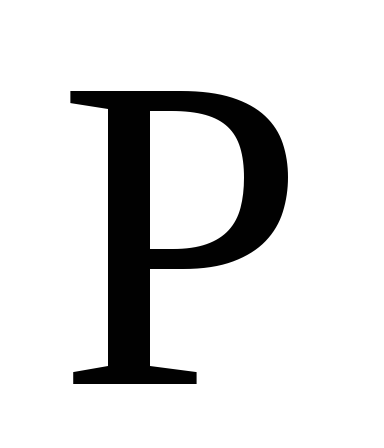
	(n+1)/(2n+1)	n/(2n+1)

Применима ли к этой последовательности теорема Чебышева?

3.1.21.. Каждая случайная величина X_n в последовательности независимых случайных величин может принимать только два значенияс вероятностями равными 1/2. Подчиняется ли эта последовательность случайных величин закону больших чисел?

3.1.22. Подчиняется ли закону больших чисел последовательность независимых случайных величин если каждая из случайных величинX_k имеет закон распределения:

?

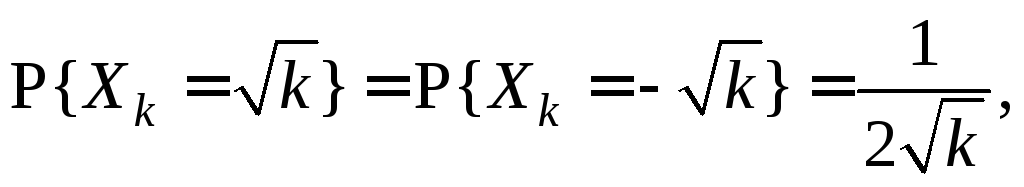
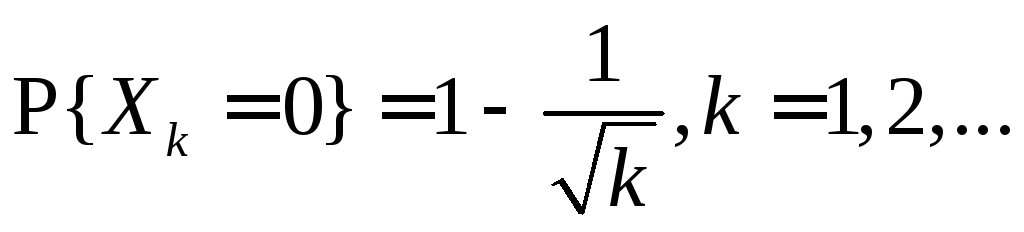3.1.23. Подчиняется ли закону больших чисел последовательность независимых случайных величин если каждая случайная величинапринимает значения,

причем

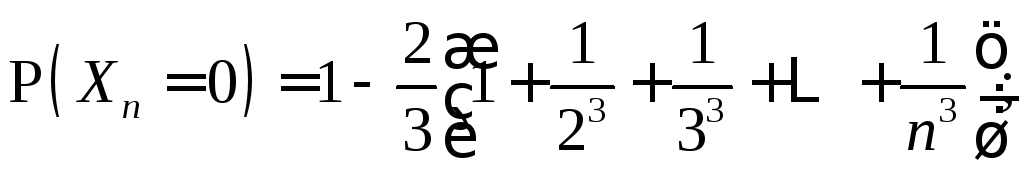
3.1.24. Подчиняется ли закону больших чисел последовательность независимых случайных величин если каждая из случайных величинX_k имеет закон распределения:

, , k1 ?

3.1.25. Случайные величины являются независимыми и распределены по закону равнобедренного треугольника (Симпсона) на отрезке, т.е. имеют плотности вероятностей вида:

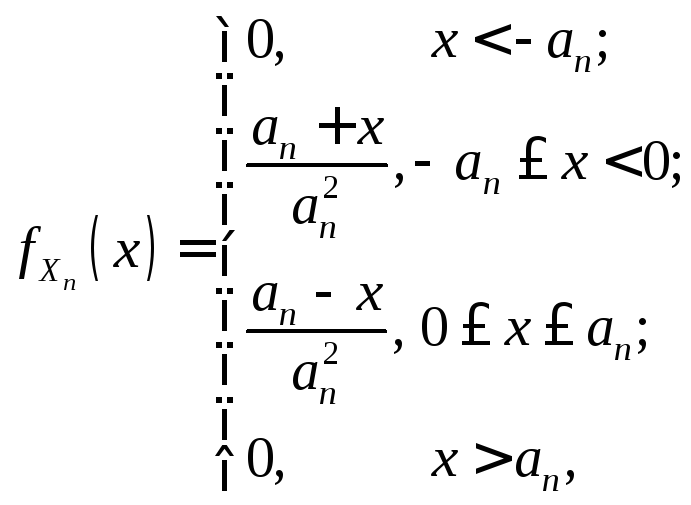
причем Подчиняется ли последовательность таких случайных величин закону больших чисел?

3.1.26. Случайные величины независимы и равномерно распределены а) на отрезкеб) на отрезкахсоответственно, причем, гдеи- положительные постоянные. Подчиняется ли эта последовательность случайных величин закону больших чисел?

3.1.27. Доказать, что, если - последовательность независимых случайных величин, имеющих дисперсии, удовлетворяющие условиюпри, то эта последовательность подчиняется закону больших чисел (теорема Хинчина).

3.1.28. Подчиняется ли закону больших чисел последовательность независимых случайных величин , если, гдеc>0, >0 - некоторые постоянные?

3.1.29. Показать, что, если последовательность случайных величин , такова, чтои,ki, , то она подчиняется закону больших чисел.

3.1.30. Дана последовательность случайных величин , для которых,(- коэффициент корреляции междуи). Доказать, что эта последовательность подчиняется закону больших чисел (теорема Бернштейна).

3.1.31. Пусть - последовательность случайных величин такая, чтоможет зависеть только оти, но не зависит от всех других. Показать, что для этой последовательности закон больших чисел выполняется, если,.

3.1.32. Доказать, что если функция непрерывна в точкеa и последовательность случайных величин , такова, чтопри, топри.

3.1.33. Доказать, что если последовательность случайных величин , такова, что,ипри, то ипри.

3.1.34. Доказать, что если последовательности случайных величин , таковы, чтопри, то

а) ; б)при.

3.1.35. Вычислить

,

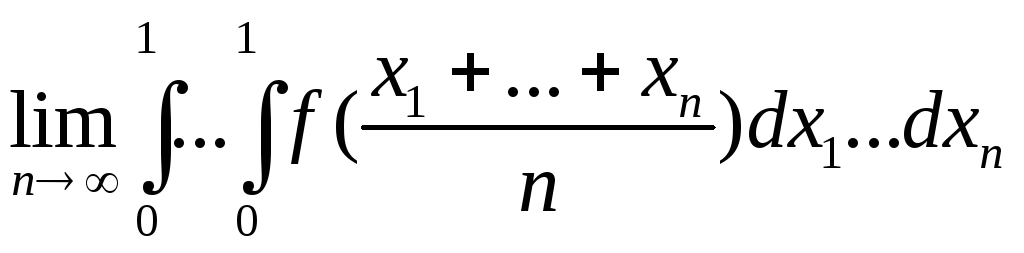если - функция, непрерывная на отрезке.

3.1.36. Доказать, что

,

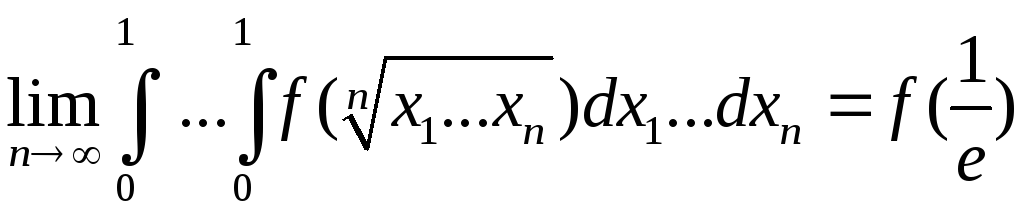где - функция, непрерывная на отрезке.

3.1.37. Последовательность независимых случайных величин удовлетворяет условиям:

, ,.

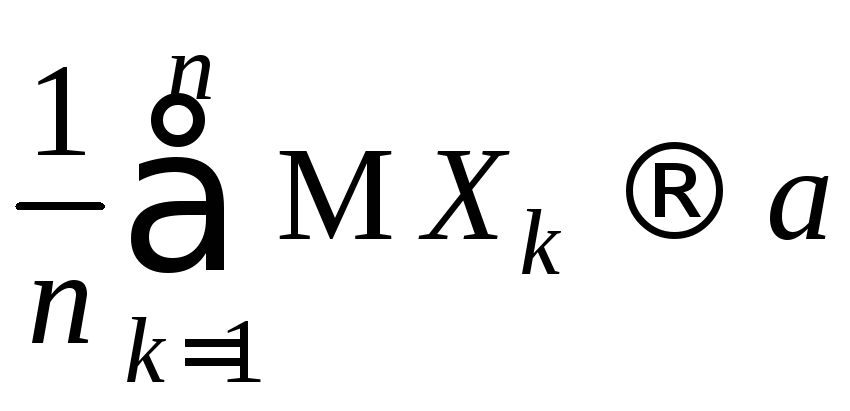Доказать, что для произвольной непрерывной и ограниченной на всей числовой прямой функции f(х) имеет место равенство:

.
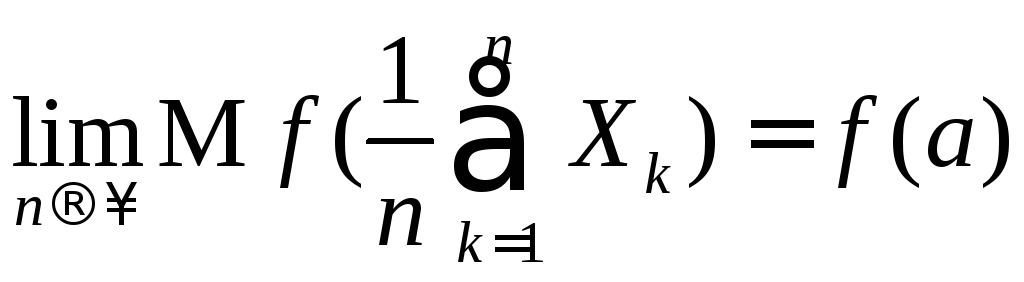