
САПР
.pdf
Позволяет уменьшить вычислительные затраты по сравнению с обычным сканированием при одинаковой точности отыскания экстремума, но появляется опасность "потери" глобального экстремума, особенно на начальных этапах поиска.
4.2. Метод Монте-Карло ( ММК )
Суть алгоритма ММК - последовательный анализ случайно выбранных точек в области допустимых проектных переменных.
Достоинства.
Простота и регулярность алгоритма, возможность отыскания глобального экстремума.
Недостатки.
Большие вычислительные затраты, отсутствие четких критериев останова.
4.2.1. Поэтапная реализация ММК
Для уменьшения вычислительных затрат оптимизацию по ММК разделяют на этапы с последовательным уменьшением области поиска (гиперкуба поиска).
На первом этапе центр гиперкуба поиска обычно помещают в |
центр допустимой |
области, а величину ребра гиперкуба выбирают такой, чтобы |
грани гиперкуба |
совпадали с границами допустимой области. |
|
На каждом последующем этапе центр гиперкуба помещается в точку лучшей пробы предыдущего этапа, при этом ребро гиперкуба постоянно уменьшается от этапа к этапу, пока его длина не станет меньше наперед заданной величины.
4.3. Вопросы для тренинга и самоконтроля http://cnit.ssau.ru/kadis/optim/Text/4_3.html
11

5. Направленный поиск
Методы направленного поиска используют рекуррентную (возвратную) зависимость
|
X(k+1) = X(k) + X(k), |
где X(k) |
- точка, полученная на k-1 этапе поиска; |
X(k+1) |
- точка после k-го этапа поиска; |
X(k) |
- вектор приращений проектных переменных на k-ом этапе поиска; |
|
X(k) = (k)t(k), |
где (k) = ( 1(k), 2(k), ... , i(k), ... , n(k)) - направляющий вектор единичной длины, указывающий направление движения поисковой точки на k-ом шаге поиска;
t(k) = X(k+1) - X(k) - длина шага на k-ом этапе (рис.ниже).
5.1. Покоординатная оптимизация
Суть алгоритма - поочередное варьирование каждой переменной при фиксированных значениях остальных.
Выбирают начальную точку и переменную, которую будут варьировать первой. Выполняют спуск
(одномерную оптимизацию) вдоль выбранной переменной. Из найденого экстремума функции одной переменной проводят спуск вдоль другой переменной и т.д. (рис.5.1)
12

Поиск заканчивают, когда малые пробные шаги во всех направлениях внутри допустимой области не приводят к уменьшению функции цели.
Достоинства.
Простота и регулярность алгоритма, высокое быстродействие на регулярных участках рельефа целевой функции.
Недостатки.
Низкая эффективность в "оврагах", "застревание" на границах.
5.2. Градиентные методы
Это методы направленного поиска, использующие рекуррентную формулу
X(k+1) = X(k)+ (k)t(k)
Направляющий вектор (k) - выбирается вдоль антиградиента целевой функции
(k) = - f(X(k)) / f(X(k)) ,
где f(X(k)) - вектор градиента целевой функции,f(X(k)) - его длина,
f(X(k)) = ( f(X(k))/ x1, f(X(k))/ x2,…, f(X(k))/ xi,…, f(X(k))/ xn)
5.2.1. Градиентный метод простых итераций
Движение поисковой точки производится вдоль антиградиента целевой функции, вычисляемого на каждом шаге, с длиной шага, равной постоянной фиксированной величине t.
При t 0 ломаная траектория движения превращается в плавную линию, ортогональную поверхностям равного уровня (рис).
13

Метод неэкономичен, так как требует вычисления составляющих f(X(k)) в большом числе точек.
5.2.2. Метод наискорейшего спуска
Это градиентный метод направленного поиска.
Движение поисковой точки на каждом шаге производится вдоль антиградиента целевой функции до тех пор, пока целевая функция убывает, т.е. производится одномерная
оптимизация вдоль - f(X(k)). При этом направления поиска на смежных шагах являются ортогональными друг другу.
Достоинства.
Высокое быстродействие на регулярных участках рельефа целевой функции.
Недостатки.
Низкая эффективность в "оврагах".
14
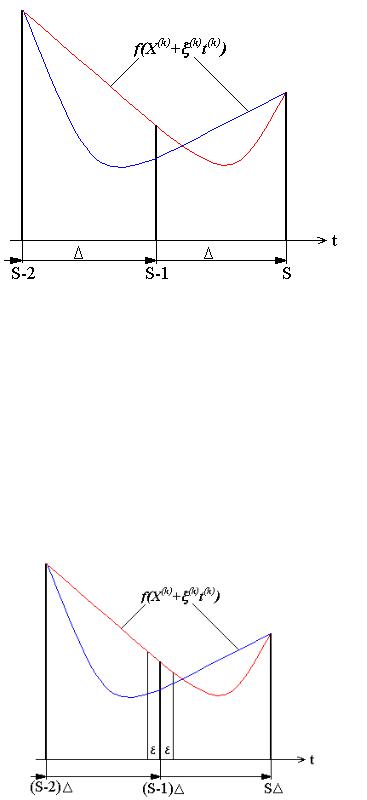
5.3. Шаговый метод одномерного поиска
Используют в методах покоординатной оптимизации и наискорейшего спуска.
В направлении движения поисковой точки делают шаги длиной и анализируют
значения функции f(X(k)+ (k)t(k)) после каждого шага. Процесс пошагового
спуска останавливают, как только анализируемая функция начнет увеличиваться.
При этом появляется интервал неопределенности длиной L = 2 , внутри которого располагается экстремум (рис.ниже).
На рисунке S - текущий номер шага при спуске по t.
5.3.1. Дихотомия
Используется для уменьшения интервала неопределённости, полученного в шаговом методе.
Определяется угол наклона графика f(X(k)+ (k)t (k)) в средней точке интервала, знак опеределяется по выражению
f(X(k)+ (k)((S-1) + )) - f(X(k)+ (k)((S-1) - ))
При знаке "+" новый интервал ((S-2) , (S-1) + )
При знаке "-" новый интервал ((S-1) - , S ) (рис.ниже).
15

5.3.2. Метод золотого сечения
Используется для уменьшения интервала неопределенности в шаговом методе одномерного поиска.
Основан на магическом числе T=0,618. Суть метода ясна из рисунка (рис.5.5).
Золотое сечение является более экономичным методом, чем дихотомия.
5.4. Метод конфигураций Хука-Дживса
Предназначен для поиска экстремума в зонах нерегулярного поведения функции цели ("овраги","изломы" и т.п.).
Сочетает в себе так называемый "исследующий" поиск для выявления локального характера поведения целевой функции и рабочие шаги вдоль найденного направления.
Пробные шаги в исследующем поиске делают вдоль осей координат, уменьшая их вдвое, если после исследования по всем координатам направление спуска не обнаружено
16

Критерий останова - достижение заданной (малой) величины пробного шага исследующего поиска.
5.5. Метод деформируемого многогранника Нелдера-Мида
Вn-мерном пространстве проектных переменных строят многогранник
сn+1 равноотстоящими друг от друга вершинами. Определяют значения целевой функции в вершинах многогранника. Вершину с наибольшим значением целевой функции переносят (отражают) через центр тяжести остальных вершин (рис.5.7). В ходе таких шагов осуществляют спуск в направлении минимума.
В ходе спуска многогранник может растягиваться в зонах плавного убывания целевой функции и сжиматься в окрестностях оврагов и локальных экстремумов. Эвристические правила деформирования многогранника приведены на рис.ниже..
Критерий останова: |
F = (Fmax - Fmin)/Fmin < , |
5.6. Вопросы для тренинга и самоконтроля http://cnit.ssau.ru/kadis/optim/Text/5_6.html
17

6. Методы направленного случайного поиска (СП)
Используют рекуррентную формулу
X(k+1) = X(k)+ (k)t(k),
где (k) определяют с использованием элементов случайности.
Вдали от экстремума методы СП обладают большим быстродействием, чем градиентные методы. С ростом размерности задачи преимущества СП становятся всё более ощутимыми.
Различают две группы CП: с самообучением и без самообучения.
6.1. Самообучение в методах случайного поиска
Информацию о ходе поиска в этих методах хранят в векторе памяти
W(k) = W(k-1) - ( f(X(k-1)))X(k-1),
На каждом этапе направление вектора W(k) указывает предпочтительное направление
дальнейшего движения, а его длина W(k) характеризует степень достоверности информации, полученной в ходе предыдущего поиска.
Коэффициент забывания в диапазоне (0,1) определяет глубину памяти алгоритма,
при =1 забывания нет, при =0 память отсутствует полностью и учитывается только последний шаг.
Параметр обучения ( >0 ) позволяет изменять относительный вклад информации, полученной на последнем шаге по отношению к накопленной и сохранённой старой информации.
f(X(k-1)) - приращение (убывание) целевой функции на k-1 шаге поиска.
6.2. Вектор памяти в направленном случайном поиске
При использовании вектора памяти поисковая точка движется вдоль
вектора (k) (см. рис.6), где - случайный нормированный вектор с равномерным распределением по всем направлениям пространства проектных переменных.
Таким образом, возможные
направления (k) концентрируются вокруг вектора памяти, выражающего некоторую статистику наилучшего направления, накопленную в результате предыдущего поиска.
При слабой обученности алгоритма длина W(k) уменьшается, вследствие чего расширяется область возможных
направлений (k). Наоборот, чем обученность полнее (W(k) больше), тем уже область возможных
направлений (k) и целенаправленнее поиск.
6.3. Вопросы для тренинга и самоконтроля http://cnit.ssau.ru/kadis/optim/Text/6_3.html
18

7. Влияние ограничений
При решении реальных задач оптимизации нередко возникает ситуация, показанная на рис.7.1. Поисковая точка, перемещавшаяся по координатам, на некотором шаге "застревает" на границе ограничения. Но экстремальная точка не достигнута, потому необходимы последующие итерации.
Рассмотрим два подхода, приводящих к движению поисковой точки вдоль границы допустимой области.
7.1. Метод зигзагообразного движения
В этом методе при нарушении хотя бы одного ограничения и выходе поисковой точки за пределы допустимой области производится возврат в область по направлению антиградиента нарушенной ограничительной функции.
Характерный вид траекторий зигзагообразного движения показан на рис.
7.2. Метод проекции градиента
Основная идея метода проекции градиента заключается в выборе (k) вдоль проекции антиградиента целевой функции на плоскость нарушенного ограничения (рис.ниже,верх).
Если же нарушенное ограничение нелинейно, то антиградиент проецируется на гиперплоскость, касательную к поверхности ограничений (рис.ниже, низ). После
проведения шага вдоль (k) в случае выхода за пределы предусматривается возвращение в по антиградиенту ограничения.
19

7.3. Критерии завершения поиска
В теории оптимизации существует теорема Куна-Таккера, в которой математически строго определяются необходимые и достаточные условия достижения экстремума.
Однако, во многих практических задачах используют приближенные критерии.
Вметодах направленного поиска это два признака:
1)достижение минимальной длины шага;
2)достижение минимального приращения (убывания) целевой функции за один шаг.
Эти критерии в ряде случаев позволяют идентифицировать локальный экстремум или его окрестность. Или же, что ошибочно может быть принято за минимум, русло "оврага" вдали от экстремума.
Глобальный экстремум выявляется путем проведения ряда повторных спусков из различных начальных точек.
7.4. Вопросы для тренинга и самоконтроля http://cnit.ssau.ru/kadis/optim/Text/7_4.html
20
