САПР

Современные системы автоматизированного проектирования (САПР) Offline-учебник. (под редакцией А. В. Соловова)

1. Формулировка проектных задач

"Четко поставленная задача - наполовину решенная задача"

Задачи оптимального проектирования формулируются в терминах математического программирования - раздела прикладной математики, занимающегося изучением экстремумов функций и разработкой методов отыскания этих

экстремумов. Владение терминологией математического программирования является частью математической культуры инженера и позволяет четко формулировать проектные задачи.

1.1. Функция цели

Это та характеристика проектируемого изделия, экстремальное значение которой (минимум или максимум) необходимо обеспечить в процессе проектирования.

Целевую функцию обозначают f(X), где X - вектор проектных переменных.

Примерами целевых функций являются стоимость, масса, прочность, габариты, коэффициент полезного действия и т.п.

1.2. Проектные переменные

Это те характеристики проектируемого изделия, величины которых варьируют с целью увеличения или уменьшения функции цели.

Проектные переменные обозначают

х1, ... , xi, ... , xn,

а всю их совокупность называют вектором проектных переменных

X = (х1, ... , xi, ... , xn).

Количество проектных переменных n характеризует степень сложности и трудоемкости проектной задачи. Оно может принимать значения от n = 1 до нескольких тысяч и даже десятков тысяч. Увеличение n увеличивает сложность и трудоемкость процесса оптимизации.

1.3. Ограничения

Это некоторые зависимости (ограничительные функции), определяющие предельные значения характеристик проектируемого изделия с точки зрения условий его изготовления и эксплуатации.

Ограничения записывают в форме слабых неравенств gj(X) 0, j = 1, 2, ... , m.

Количество ограничений m может быть любым. Увеличение m нередко увеличивает сложность и трудоемкость процесса оптимизации.

1.3.1. активные и пассивные ограничения

Если в экстремальной точке одно или несколько ограничений gj(X) 0

выполняются в виде равенства gj(X) = 0,

то эти ограничения называют активными.

В противном случае

(gj(X) < 0 или gj(X) > 0 )

ограничения называют пассивными.

1

1.7. Основные этапы формулировки

1.Выбор целевой функции f(X).

2.Выбор проектных переменных X = ( x1, x2, ... ,xi, ... ,xm).

3.Запись ограничений gj (X) 0, j = 1, 2, ... , m.

4.Выбор математической модели (не всегда).

5.Математическая запись задачи, например:

минимизировать f(X) при ограничениях gj(X) 0, j = 1, 2, ... , m.

Примеры формулировок задач

3

1.8. Неформальные советы

При выборе целевой функции основная проблема заключается не в том, чтобы из различных критериев (массы, стоимости, надежности, прочности и т.п.) выбрать единственный, а остальные критерии представить в виде ограничений, сколько в том, чтобы задать конкретные предельные значения ограничительных функций.

При выборе проектных переменных необходимо увеличивать их количество, чтобы охватить потенциально наибольшее число возможных проектных решений.

С другой стороны требование уменьшения вычислительных затрат заставляет уменьшать размерность пространства проектных переменных.

Для решения этих и ряда других вопросов не существует формальных подходов. Проектировщик должен обладать профессиональным

опытом, "инженерным чутьем", опирающимся на глубокие знания как свойств объектов проектирования, так и методов их оптимизации.

1.9. Геометрическая интерпретaция задач оптимизации

1.n - размерность пространства проектных переменных.

2.X = ( x1, x2, ... , xn) - координаты точки n - мерного пространства.

3.gj(X) = 0 - гиперповерхность ограничительной функции.

4.= ( X : gj(X) 0, j = 1, 2, ... , m ) - область допустимых проектных решений пространства проектных переменных (допустимая область).

5.f(X) = C - гиперповерхность равного уровня функции цели (см.рис.).

1.9.1. Двумерный случай

Если задача оптимизации имеет две проектные переменные X = ( x1, x2) и простой аналитический вид целевой и ограничительной функций, то ее можно изобразить на плоскости и решить графически.

Сначала в системе координат x1Ox2 проводят линии равного уровня функции цели. Затем - графики функций gj(X) = 0. Далее штриховкой выделяют границы

области допустимых проектных переменных и внутри этой области или на её границе отыскивают экстремальную точку (рисунок выше + ниже)

4

1.10. Вопросы для тренинга и самоконтроля

http://cnit.ssau.ru/kadis/optim/Text/1_10.html

5

2. Классификация методов оптимизации

Методы оптимизации Аналитические

Поисковые Ненаправленный поиск

Направленный поиск Методы детерминированного поиска

Методы случайного поиска

2.1. Поисковые и непоисковые методы

Непоисковые (аналитические) методы

1.Связаны с классической математикой (дифференциальное и вариационное исчисления).

2.Процесс решения - аналитический.

3.ЭВМ практически не используются.

Поисковые методы

1.Связаны с математическим программированием.

2.Процесс решения - численный.

3.Широко применяются ЭВМ.

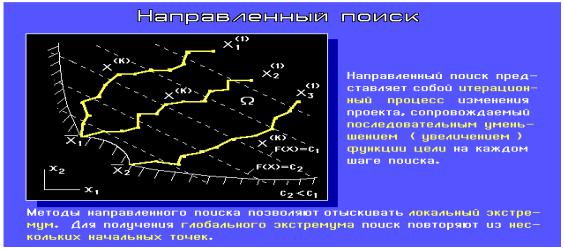
2.2. Направленный поиск

Методы направленного поиска используют рекуррентную (возвратную) зависимость

X(k+1) = X(k) + X(k),

где (k) = ( 1(k), 2(k), ... , i(k), ... , n(k)) - направляющий вектор единичной длины, указывающий направление движения поисковой точки на k-ом шаге поиска;

t(k) = X(k+1) - X(k) - длина шага на k-ом этапе (рис).

6

3. Аналитические (непоисковые) методы. Метод неопределенных множителей Лагранжа

L(X, ) = f(X) + ig i(X),

где =( 1, 2, …, m) - вектор неопределенных множителей Лагранжа.

Для отыскания экстремума функции L(X, ) составляется система m+n уравнений с n неизвестными Xi, и m неизвестными i .

…………………………….

L(X, )/ xi = f(X)/ xi+ j( gj/ x i)=0, i=1, 2, …, n…………………………….

L/ j=g j(X)=0, j=1, 2, …, m…………………………….

Компоненты искомого вектора X0 находятся среди корней этой системы.

3.1. Геометрическая интерпретация метода Лагранжа

Приведём теперь простую геометрическую интерпретацию метода множителей Лагранжа для двухпараметрической задачи с одним ограничением.

На рис.ниже изображены линии равного уровня функции f(X), где X=(x1,x2), и ограничение g(X)=0.

8

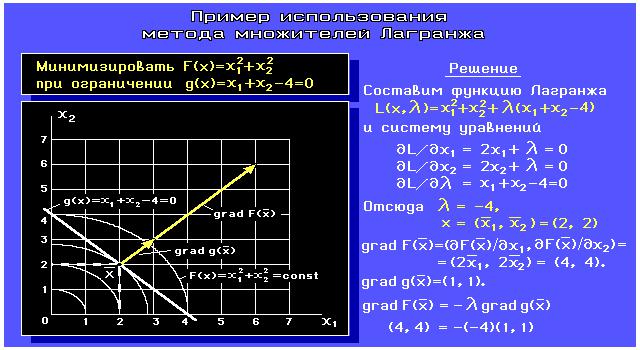
Рассмотрим пример использования метода множителей Лагранжа (рис. ниже).

3.2. Вопросы для тренинга и самоконтроля http://cnit.ssau.ru/kadis/optim/Text/3_2.html

9

производится последовательное улучшение проекта на каждом шаге. Но рекуррентная формула

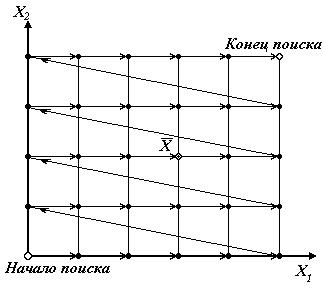
4.1. Сканирование по сетке

Суть метода - упорядоченный перебор вариантов проекта.

Область допустимых проектных переменных разбивают сеткой, по узлам которой проводят сканирование, при этом в каждом узле вычисляется функция цели.

Построчная прогонка

Фиксируют все переменные, кроме одной, и исследуют проектную область вдоль одной строки, т.е. меняя одну переменную; затем переходят на другую строку и т.д.

Достоинства.

Простота и регулярность алгоритма, возможность отыскания глобального экстремума.

Недостатки.

Большие вычислительные затраты.

4.1.1. Поэтапное сканирование

На первом этапе проектную область разбивают сеткой с крупным шагом, проводят сканирование и находят узел сетки с наименьшим значением функции цели.

На втором этапе окрестность найденного экстремума разбивают более мелкой сеткой, проводят на ней сканирование, находят на ней экстремум, измельчают вокруг него сетку и т.д. (рис.4.2).

10