Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Синтез_мех_систем

.pdf

Скачиваний:

Добавлен:

16.03.2015

Размер:

2.5 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

где: ui - малая величина, называемая пробным шагом.

Этот метод чрезвычайно прост для программирования и требует наи-

большего объема памяти машины. Недостатком его является то, что он мо-

жет давать большие погрешности.

4.5.2 Метод интегрирования уравнений чувствительности.

Пусть, например, управляющий процесс описывается уравнениями:

dxi	fi	(t, x,u), xi (0) xi 0 , i 1,2...n	(4.5.2)
dt

Дифференцируя эти уравнения по параметрам ui, получим систему для определения функций чувствительности

dzij (t)	n
	n
	ik zkj	ij ; zij (0) 0	(4.5.3)
dt	ik zkj	ij ; zij (0) 0	(4.5.3)
dt	k 1

где: z		xi	,		fi	,		fi	, i, j 1,2,...n
	ij	u j		ik	xk		ij	u j

Используя уравнения (4.5.3) можно с высокой точностью определить ча-

( n)

стные производные

. Пусть, например,

( n)

f [x(t1 )]. Тогда

u j

( n)

(t )

, при этом

находятся аналитически, а z

) - из ре-

u j

i 1

шения уравнения (4.5.2).

4.6 Метод случайного поиска

Опыт использования численных методов показывает, что определение градиента функции ( u ) связано со значительными трудностями. Поэтому наряду с детерминированными методами поиска на практике используют ме-

тоды случайного поиска, которые свободны от указанного недостатка, [ ]. В

методах случайного поиска направление шага, а иногда и величина, опреде-

ляются случайным образом.

Этот метод является прямым развитием известного метода проб и оши-

бок, когда решение ищется случайно, и при удаче принимается, а при неуда-

че отвергается с тем, чтобы немедленно снова обратиться к случайности как к источнику возможного. Такое «случайное» поведение разумно опирается на уверенность, что случайность содержит в себе все возможности, в том числе и искомое решение.

Итерационный алгоритм поиска оптимальных параметров представим в

виде: u ( n 1) u ( n )

u ( n 1) .

4.7 Метод градиента для задачи с функциональным и параметрическим

управлением

Для определенности построим алгоритм градиентного спуска для ОЗУ с конкретным числом критериев в формулировке задачи прохождения фазовой


траектории через дискретную "трубку".
		Положим,	что	при	каком–то управлении					из	допустимой области
		(t) U 2 , a Am	в соответствии с управлениями (3.1.2)								из всей совокупности
	u	(t) U 2 , a Am	в соответствии с управлениями (3.1.2)								из всей совокупности
безразмерных функционалов íj							(t), a и íj		(t), a ,	i=1, 2… …n; j=1,2…S…;
безразмерных функционалов íj						u	(t), a и íj	u	(t), a ,	i=1, 2… …n; j=1,2…S…;
наибольшим является функционал, соответствующий											ой фазовой координате
в сечении t=tS, т.е.				s , или	s .

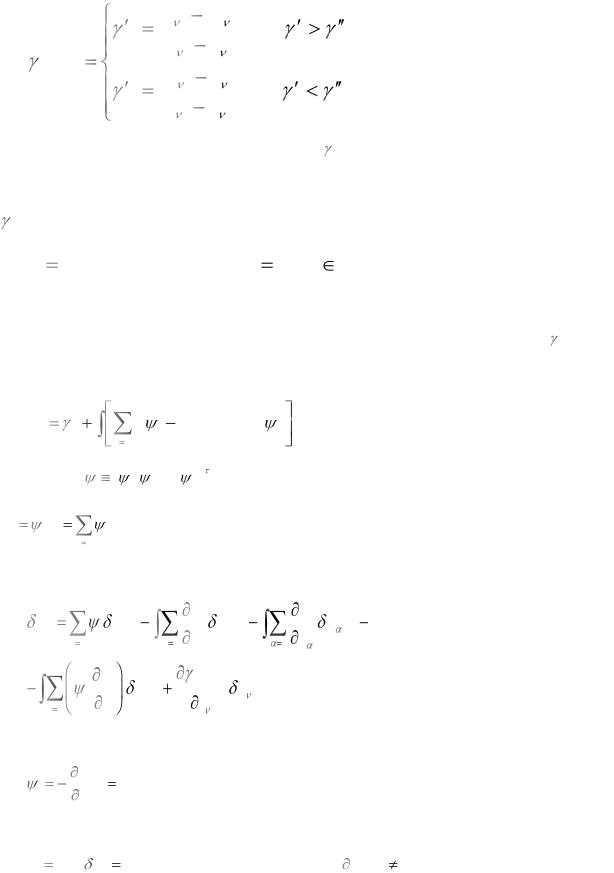
Введем обозначение

	'	A s	X s
q		A s	a s
q ts
		X s	a s
	'
q		A s	a s

,при

q q

(4.7.1)

q q ,

и будем рассматривать функционал

q ts

как функционал вариационной

задачи

в форме майера,

[9],

т.е. будем

минимизировать функционал

q ts ,

(t), a , при дифференциальных связях

f (t, x (t), u (t), a ), x

X 0 , t

0,TA

(4.7.2)

Согласно вариационной теории это задача на условный экстремум и ми-

нимизироваться должен равносильный исходному функционалу

функ-

ционал следующего вида

i H

t, x,u , a, dt.

(4.7.3)

Здесь

2 ,...,

– вектор–функционал

сопряженных

координат,

i fi

t, x,

, a

– функция Гамильтона.

i 1

Вариация функционала Jq имеет следующий вид [16]:

ts m

a dt

1 u

i 1

0 j 1

(4.7.4)

xi dt

x ts

0 i 1

Определим сопряженные переменные из дифференциальных уравнений

, i

1, 2,..., n,

(4.7.5)

учитывая,

что

левый

конец

фазовой

траектории фиксирован

x 0

0 , а правый свободен, т.е. x

0 , будем иметь:

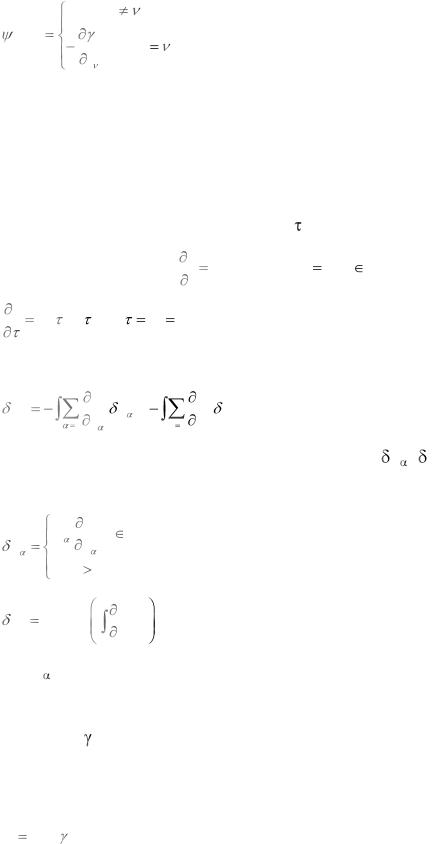
0, если i

i ts	q	, если i	,	(4.7.6)
	x	, если i	,
	x

Интегрируя уравнения (4.7.5) в "обратном" времени, т.е. справа на лево с начальными условиями (4.7.6) сопряженные координаты могут быть опреде-

лены.

Интегрирование в "обратном" времени осуществляется при помощи вве-

дения новой независимой переменной =ts–t. Например, для одного диффе-

ренциального уравнения			y	f t, y(t) , y(ts ) yk	,t 0,ts	будем иметь

			t
			t
	y	f , y( ) , y( 0)	yk .

Теперь вариация функционала примет следующий вид

ts r

0 1

H	ts	m	H
	u dt			a j dt	(4.7.7)

u		j 1 a j
	0

Чтобы вариация была меньше нуля, поправки u , аj выбираются из ус-

ловия

K	H		, t		0, ts
	u					(4.7.8)
u
0,	t	ts
		ts		H
a j K j Sign					dt ,	(4.7.9)

		0		a j

где К , Кj – малые положительные величины.

Выражения (4.7.8, 4.7.9) являются условиями, уменьшающими значение

функционала q.

С учетом изложенного имеем следующую процедуру операций для

уменьшения функционала

Г max		]	(4.7.10)
	q [u, a, ts
q, S

1. Из каких-либо соображений выбираем начальное приближение управ-

ляющих переменных из допустимой области


	(0)	{u	(0)	,u	(0)	...u	(0)		T	,	(0)	U	r
u		{u		,u	2	...u	r		}	,	u	U
(0)		1			2		r
(0)		{a	(0)	, a	(0)	...a		(0)	T	,		m
a		{a		, a		...a			}	,	a	A
		1			2		m

2. Интегрируем основную систему дифференциальных уравнений (4.7.2),

определяющую значение фазовых координат				при начальных условиях
определяющую значение фазовых координат			x(t)	при начальных условиях	x0
с управляющими переменными u	(t), a	.
(0)	(0)

3. Вычисляем начальное приближение значений функционалов из задан-

ной совокупности q	[u	, a	, ts ], q 1, 2,...n, s 1, 2,...,	и находим из них наи-
	(0)	(0)

больший.

4. Интегрируем сопряженную систему дифференциальных уравнений

(4.7.5, 4.7.6) в "обратном" времени при найденных значениях фазовых коор-

динат и начальном приближении управления. Находим начальное приближе-

ние сопряженных координат

(0)

{

1 ,

2 ,...

} .

5. Вычисляем производные функции Н по переменным

u при u(0)

и инте-

грала

при значениях

(0)

и находим поправки

, u

, a

a j

u(1) , a(1)j , уменьшающие значение функционала (4.7.10)

u(1)

x( 0 ) , ( 0 ) ,u( 0 ) ,a( 0 )

(4.7.11)

a(1)

k sign(

dt)

aj x( 0 ) , ( 0 ) ,u( 0 ) ,a( 0 )

6.Формируем и запоминаем первое приближение управляющих перемен-j j

ных

		(0)	(0)	, t	[0,ts	]
	(1)	u	u	, t	[0,ts	]
u		0		,t	ts	(4.7.12)
		0		,t	ts	(4.7.12)
(1)		(0)	(0)
a		a	a

7. Интегрируем основную систему (4.7.2) с управлением первого прибли-

жения и находим первое приближение фазовых координат.

8. Вычисляем значения функционалов и заданной совокупности и прове-

ряем выполнение условия

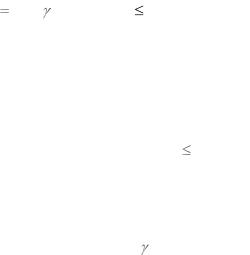
Г max			(1)		(1) ,t	] 1	(4.7.13)
Г max	q	[u	(1)	, a	(1) ,t	] 1	(4.7.13)
a, q	q				s
a, q

Если условие (4.7.13) выполняется, то это будет одно из решений постав-

ленной задачи. Если нет, процедура должна быть повторена, начиная с пунк-

та 3 до нахождения решения.

Выполнение условий Г 1 решает поставленную задачу, но не наилуч-

шим образом. Для определения более эффективного управления необходимо продолжить последовательность вычислительных операций, пока последую-

щее приближение max 1 практически не будет отличаться от предыдущего,

q, s

т.е. пока не будет найдено решение минимаксной задачи.

В заключение необходимо отметить, что те особенности решения ОЗУ с параметрическим управлением, связанные с "овражной" ситуацией, рассмот-

ренные в разделе 4.4, присущи и для данного случая. Поэтому, каждая кон-

кретная задача будет требовать конкретных всесторонних исследований.

5. Приложение математических методов решения задач управ-

ления к проектированию систем

5.1 Решение задачи отделения космических аппаратов от последней

ступени ракеты-носителя

5.1.1 Основные технические требования к процессу отделения

При осуществлении операции отделения одного или нескольких КА от последней ступени ракеты-носителя (в дальнейшем просто РН), кроме требо-

ваний надежного и безотказного срабатывания всех элементов, осуществ-

ляющих разделение и отделение, должно быть обеспечено выполнение цело-

го ряда требований кинематического характера.

Отделение должно происходить безударно, т. е. любые соприкосновения конструкции КА и РН после срабатывания системы отделения недопустимы.

Приращение угловой скорости КА за счет срабатывания системы отделения должно быть минимальным. Это требование обычно задается в виде нера-

венств ограничивающих величину приращения угловой скорости в проекци-

ях на связанные с КА оси координат. Кроме того, относительные скорости расхождения после срабатывания системы отделения должны исключать возможность столкновения КА между собой и с РН при орбитальном полете.

Могут также предъявляться требования по обеспечению заданного расстоя-

ния между КА и РН через определенный промежуток времени после отделе-

ния, или требование по увеличению расстояния между КА на каждом витке траектории на заранее заданную величину.

Эти требования обычно задаются конкретно для каждого класса КА в за-

висимости от их назначения и особенности работы на орбите.

5.1.2 Математическое описание процесса отделения и последующего дви-

жения

В начале рассмотрим движение КА и РН на «ближнем» участке расхож-

дения, т. е. на участке непосредственно срабатывания энергетических средств, осуществляющих отделение. На практике, в большинстве случаев, в

качестве таких средств используются пружинные толкатели. Их корпуса же-

стко закреплены на переходном отсеке (ПхО) РН так, что продольная ось корпусов совпадает с направлением отделения КА.

Количество толкателей выбирается на стадии формирования структурной схемы системы отделения. Из условий рациональности компоновки и сим-

метрии отделения их может быть 3, 4 или 6 штук. Поскольку относительное расстояние между КА и РН при срабатывании толкателей мало, будем счи-

тать, что движение РН и КА происходит только под действием усилий толка-

телей в инерциальной системе координат, которая вместе с ц.м. системы КА

+ РН движется с орбитальной скоростью. Иными словами, кривизной поля тяготения пренебрегаем. КА и РН считаем абсолютно твердыми телами по-

стоянного состава.

Будем считать, что усилие пружинного толкателя является линейной функцией перемещения его штока, т. е. F ( ) Fo c ; где Fo – начальное

усилие, с – жесткость пружины толкателя, – перемещение пружины толка-

теля. Диаграмма усилия толкателя представлена на рисунке 5.1.

Рисунок 5.1 – Диаграмма усилия толкателя Здесь Fk – конечное усилие толкателя, h – полный ход штока.

Fо – начальное усилие толкателя.

Перемещение штока толкателя по времени и направление действия силы в пространстве будут определяться кинематическими параметрами относи-

тельного движения КА и РН.

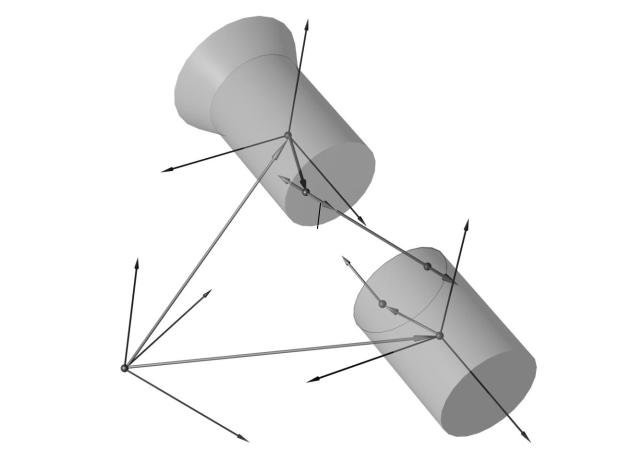
Расчетная схема процесса отделения на участке работы толкателей приве-

дена на рисунке 5.2. Здесь изображен случай отделения одного КА от РН под действием одного толкателя (случай отделения нескольких КА принципи-

альных изменений не вносит).

aП0

zи

ц.м. ОИ

xи
xи			rA
			rA

		F А			yи		zКА

zo	R	И			ao
zo					И
					И

					aПo
		yo			aПo		F

						rП
							ц.м.
		RКА					ц.м.
							ОКА
				xКА
		xo						yКА
		xo

Рисунок 5.2 – Расчетная схема процесса отделения на участке работы тол-

кателей

На рисунке показаны: xoyozo – инерциальная система координат, xиyиzи, xКАyКАzКА – связанные системы координат, начало которых совпадает с ц. м.

КА и РН соответственно, - единичный вектор нормали плоскости П в с. к.

xКАyКАzКА (плоскость стыковочного шпангоута КА); rП - радиус-вектор неко-

торой точки, принадлежащей плоскости П; aИ0 - единичный направляющий вектор прямой в xиyиzи совпадающей с продольной осью толкателя; rA - ради-

ус-вектор точки А, совпадающей в начальный момент с концом штока толка-

теля.

Уравнение прямой в xиyиzи, совпадающей с продольной осью толкателя

имеет следующий вид:							o		, где – параметр. Уравнение этой пря-
имеет следующий вид:				r		r	a	И	, где – параметр. Уравнение этой пря-
						A		И
мой в инерциальной с. к. xoyozo:
			о t			(5.1.1)
R	A r	A a	о t	R	И	(5.1.1)
	И A	И	И		И

где: AИ – матрица перехода от xиyиzи к xoyozo.

Аналогично можно записать уравнение плоскости П в c. к. xКАyКАzКА и xoyozo, используя матрицу перехода от с. к. КА к с. к. инерциальной:

o							в xКАyКАzКА,
a	П	(r r ) 0					в xКАyКАzКА,
	П			П
A								0 в x y z
A			a o	(R	R	КА	A r )	0 в x y z	.	(5.1.2)
	КА		П			КА	КА П	o o o

Система уравнений (5.1.1), (5.1.2) определяет в любой момент времени

точку пересечения прямой и плоскости и значение параметра

, величина ко-

торого

равна

расстоянию

от

т.

вдоль

прямой

до

плоскости П, т. е. перемещению штока толкателя,

(t)=

(t).

Подставив R из (5.1.1) в (5.1.2) получим выражение для .

A a o

( A r A a

КА

A r ) 0,

КА П

КА

A a o

A r A a o

A a

A a o R

A a o

КА

A a o

A r 0,

КА П

КА

КА П

КА

(5.1.3)

AКА aП AИ rA

AКА aП AИ aИ

AКА aП RИ

AКА aП RКА

AКА aП

AКА rП

a o A a о

КА

Схема работы толкателя приведена на рисунке 5.3.

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.11.2019557.57 Кб13СИЗ.doc
#
29.03.20164.47 Mб129СИКПП-154.doc
#
29.03.20161.9 Mб57Силы_резания_NX_брошюра.pdf
#
11.11.2018843.26 Кб18Симановский Введение в информатику.doc
#
07.06.20152.2 Mб102СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ_2011.doc
#
16.03.20152.5 Mб43Синтез_мех_систем.pdf
#
16.03.2015162.3 Кб7СисПро ЛР1.doc
#
09.09.2019141.31 Кб1Система ипотечного кредитования.doc
#
16.03.20152.6 Mб216Система управления.doc
#
14.04.2019683.01 Кб14Системы искусственного интеллекта (старые лекци....doc
#
26.11.20196.64 Mб32Системы Ту-154В.DOC