
Дуплякин В.М. Теория игр
.pdf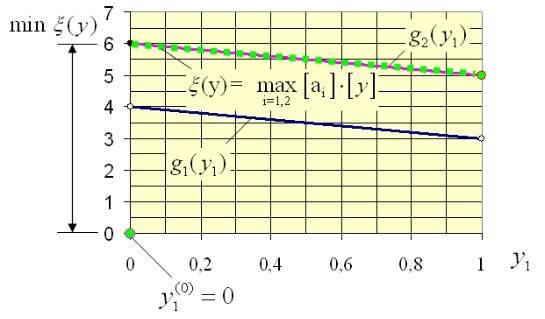
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
Рис. 7.4 – Формирование dominant-строки
Обобщая полученные результаты, можно утверждать, что условием доминирования столбцов и строк в играх 2х2 является отсутствие точек
пересечения в соответствующих плоскостях линий промежуточной скаляризации.
Вернёмся к данным ранее определениям:
"Если в некотором столбце платёжной матрицы все элементы меньше или равны соответствующим элементам другого столбца, то первый столбец доминирует второй и называется доминант-столбцом".
Эта ситуация отражена графически на рисунке 7.3, где видено, что
доминант-столбец |
éa1 |
ù |
, т.е. первая стратегия игрока Р2 всегда в данной игре |
|
|
ë |
û |
|
|
доминирует вторую стратегию éa2 |
ù . |
|||
|
|
|
ë |
û |
"Если в некоторой строке платёжной матрицы все элементы больше или равны соответствующим элементам другой строки, то первая строка доминирует вторую и называется доминант-строкой".
Почему именно так формулируется условие доминирования строк, поясняет графическая иллюстрация на рисунке 7.4, из которой видно, что
строка [a2 ] доминирует строку [a1 ] .
60
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
8. МАТРИЧНЫЕ ИГРЫ С НУЛЕВОЙ СУММОЙ 2хn И mx2 |
|
Матричные игры |
2 × n и m × 2 так же как и игры 2 × 2 имеют |
наглядную графическую иллюстрацию, в то время как для игр более высокой размерности графической иллюстрации нет.
8.1. Решение игр 2 × n
Рассмотрим решение матричных игр 2 × n , платёжная матрица которых
выглядит следующим образом
éa1,1 |
a1,2 |
... ... |
a1,n ù |
||
[A] = êa |
2,1 |
a |
... ... |
a |
ú. |
ë |
2,2 |
|
|
2,n û |
|
Теоретические аспекты решения данной задачи во многом совпадают с теорией решения игр 2 × 2, поэтому обратимся к решению конкретного примера с приведенной ниже платёжной матрицей размерностью 2 × 4
|
Платёжная |
|
|
Стратегии игрока Р2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
матрица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
[A] |
|
|
|
a1 |
|
|
a2 |
|
a3 |
|
a4 |
|
|
|
min |
|
|
max |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
Стратегии 1Ригрока |
|
a2 |
|
-4 |
|
2 |
|
1 |
|
-5 |
|
→ |
-5 |
|
|
|
|
|
||||
|
|
|
a1 |
|
|
2 |
|
|
-3 |
|
4 |
|
-1 |
|
→ |
|
-3 |
|
→ |
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓ |
|
|
↓ |
|
|
↓ |
↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
max |
|
|
|
2 |
|
|
2 |
|
|
4 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
min max |
|
-1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aˆ = max |
min |
{aij} = -3 |
|
- нижняя цена игры; |
||||||||||||||||
|
|
|
|
i=1,2 |
j=1,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
( |
|
|
|
max |
{aij} = -1 |
|
- верхняя цена игры. |
|||||||||||||
|
|
|
a = min |
|
|||||||||||||||||||
|
|
|
|
j=1,4 |
i=1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
61
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
Как видно из проведенного анализа нижняя цена не равна верхней, поэтому нет решения в чистых стратегиях, но по теореме Дж. фон Неймана есть оптимальное решение в смешанных стратегиях.
Рассмотрим смешанные действия первого игрока при фиксированных стратегиях второго игрока, что по существу является скаляризацией промежуточного этапа поиска решения данной задачи.
Вычислим частные платёжные функции вида, частные в том смысле, что игрок Р1 пользуется смесью стратегий [x1 ; x 2 ], а игрок Р2 применяет чистую
стратегию |
éa j |
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ë |
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
j |
= [x] ´ éa j ù |
при j = 1, 2, 3, 4, где |
|
[x] |
= [x |
1 |
; x |
2 |
] = [x |
1 |
; 1 - x |
1 |
]. |
||||||||||||||||||||
|
|
ë |
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
В рассматриваемом примере при заданных исходных данных получаем |
||||||||||||||||||||||||||||||||
|
|
l (x ) = [x ; 1- x ]´ |
é 2 ù |
= 2 × x -4 + 4 × x = 6× x -4; |
|
|
|
|||||||||||||||||||||||||||
|
|
1 |
1 |
|
|
1 |
|
1 |
|
ë-4û |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
ê |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
l (x ) = [x |
1 |
; 1- x |
1 |
]´ |
é-3ù |
= -3× x |
1 |
+2 - 2× x |
1 |
= -5× x |
1 |
+2; |
|
|
||||||||||||||||||
|
|
2 |
1 |
|
|
|
|
ê |
2 |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ë |
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l (x ) = [x |
1 |
; 1- x |
1 |
]´ |
é4ù |
= 4 × x |
1 |
+1- x |
1 |
= 3× x |
1 |
+1; |
|
|
|
|
|
|
|
|||||||||||||
|
|
3 |
1 |
|
|
|
|
ê |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ë1û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l (x ) = [x ; 1- x ]´ |
é-1ù |
= -x -5 + 5× x = 4 × x -5. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
4 |
1 |
|
|
1 |
|
1 |
|
ë |
-5û |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ê |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
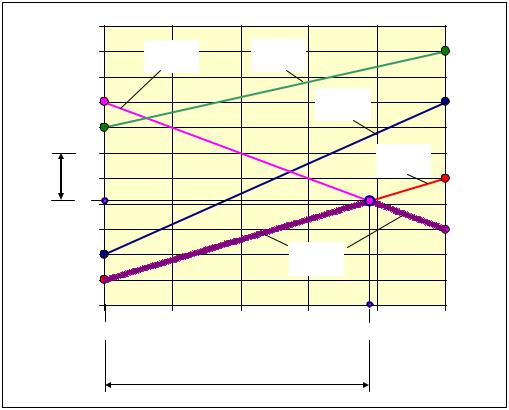
Графическое изображение полученных частных платёжных функций представлено на рис. 1.
Следующим этапом решения является построение кусочно-линейной
функции минимального выигрыша первого игрока
ψ(x1) = min{l1(x1);l2 (x1);l3(x1);l4 (x1)}.
Для построения этой функции следует воспользоваться графиком на рис. 8.1 и мысленно провести на нём произвольные вертикальные линии, нижняя из
полученных точек пересечения с частными платёжными функциями будет принадлежать искомой линии ψ(x1 ), как это показано на том же рисунке.
Наибольшее значение функции ψ(x1 ) даёт цену игры при оптимальном
решении
ν = max ψ(x1 ).
62
Т Е О Р И Я |
И Г Р |
|
|
|
|
|
|
В.М.Дуплякин |
|
|
5 |
l2 (x1) |
|
l3(x1) |
|
|
|
|
|
4 |
|
|
|
|
||
|
|
3 |
|
|
l1(x1) |
|
|
|
|
|
2 |
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
ν |
0 |
|
|
|
l4 (x1) |
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
-3 |
|
|
ψ(x1) |
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
x1 |
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
|
|
|
x(0) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Рис. 8.1 – Оптимизация смешанных стратегий игрока Р1 |
|||||||
Что бы найти оптимальную смесь стратегий игрока Р1 необходимо
обратиться к графическому представлению частных платёжных функций и найти те из них, пересечение которых даёт цену оптимальной игры ν = max ψ(x1 ). Из рис. 8.1 видно, что линиями, приводящими к оптимальным
стратегиям являются линии |
графиков |
частных платёжных функций |
||
l2 (x1 ) и l4 (x 1 ) . Приравняв уравнения |
|
этих линий, найдём оптимальное |
||
относительное содержание первой стратегии игрока Р1 |
||||
l (x(0) ) = l |
4 |
(x(0) ). |
||
2 |
1 |
|
1 |
|
Используя найденные ранее зависимости для платёжных функций,
запишем следующее
-5× x1(0) + 2 = 4 × x1(0) - 5.
Решая полученное уравнение, найдём оптимальное содержание первой
стратегии в смеси стратегий первого игрока
x1(0) = 79 = 0,77(7).
63
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
Как следствие этого решения имеем оптимальное относительное содержание второй стратегии игрока Р1
x2(0) = 1- x1(0) = 92 = 0,22(2).
Таким образом матрица выбора оптимальных стратегий игроком Р1
выглядит как
éx(0) ù = [0,77(7); 0,22(2)].
ë û
Цену оптимальной игры можно найти, подставив координату x1(0) в
уравнение одной из платёжных функций, соответствующих найденному оптимуму, например
ν = l4 (x1(0) ) = 4 ´ 79 - 5 = -179 = -1,88(8).
Следует обратить внимание на особенность полученного решения, которая заключается в отрицательном знаке цены оптимальной игры. Это означает, что игроки по сравнению с принятым распределением как бы поменялись ролями: Р1 проигрывает, а Р2 выигрывает.
Перейдём к выбору оптимальных смешанных стратегий игрока Р2. Воспользуемся тем обстоятельством, что оптимальное решение первого
игрока получено ранее при пересечении графиков частных платёжных функций
l2 (x1 ) и l4 (x 1 ) . Оказалось, что платёжные функции l1(x1 ) и l3 (x1 ) не задействованы при нахождении оптимального решения данной задачи. Поэтому
вместо исходной платёжной матрицы [A] можно ввести в рассмотрение
эквивалентную платёжную матрицу |
éA* ù |
, выполнив изъятие "ненужных" |
стратегий или столбцов игрока Р2 |
ë û |
|
|
|
éé |
1 |
ù é |
2 |
ù é |
3 ù é |
4 ùù |
Þ |
|
|
é |
* ù |
é |
é |
|
2 |
ù é |
|
4 |
ù |
ù |
|
|
|
|
[A] = ëëa |
|
û;ëa |
|
û; ëa |
û;ëa |
ûû |
|
|
ëA |
û |
= ë |
ëa |
|
û;ëa |
|
û |
û. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
éé |
* |
ùù |
||
Представим эквивалентную матрицу éA* ù построчно |
éA* ù |
= |
ê |
ëa1 |
û |
ú . |
||||||||||||||||||
éa* |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
ë |
û |
|
|
|
|
ë |
û |
|
|
ê |
ùú |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
ë |
2 |
ûû |
|
С учётом конкретных данных имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
éA* ù = |
é |
-3 -1 |
Þ |
éa1* |
ù |
= [-3;-1] |
|
. |
|
|
|
|
|
|
|
|
||||||||
2 |
ù |
ë û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ë |
û |
|
ê |
-5ú |
|
é |
* |
ù |
= [ 2;-5] |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
ë |
|
û |
|
ëa2 |
û |
|
|
|
|
|
|
|
|
|
|
|||||
64
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
Дальнейшее решение с использованием эквивалентной матрицы éA* ù
ë û
можно представить как
|
|
|
|
|
|
|
v = max min[x ; x |
]´ éA* ù ´ é y1* ù, |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
y |
1 |
2 |
|
|
ë |
û |
ê |
|
* |
ú |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë y2 |
û |
|
|
|||
где в нашем конкретном случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y* = y |
2 |
; |
y* = y |
4 |
и поскольку |
y |
2 |
= 1- y , |
|
то |
y* |
= 1- y* . |
|||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
||||||
Перейдём к скаляризации промежуточного этапа решения |
|
||||||||||||||||||||||||
|
|
* |
|
* |
|
|
é * |
ù |
é |
y1* ù |
|
* |
|
|
* |
|
é |
|
* |
ù |
é |
y1* ù |
|||
|
g1 ( y1 ) = |
ëa1 |
û |
´ ê |
* ú; |
|
g2 |
( y1 ) = |
ëa2 û |
´ ê |
|
* ú. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
ë1 |
- y1 |
û |
|
|
|
|
|
|
|
|
|
|
ë1 |
- y1 û |
|
Вернувшись к исходной нумерации стратегий, получим частные |
|||||||||||||||||||||||||
платёжные функции игрока Р2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
g2 ( y2 ) = |
é * |
ù |
é |
y2 |
ù |
|
g4 ( y4 ) = |
é |
|
* |
ù |
é |
y4 |
ù |
|||||||||||
ëa1 |
û |
´ ê |
|
ú; |
|
ëa |
2 |
û |
´ ê |
|
ú . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
ë1 |
- y2 û |
|
|
|
|
|
|
|
|
|
|
ë1- y4 û |
|||
Подставляя конкретные данные, получим |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
g2 ( y2 ) = [-3;-1]´ |
é |
y2 |
ù |
|
é |
|
|
|
|
|
ù |
|
|
|||||||||
|
|
|
ê |
|
ú |
= ë-2 |
× y2 -1û; |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ë1 |
- y2 û |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
g |
|
( y |
|
) = |
[ 2; - |
5]´ |
é |
y2 |
ù |
|
= é |
7 × y |
|
|
- 5ù. |
|
|
|||||
|
|
|
4 |
2 |
ê |
|
ú |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
û |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ë1 |
- y2 û |
|
|
|
|
|
|
|
|
|
|
||
Построив |
графики |
|
платёжных |
функций |
g2 ( y2 ), |
g4 ( y4 ), как это |
|||||||||||||||||||
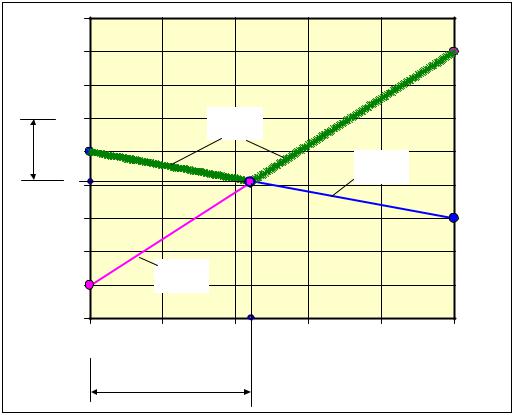
показано на рис. 8.2, перейдём к построению кусочно-линейной зависимости
для максимальных значений в вертикальных сечениях
ξ( y2 ) = max{g2 ( y2 ); g4 ( y2 )}.
65
Т Е О Р И Я |
И Г Р |
|
|
|
|
В.М.Дуплякин |
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
ν |
0 |
|
ξ( y2 ) |
|
|
|
|
-1 |
|
|
|
g2 (y2 ) |
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
-4 |
g4 (y2 ) |
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
y2 |
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
|
y2(0) |
|
|
|
|
|
|
Рис. 8.2 – Оптимизация смешанных стратегий игрока Р2 |
|
|||||
Приравняв уравнения линий g2 ( y 2 ) и g4 ( y 4 ) , найдём оптимальное относительное содержание второй стратегии игрока Р2
g2 ( y2(0) ) = g4 ( y2(0) ).
Используя найденные ранее зависимости для платёжных функций,
запишем следующее
-2× y2(0) -1 = 7 × y2(0) - 5.
Отсюда найдём оптимальное содержание второй стратегии в смеси стратегий второго игрока
y2(0) = 94 = 0,44(4).
Очевидно, что оптимальное содержание четвёртой стратегии в смеси стратегий игрока Р2 определяется как
y4(0) = 1- y2(0) = 95 = 0,55(5).
Учитывая наличие "пустых" стратегий игрока Р2, матрицу-столбец
выбора оптимальных смешанных стратегий для второго игрока запишем в виде
é |
(0) ù |
T |
|
= [ 0; 0,44(4); 0; 0,55(5) ] . |
|||
ë y |
û |
66
Т Е О Р И Я И Г Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В.М.Дуплякин |
|||
|
Примечание. Зная цену оптимальной игры из решения для первого игрока |
|||||||||||||||||
ν = - |
17 , можно |
найти |
y2(0) из |
уравнения |
одной |
из |
частных |
платёжных |
||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функций, например, как |
- 17 = - × |
|
|
|
|
|
|
4 |
|
|
|
|
||||||
|
ν = |
g2 ( y |
(0) |
|
Þ |
(0) |
- |
1 |
Þ |
y |
(0) = |
= |
0,44(4) |
. |
||||
|
|
2 ) |
|
9 |
2 |
y 2 |
|
|
2 |
9 |
|
|
||||||
Этот вариант решения рекомендуется использовать в качестве проверки.
Дополнительный анализ игры в чистых стратегиях
Если игра производится только один раз, то она реализуется в так называемых чистых стратегиях, поскольку каждый из игроков может выбрать одну из доступных ему стратегий.
При многократном повторении игры игроки могут придерживаться однажды выбранных стратегий, и это им выгодно, если нижняя цена игры совпадает с верхней ценой, что собственно и является решением в чистых стратегиях, отступать от этих стратегий невыгодно ни одному из игроков.
Если же нижняя цена игры ниже верхней, то оптимальный результат
достигается только при достаточно большом повторении игры со случайным выбором стратегий при их перемешивании в заданной пропорции, это и есть решение в смешанных стратегиях.
В рассматриваемом примере с заданной платёжной матрицей игры 2 × 4 оптимальное решение в смешанных стратегиях реализуется при следующих частотах (вероятностях) выбора стратегий:
Игрок Р1: éx(0) |
ù = [0,77(7); 0,22(2)]. |
|
||
|
ë |
û |
= [ 0; 0,44(4); 0; 0,55(5) |
]T . |
Игрок Р2: |
é y(0) ù |
|||
|
ë |
û |
|
|
При достаточном повторении игры с заданным оптимальным перемешиванием средний выигрыш игрока Р1 составит νopt P1 = −1,88(8) , т.е.
первый игрок поигрывает и его цель - минимизировать снизить возможный средний проигрыш.
Очевидно, что игрок Р2 в данной игре при оптимальном смешивании стратегий добивается максимизации своего среднего выигрыша, который составляет νopt P2 = −νopt P1 = 1,88(8).
Сопоставим результаты оптимизации рассматриваемой игры в смешанных стратегиях с теми результатами, которые можно получить в чистых стратегиях.
67
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
1. Максимально возможный результат игрока Р1 при наиболее благоприятном поведении игрока Р2, как видно из представленной платёжной
матрицы формируется следующим образом
|
[x] = [1; 0], |
[ y] = [0; 0; 1; 0]T |
Þ |
νmax P1 = a1,3 |
= 4 . |
2. |
Наихудший результат Р1 |
|
|
|
|
|
[x] = [0; 1], |
[ y] = [0; 0; 0; 1]T |
Þ |
νmin P1 = a2,4 = -5. |
|
3. Максимально возможный результат Р2 |
|
|
|||
|
[x] = [0; 1], |
[ y] = [0; 0; 0; 1]T |
Þ |
νmax P2 = -a2,4 = 5. |
|
4. |
Наихудший из возможных результатов игрока Р2 |
|
|||
|
[x] = [1; 0], |
[ y] = [0; 0; 1; 0]T |
Þ |
νmin P2 = -a1,3 |
= -4. |
Как видно из приведенных результатов для одноходовой игры, переход к
оптимальному смешиванию стратегий при её многократном повторении позволяет первому игроку значительно снизить проигрыш по сравнению с максимальным возможным для него проигрышем, а второй игрок гарантирует себе выигрыш.
8.2.Игры m × 2
Вматричных играх m × 2 , платёжная матрица имеет следующий вид
é a |
a |
ù |
ê 1,1 |
1,2 |
ú |
[A] = êa2,1 |
a2,2 |
ú . |
ê ... |
... |
ú |
êa |
a |
ú |
ë m,1 |
m,2 |
û |
Решить такую задачу можно чисто технически, сведя её к уже рассмотренной задаче 2 × n , выполнив транспонирование платёжной матрицы, положив n = m и перенумеровав игроков.
Рассмотрим прямо решение без транспонирования, основываясь на рассмотренной методике решения задачи 2 × n .
68
Т Е О Р И Я И Г Р |
В.М.Дуплякин |
||
Сначала вычисляются частные платёжные функции игрока Р2 для смеси |
|||
é y |
1 |
ù |
при условии, что игрок Р1 применяет чистую стратегию [ai ] |
стратегий ê |
ú |
||
ë y 2 |
û |
|
|
gi ( y) = [ai ]´[y] |
é y |
|
ù |
é |
y |
|
ù |
при i = 1, 2, 3, 4, где [y] = ê |
1 |
ú |
= ê |
|
1 |
ú . |
|
|
ë y 2 |
û |
ë1 |
- y1 û |
|||
Далее строится кусочно-линейная функция максимального выигрыша
второго игрока
ζ ( y1) = max{g1( y1); g2 ( y1 ); g3 ( y1); g4 ( y1)}.
Цена игры определяется как ν= minζ ( y1).
y1
Далее зная цену игры, получим оптимальное содержание первой стратегии в смеси стратегий второго игрока, подставив значение цены и одно из уравнений тех частных платёжных функций, пересечение которых даёт найденный оптимум.
В качестве примера рассмотрим игру 4 × 2 с платёжной матрицей,
имеющей следующий вид
é2 |
6ù |
ê |
ú |
[A] = ê5 |
1ú. |
ê3 |
9ú |
ê |
ú |
ë7 |
4û |
Пропуская конкретные вычисления, обратимся к графическому представлению выполненного решения, представленному на рис. 8.3, которое
привело к следующим результатам
ν = 5,680; y1(0) = 0,560; y2(0) = 0,440 .
69
