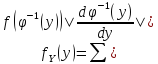- •Произведением
- •16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.
- •19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.
- •38 Дискретный случайный вектор
- •Условие независимости для дискретной случайной вел-ны:
- •Условие независимости для непрерывной случайной велечины:
- •Сходимость последовательностей случайных величин
- •49. Закон больших чисел
- •55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.()
- •Квантили распред-я
- •17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
- •Интеграл Эйлера:
- •Свойства:
- •46 Рассмотрим двумерный случайный вектор (X,y), законы распределения координат которого известны
Интеграл Эйлера:
Интеграл
Эйлера сходится т.к. при х>1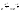 ,
найдем интеграл
,
найдем интеграл
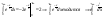 -сходится
по 1му признаку сравнения
-сходится
по 1му признаку сравнения
Проверим
условия нормировки: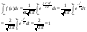
Найдем
числовые характеристики: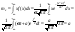
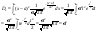 ;
;
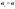
Смысл параметров распределения состоит в том, что они являются соответственно мат. ожиданием и дисперсией нормального распределения.
36. Влияние параметров распределения. Влияние параметров а и σ на вид кривой плотности. Если σ=const, то при изменении параметра а график ф-ииf(x) не изменяя своей формы сдвигается влево или вправо по оси ОХ.Если а=const, то изменение σ равносильно изменению масштаба по осям. При увеличении σ, кривая плотности прижимается к оси ОХ. При уменьшении σ кривая плотности вытягивается вверх, одновременно сжимаясь с боков, однако площадь под кривой распределения все равно остается равной 1.
Если
а=0, а σ=1 нормальный закон называется
стандартным. Для него ф-ия плотности
имеет вид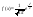 ф-ия
Гаусса.
ф-ия
Гаусса.
Ф-ия
распределения для случайной величины
Х, распределенной по стандартному
закону имеет вид: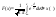 -ф-ия
Лапласа.
Этот интеграл не выражается через
элементарные ф-ии. Его значение находят
по таблице.
-ф-ия
Лапласа.
Этот интеграл не выражается через
элементарные ф-ии. Его значение находят
по таблице.
Вероятность
попадания
нормальной случайной величины Х на
заданный интервал , определяется
следующим образом: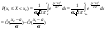
Вероятность
попадания в симметричный интервал.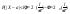
37.
Опред:
совокупностью
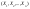 случ
величин, значения которых совместно
описывают некоторые случайные явл-я
наз-тся случайным вектором или многомерной
случайной величиной. Случ величины
случ
величин, значения которых совместно
описывают некоторые случайные явл-я
наз-тся случайным вектором или многомерной
случайной величиной. Случ величины
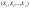 наз-ся компонентам, составляющими или
коорд-ми случ вектора.
наз-ся компонентам, составляющими или
коорд-ми случ вектора.
Ф-ей распределения
случ вектора (XY)
наз-ют вер-сть совместного выполнения
2х неравенств X<x;Y<y.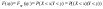 Геометрически
ф-ия распределения F(XY)
есть вероятность попадания случайной
точки в бесконечный квадрат с вершиной
в т.(xy).
Геометрически
ф-ия распределения F(XY)
есть вероятность попадания случайной
точки в бесконечный квадрат с вершиной
в т.(xy).
Свойства:
1)
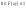 из
определения как вероятность.
из
определения как вероятность.
2)
Ф-ия распределения не убывает по обоим
аргументам.
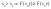 ;
;
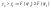
3) непрерывна
слева по обоим аргументам.
непрерывна
слева по обоим аргументам.
4)
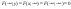
5)
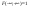
6)
свойство согласованности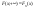 ;
;
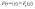
Таким
образом зная совместную ф-ию распред-я
случ вектора можно найти ф-ии распределения
отдельных координат случ вектора.
Обратное, без доп информации, не верно.7)
Вероятность попадания в прямоугольник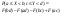
45. M(X,Y) сл.связь
1)Независимы
2)Функционизированны Y=φ(X)
3)Зависимы в вероятностном смысле (стохастически зависимы, например рост и вес человека) – прямой функциональной зависимости нет, но некоторая зависимость все же присутствует. Если Х – рост, Y – вес, то Y(кг)=X(см)-100 с определенной степенью точности.
Рассмотрим случай функциональной зависимости: если Х – случайная величина, φ(Х) – неслучайная функция, то Y=φ(Х) – случайная величина, ???(хз какое слово) распределения.
Т.8.1.:
пусть ф-ция y=φ(х)
является строго монотонной, дифференцируемой
для любых действующих х, тогда плотность
случайной величины Y=φ(Х)
определяется формулой
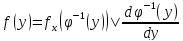
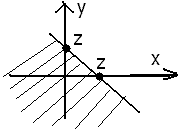
Доказательство: пусть φ(х) строго возрастает, тогда
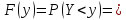
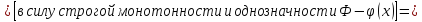
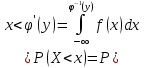

Пусть y=φ(x) – строго убывает, тогда производная от φ-1(y) будет <0, но в формуле стоит модуль, значит этот случай оценивается аналогично. Ч.т.д.
Если функция y=φ(x) не монотонная в области значений случайной величины Х, то ее область определения разбивают на участки монотонности и получают формулу