
- •Произведением
- •16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.
- •19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.
- •38 Дискретный случайный вектор
- •Условие независимости для дискретной случайной вел-ны:
- •Условие независимости для непрерывной случайной велечины:
- •Сходимость последовательностей случайных величин
- •49. Закон больших чисел
- •55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.()
- •Квантили распред-я
- •17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
- •Интеграл Эйлера:
- •Свойства:
- •46 Рассмотрим двумерный случайный вектор (X,y), законы распределения координат которого известны
17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
Пусть прост-во элемент событий – ограниченная область в n-мерном прост-ве. Назовём мерой области её длину, если n=1; площадь, если n=2; и объём, если n=3.
Рассмотрим
случайный эксперимент, состоящий в
броске точки в область ,
число исходов несчётно. Будем считать,
что исходы равномерно распределены в
области
,
число исходов несчётно. Будем считать,
что исходы равномерно распределены в
области
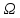 ,
т.е. вер-ти попадания точки в произвольное
подмножество
,
т.е. вер-ти попадания точки в произвольное
подмножество
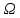 пропорциональны объёму объёму этого
подмножества. Это говорит о равновозможности
исходов. Рассм. событие A
пропорциональны объёму объёму этого
подмножества. Это говорит о равновозможности
исходов. Рассм. событие A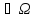 ; мера:
; мера:
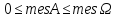
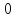 Определение:
геометрической вер-тью события А
называется величина: P(A)=
Определение:
геометрической вер-тью события А
называется величина: P(A)=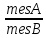
Статистическое: в большом классе событий вер-ть нельзя вычислить или с помощью классического определения вер-ти или с пом. геометрического определения вер-ти, т.к. исходы в них не равновозможны. Для таких событий, обладающих св-вом устойчивости частот и св-вом массовости, применимо статистическое определение вер-ти. Определение: за вер-ть события А в статистическом смысле принимается относительная частота события А в достаточно большом числе опытов n:
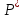 (A)=
(A)=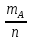 ,
n
– число опытов,
,
n
– число опытов,
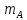 -частота
появления события А. Плюсы определения:
оно универсально, применимо к любым
случайным экспериментам. Минусы: 1)
требует большого числа опытов,2) Лишь
примерно равно точной вероятности,
т.к. в другой серии из n
опытов вер-ть
-частота
появления события А. Плюсы определения:
оно универсально, применимо к любым
случайным экспериментам. Минусы: 1)
требует большого числа опытов,2) Лишь
примерно равно точной вероятности,
т.к. в другой серии из n
опытов вер-ть
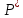 (A)
может
быть совсем другой.
(A)
может
быть совсем другой.
34.
Равномер распределение.
Говорят, что если непрер случ величина
Х имеет на отрезке [a,b]
равномер распред если на этом отрезке
ее ф-я плотности постоянна.
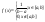 Записывается
как:
Записывается
как: Проверим усл нормировки:
Проверим усл нормировки: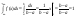
Условия нормировки выполняются:
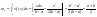 ;
;
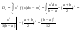 ;
;
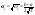 Проверим
с какой вероятностью будет выполняться
правило сигм:
Проверим
с какой вероятностью будет выполняться
правило сигм: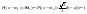
Показат
распред. Говорят,
что непрер случ вел-на имеет показат
распреде, если множество ее значений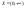 ,
и плотность вер-тей определяется
формулой:
,
и плотность вер-тей определяется
формулой: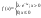 Где
Где
 –параметр
распред-я.Усл нормировки:
–параметр
распред-я.Усл нормировки: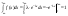
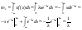 ;
;
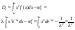 ;
;
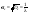 Проверим,
с какой вероятностью будет выполняться
правило сигм:
Проверим,
с какой вероятностью будет выполняться
правило сигм: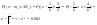 Распред
Коши. Непрер
случ вел-на распред-на по закону Коши,
если множество ее значений
Распред
Коши. Непрер
случ вел-на распред-на по закону Коши,
если множество ее значений , а плотность вер-ти имеет вид:
, а плотность вер-ти имеет вид: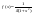 ,
,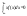 -этот
интеграл не сх-ся абсолютно
-этот
интеграл не сх-ся абсолютно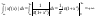 Замечание:
можно было предположить, что
Замечание:
можно было предположить, что , т.к. подынтегральная ф-ия нечетная, но
это правило верно только для абсолютно
сходящихся интегралов, поэтому для
распределения Коши НЕ СУЩЕСТВУЕТ мат.
Ожидания и дисперсии.
, т.к. подынтегральная ф-ия нечетная, но
это правило верно только для абсолютно
сходящихся интегралов, поэтому для
распределения Коши НЕ СУЩЕСТВУЕТ мат.
Ожидания и дисперсии.
35.
Определение:
Говорят, что
непрерывная случайная величина Х имеет
нормальное распределение с параметрами
, если множество ее значений -вся числовая
прямая, а плотность вероятности имеет
вид: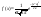
Мода
нормально распределенной величины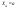

Кривая плотности нормального распределения имеет симметричный вид и называется кривой Гаусса. Чтобы проверить условие нормировки докажем лемму:
