- •Произведением
- •16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.
- •19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.
- •38 Дискретный случайный вектор
- •Условие независимости для дискретной случайной вел-ны:
- •Условие независимости для непрерывной случайной велечины:
- •Сходимость последовательностей случайных величин
- •49. Закон больших чисел
- •55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.()
- •Квантили распред-я
- •17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
- •Интеграл Эйлера:
- •Свойства:
- •46 Рассмотрим двумерный случайный вектор (X,y), законы распределения координат которого известны
55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.()
В
этом случае рассмат-ся стат-ка
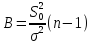 ,
имеющ-я расп-ие
,
имеющ-я расп-ие
 с
k=n-1
степ-ми своб-ы, где n-объем
выборки. Бум искать довер-ую обл-ть в
виде:
с
k=n-1
степ-ми своб-ы, где n-объем
выборки. Бум искать довер-ую обл-ть в
виде:
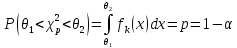
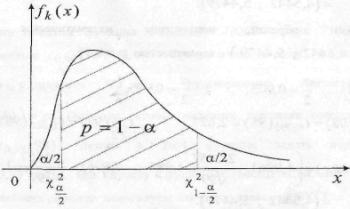
Квантили распред-я
Как и в предыд-ем случае, бум считать площади под «хвостами»
кривой
расп-ия равными по
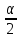 каждая. Тогда
гран-ы интер-а совпадут с квантилями:
каждая. Тогда
гран-ы интер-а совпадут с квантилями:
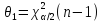 ,
,
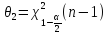 .
Таким обр-м получ-м
.
Таким обр-м получ-м
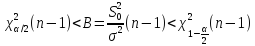 .
Подст-в в получ-ое нерав-во знач-я
.
Подст-в в получ-ое нерав-во знач-я
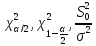 ,
n
и решив нерав-во относ-но
,
n
и решив нерав-во относ-но
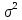 получим довер-ый
интервал для неизв-ой дисп-ии
получим довер-ый
интервал для неизв-ой дисп-ии
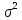 норм-о распред-ой
случ-ой велич-ы X
с неизв-ым
мат-им ожид-ем и заданным уровнем
значимости
норм-о распред-ой
случ-ой велич-ы X
с неизв-ым
мат-им ожид-ем и заданным уровнем
значимости
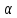 :
:
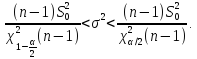 Следует
отметить, что если мат-ое ожидание
генер-ой
Следует
отметить, что если мат-ое ожидание
генер-ой
совок-ти известно, то довер-ый интервал для дисп-ии будет иметь
другой вид.
Длина довер-го интер-а характ-ет точность оцен-ия и
зависит от объема
выб-и n
и довер-ой
вер-ти
 .
Чем < длина
довер-го интер-а, тем надежнее оценка.
При увелич-и объема выборки длина
довер-го интер-а уменьшается.
.
Чем < длина
довер-го интер-а, тем надежнее оценка.
При увелич-и объема выборки длина
довер-го интер-а уменьшается.
56)
1.Статист-ая гипотеза. 2.Ошибки I
и II
рода. 3.Критерий согласия
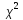 Пирсона
Пирсона
1Статист-ой гипотезой назыв-т любое утверж-е о виде или о парам-х распр-ия генер-ой совок-ти. Например, статист-ми явл гипотезы:
1. генер-ая совок-ть распред-на по норм-му зак-у или
люб другому конкретно зад-му зак-у (гипотеза о виде распр-ия);
2.
если изв-о, что ген-ая совок-ть распр-на
по
норм-му
закону, то парам-ы норм-го закона равны
выб-ым
характ-ам:
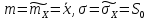 (параметрическая
гипотеза).
(параметрическая
гипотеза).
Гипотезу о виде распр-ия выдвигают на основе схожести
гистограммы или полигона частот с соответ-ей кривой одного из
теор-их зак-в (норм-го, равно-го, Пуассона и т. п.).
Когда
предпол-ие о виде распр-ия ген-ой
совокупности принято, следует проверить
гипотезу о параметрах этого распр-ия.
2.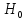 -нулевая
гипотеза. Альтер-ми
назыв гипотезы,
которые противоречат нулевой. Если
отвергается
-нулевая
гипотеза. Альтер-ми
назыв гипотезы,
которые противоречат нулевой. Если
отвергается
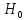 ,
то прин-ся одна из альтер-ых гипотез.
При пров-е статист-х гипотез могут быть
допущены ошибки 2-х родов с вер-ми:
,
то прин-ся одна из альтер-ых гипотез.
При пров-е статист-х гипотез могут быть
допущены ошибки 2-х родов с вер-ми:
1.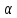 -вер-ть
отклонить гипотезу
-вер-ть
отклонить гипотезу
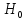 ,
при условии, что она верна
,
при условии, что она верна
(ошибка I рода);
2.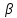 -верть
принять гипотезу
-верть
принять гипотезу
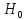 ,
при условии, что она неверна
,
при условии, что она неверна
(ошибка II рода).
Напр-р,
в радиолок-и -вер-ть
проп-а сигнала,
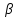 -вер-ть
ложной тревоги.
-вер-ть
ложной тревоги.
Ясно, что чем меньше
будут ошибки I
и II
рода, тем точнее статист-ий вывод. Однако
при зад-ом объеме выборке одновр-но
умен-ть
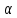 и
и
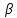 невозм-о. Единст-ый способ одноврем-го
умен-ия
невозм-о. Единст-ый способ одноврем-го
умен-ия
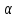 и
и
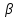 сост в увелич-и объема выборки.
сост в увелич-и объема выборки.
56)
3.Схема
прим-ия крит-я согл-я
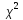 :
:
1)
Выдв-ся гипотеза
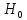 :
ген-ая совок-ть имеет норм-ое распр-ие
с плот-ю вер-ей
:
ген-ая совок-ть имеет норм-ое распр-ие
с плот-ю вер-ей
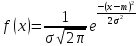 с парам-и
с парам-и
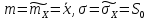 , т.е. выб-ое сред-е
, т.е. выб-ое сред-е
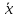 и модиф-ая выб-ая дисп-я
и модиф-ая выб-ая дисп-я
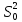 прин-ся соотв-но за мат-ое
ожид-е m
и
дисп-ию
прин-ся соотв-но за мат-ое
ожид-е m
и
дисп-ию
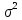 норм-но
распр-ой случ-й велич.
2)
По выб-е наблюд-ий случ-й велич-ы X
сост-ся
групп-ый вариац-ый ряд. 3) Выч-ся вер-ти
норм-но
распр-ой случ-й велич.
2)
По выб-е наблюд-ий случ-й велич-ы X
сост-ся
групп-ый вариац-ый ряд. 3) Выч-ся вер-ти
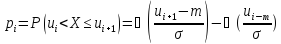 .
Здесь
.
Здесь
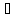 (x)
– фу-ия
расп-ия норм-го зак-а N(0;1),
значе-я которой нах-т по табл-м.
4)
Выч-ся выб-ое знач-е статистики критерия
(x)
– фу-ия
расп-ия норм-го зак-а N(0;1),
значе-я которой нах-т по табл-м.
4)
Выч-ся выб-ое знач-е статистики критерия
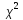 :
:
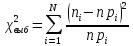 ,
где
N–число
интерв-ов разб-ия выб-и; n–объем
выб-и;
,
где
N–число
интерв-ов разб-ия выб-и; n–объем
выб-и;
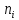 -частота
i-того
интервала;
-частота
i-того
интервала;
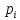 -
теор-ая
вер-ть попад-ия знач-й cлуч-й
велич-ы X
в
i-тый
интервал. К.Пирсон доказал, что эта
стат-а независ-о от вида распр-ия ген-ой
совокуп-ти при
-
теор-ая
вер-ть попад-ия знач-й cлуч-й
велич-ы X
в
i-тый
интервал. К.Пирсон доказал, что эта
стат-а независ-о от вида распр-ия ген-ой
совокуп-ти при
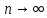 имеет
имеет
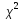 -
распр-ие с
-
распр-ие с
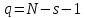 степ-и
своб-ы, где N–число
интер-в разб-я, s–число
оцен-х парам-в гипотетического зак-а
распр-ия. Для норма-го законаs=2(парам-ы
m
и
степ-и
своб-ы, где N–число
интер-в разб-я, s–число
оцен-х парам-в гипотетического зак-а
распр-ия. Для норма-го законаs=2(парам-ы
m
и
 ).
5).
Обл-ю отклон-я G(крит-й
обл-ю) гип-ы
).
5).
Обл-ю отклон-я G(крит-й
обл-ю) гип-ы
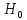 назыв-cя
такая обл-ь, при попадании в кот-ю
статистики
назыв-cя
такая обл-ь, при попадании в кот-ю
статистики
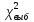 гип-а
гип-а
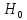 отклон-ся.
Обл-ь отклон-я G
выб-ся
так, чтобы вер-ть попад-я в нее велич-ы
отклон-ся.
Обл-ь отклон-я G
выб-ся
так, чтобы вер-ть попад-я в нее велич-ы
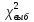 ,
когда гипотеза
,
когда гипотеза
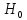 верна,
была равна уровню знач-ти
верна,
была равна уровню знач-ти
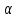 .
Тогда кри-ая точка
.
Тогда кри-ая точка
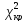 ,
огранич-ая обл-ь G,
опред-ся из ур-ия:
,
огранич-ая обл-ь G,
опред-ся из ур-ия:
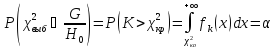 .
Из
этой ф-лы след-т, что крит-я точка
.
Из
этой ф-лы след-т, что крит-я точка
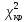 равна с квантили
равна с квантили
Распр-ия
Пирсона
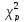 ,
отвеч-ей вер-ти
,
отвеч-ей вер-ти
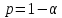 с
числом cтеп-й
своб-ы
с
числом cтеп-й
своб-ы
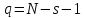 .
Таким
образом, если вычис-ая выб-ая стат-а
.
Таким
образом, если вычис-ая выб-ая стат-а
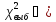 ,
то гипотеза
,
то гипотеза
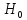 прин-ся.
Если
прин-ся.
Если
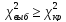 то
гип-а
то
гип-а
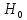 отвер-ся.
отвер-ся.
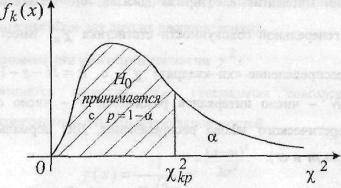
Выбор обл-и прин-ия гипотезы можно объяснить след-им
образом:
знач-я теор-х вер-й
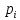 и
относит-ых частот
и
относит-ых частот
интер-в
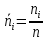 должны
быть =>
должны
быть =>
=>доста-о
близки, поэтому разн-и
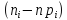 не
должны быть слишком велики. Стат-ий
вывод неверно форм-ть в виде: ген-я
не
должны быть слишком велики. Стат-ий
вывод неверно форм-ть в виде: ген-я
совок-ть имеет норм-ый зак распр-ия. Можно лишь
утв-ть, что данная выборка согл-ся с гипо-ой о норм-м
распр-ии
ген-ой совок-ти с парам-и
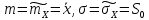 на
уровне значимости
на
уровне значимости