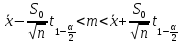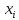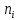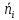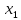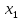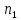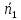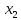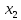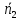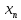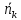- •Произведением
- •16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.
- •19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.
- •38 Дискретный случайный вектор
- •Условие независимости для дискретной случайной вел-ны:
- •Условие независимости для непрерывной случайной велечины:
- •Сходимость последовательностей случайных величин
- •49. Закон больших чисел
- •55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.()
- •Квантили распред-я
- •17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
- •Интеграл Эйлера:
- •Свойства:
- •46 Рассмотрим двумерный случайный вектор (X,y), законы распределения координат которого известны
Сходимость последовательностей случайных величин
Рассмотри плотность случайных величин (xn).чин
Опр. Если M[(xn-x)2]→0 при n→∞, то говорят, что плотность величин (xn). Сходится к х в среднеквадратичном смысле. При этом х м.б. как случайной, так и нет.
Опр.
Если для
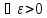 при n→∞
при n→∞
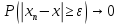 или
или
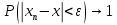 ,
то говорят, что последовательность
случайных величин (xn)→
к хпо вер-ти.
,
то говорят, что последовательность
случайных величин (xn)→
к хпо вер-ти.
Из неравенства Чебышева следует, что из сх-ти в среднеквадратичном смысле вытекает сх-ть по вер-ти.
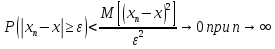
Обратное неверно.
49. Закон больших чисел
Теорема Чебышева.
Последовательность
(xn)
– последовательность попарнонезависимых
х одинаковораспределенных случайных
величин, имеющих конечные мат.ожидания
и дисперсию M[xn]=m,
D[xk]=δ2
тогда при n→∞
среднее арифметическое этих случайных
величин
 сх-ся вер-ти к m,
т.е.
сх-ся вер-ти к m,
т.е.
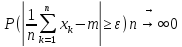
Док-во:
Пусть
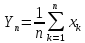

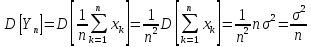
Решение
нер-ва Чебышева
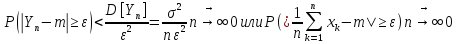
Эта
теорема служит обоснованием правила
среднего арифметического в теории
измерений, в соответствии с которой за
приближ.значение измерен.величины
следует брать среднее арифметическое
измерений, полученная при этом погрешность
равна
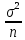 ,
что в n
раз выше, чем при измерении одной
величины.
,
что в n
раз выше, чем при измерении одной
величины.
Теорема
Бернулли. Относительная частота
появлений соб.А при n
независимых испытаний в схеме Бернулли
сос-ся при n→∞
по вер-ти к вер-ти появления соб.А в
одном испытании, т.е.
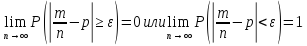
M – число появлений соб.А в n испытаниях.
Док-во:
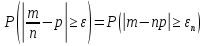
В
схеме испытаний Бернулли mx=np,
а Dx=npq,
тогда применяют к послед.выражению
нер-ва Чебышева, заменяя в нем x
на m,
а
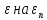 ,
получаем
,
получаем
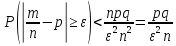 и при n→∞
получаем утверждение теоремы. Ч.т.д..
и при n→∞
получаем утверждение теоремы. Ч.т.д..
Теорема Бернулли является обоснованием статистического определения вероятности.
50) 1.Центр.пред.теор. 2. Локал и интегр теор Муавра-Лапласа.
1.Пусть(Xn)-
послед-ть независ и одинак распред случ
велич для нек M[Xn]=m,
D[Xn]=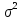 ,
,![]() n
тогда зак распред-я вероят случ велич
Xn
=
n
тогда зак распред-я вероят случ велич
Xn
=
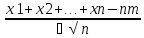 =
=
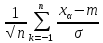 при n→∞,
стремится к норм закону N(0,1)
т.е.
при n→∞,
стремится к норм закону N(0,1)
т.е.
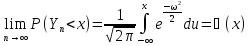 равномерна для
равномерна для
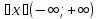 Замеч: Смысл ЦПТ можно счит, что сумма
Замеч: Смысл ЦПТ можно счит, что сумма
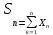 независ одинак распред случ величин
при достат-но больших N(практ-ки
при N≥30)
имеет закон норм распред-я с парам-ми
n,
m
и
независ одинак распред случ величин
при достат-но больших N(практ-ки
при N≥30)
имеет закон норм распред-я с парам-ми
n,
m
и
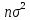
2.1
Лок-я теор:
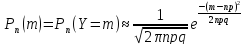 где p-вер-ть
появл соб-я А в одном испыт-ии, q-вер-ть
соб-я
где p-вер-ть
появл соб-я А в одном испыт-ии, q-вер-ть
соб-я
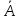 ,
,
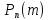 -вер-ть
того, что при n
незав-х испыт-й событие А появ-ся m
раз. Док-во:
-вер-ть
того, что при n
незав-х испыт-й событие А появ-ся m
раз. Док-во:
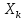 -число
появ-й соб-я А в K-том
испыт-ии. Тогда
-число
появ-й соб-я А в K-том
испыт-ии. Тогда
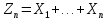 общ число появ-й соб-я А в n
испыт-х, т.к. испыт-я независ-ы, то и
случ-е велич-ы
общ число появ-й соб-я А в n
испыт-х, т.к. испыт-я независ-ы, то и
случ-е велич-ы
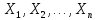 явл незав-ми. Тогда, согл ЦПТ случ-е
велич-ы
явл незав-ми. Тогда, согл ЦПТ случ-е
велич-ы
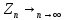 к норм-у зак-у, причём как известно
к норм-у зак-у, причём как известно
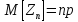 ,
,
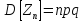 => при достат-о больших n
справ-а лок-я ф-ла Муавра-Лапласа
=> при достат-о больших n
справ-а лок-я ф-ла Муавра-Лапласа
2.2
Интегр теор:
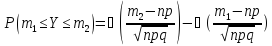 Док-во: Пусть
Док-во: Пусть
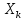 число появ-й соб-я А в одном испыт-ии,
тогда
число появ-й соб-я А в одном испыт-ии,
тогда
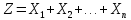 -число
появ-й соб-я А во всех n
испыт-х. Известно, что в одном испыт-ии
-число
появ-й соб-я А во всех n
испыт-х. Известно, что в одном испыт-ии
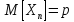 ,
,
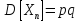 .
Подставляя эти знач в ф-лу ЦПТ получим
.
Подставляя эти знач в ф-лу ЦПТ получим
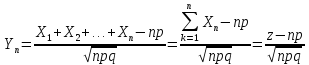 отсюда на основ-ии ф-лы из ЦПТ запишем,
что
отсюда на основ-ии ф-лы из ЦПТ запишем,
что
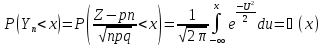 .
Тогда
.
Тогда
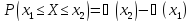 замен-я здесь
замен-я здесь
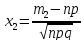 ,
,
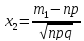 ,
получ-м утверд-е дан-й теоремы.
,
получ-м утверд-е дан-й теоремы.
51) 1.Стат-ие ряды. Их граф-е пред-е. 2.Выб-е сред-е, выб-я дисп-ия, модиф-ая выб-я дисп-ия.
1.
Стат-м
рядом
назыв
сов-ть пар
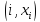 получ-х в рез-те эксп-nа.
Обычно стат-ие ряды оформ-ся в виде
таб-цы (табл.2), в 1-ом столбце которой
стоит индекс i(№
опыта), а во 2-ом - наблюденное знач случа
вел-ы
получ-х в рез-те эксп-nа.
Обычно стат-ие ряды оформ-ся в виде
таб-цы (табл.2), в 1-ом столбце которой
стоит индекс i(№
опыта), а во 2-ом - наблюденное знач случа
вел-ы
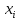 ,
кот назыв вариантой.
Если
одна и та же варианта встреч в выборке
нес-ко раз, то стат-ий ряд удобнее
запис-ть в виде табл.3.
,
кот назыв вариантой.
Если
одна и та же варианта встреч в выборке
нес-ко раз, то стат-ий ряд удобнее
запис-ть в виде табл.3.
Табл.2 Табл.3
|
Инд i |
Вар-та
|
Инд i |
Вар-та
|
Част
|
Относ. Част
|
|
1 |
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
… |
… |
… |
… |
… |
… |
|
n |
|
k |
|
|
|
Част
 (i=
(i=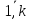 )
вар-ы
)
вар-ы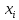 наз-ся
число повт-й варианты
наз-ся
число повт-й варианты
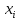 в
выб-е, прич
в
выб-е, прич
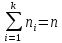 .
Относ-ой
част-й или
весом
.
Относ-ой
част-й или
весом
 (i=
(i=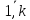 )
вар-ы
)
вар-ы наз-я
отнош-е част-ы вар-ы
наз-я
отнош-е част-ы вар-ы
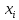 к
объему выборки n,
то ест
к
объему выборки n,
то ест ,
причем
,
причем
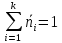
2.1Выб-ым
средним наз-ся
среднее арифм-ое элементов выб-и
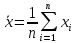 .
Согл зак больш чисел при увел-ии объема
выб-и сред ариф-ое сход-я по вер-ти к
мат-му ожид-ю генер-й совок-ти, то есть
.
Согл зак больш чисел при увел-ии объема
выб-и сред ариф-ое сход-я по вер-ти к
мат-му ожид-ю генер-й совок-ти, то есть
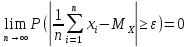 Таким обр-м, среднее ариф-ое может служ-ь
приб-м (оценкой) мат-го ожид-я
Таким обр-м, среднее ариф-ое может служ-ь
приб-м (оценкой) мат-го ожид-я
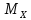 ген-ой
сов-ти.
ген-ой
сов-ти.
2.2
Выбор-ой
диспер-ей назыв-ся
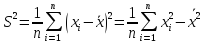
2.3Модиф-ой
выбор-ой диспер-ей назыв-ся
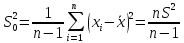 Все эти выбор-ые числ-е хар-ки завис от
выб-rи
и поэтому явл-cя
случ-ми велич-ми. Их знач-я лишь приближ-нно
равны соответ-щим числ-ым характ-ам
генер-ой совок-ти.
Все эти выбор-ые числ-е хар-ки завис от
выб-rи
и поэтому явл-cя
случ-ми велич-ми. Их знач-я лишь приближ-нно
равны соответ-щим числ-ым характ-ам
генер-ой совок-ти.
52) 1.Св-ва точ-ых оценок: несмещ-ть, сост-ть, эффект-ть. 2.Смещенная и несмещенная оценки дисперсии
1.
Точ-ой
оценкой
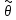 неизв-го
парам-а
неизв-го
парам-а
 распред-ия
случ-ой велич-ы X
назыв-ся
такая ф-ия от выб-ки (статистика)
распред-ия
случ-ой велич-ы X
назыв-ся
такая ф-ия от выб-ки (статистика)
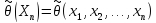 ,
знач-е кот-ой прин-ся за приб-ое знач-е
истинного парам-а,то ест
,
знач-е кот-ой прин-ся за приб-ое знач-е
истинного парам-а,то ест
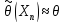
1.1Оценка
 парам-а
назыв-ся несмещ-ой,
если ее мат-ое ожид-е равно оцениваемому
парам-у
парам-а
назыв-ся несмещ-ой,
если ее мат-ое ожид-е равно оцениваемому
парам-у
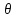 :
:
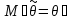 .
Известно, что
.
Известно, что
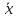 – несмещ-ая
оценка мат-го ожид-ия,
– несмещ-ая
оценка мат-го ожид-ия,
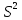 смещ-ая
оценка дисп-ии и
смещ-ая
оценка дисп-ии и
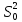 несмещ-ая
оценка дисп-ии 1.2Оценка
несмещ-ая
оценка дисп-ии 1.2Оценка
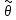 парам-а
назыв-ся сост-ой,
если она сх-я по вер-ти к точ-у знач-ю
оцен-го парам-а
парам-а
назыв-ся сост-ой,
если она сх-я по вер-ти к точ-у знач-ю
оцен-го парам-а
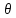 ,то
есть
,то
есть
 Сост-ой оц-кой
мат-го ожид-я явл-ся выб-ое среднее
Сост-ой оц-кой
мат-го ожид-я явл-ся выб-ое среднее
 а сост-ми оценками дисп-ии – выбор-ая
дисп-ия
а сост-ми оценками дисп-ии – выбор-ая
дисп-ия
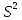 и модиф-ая выб-ая дисп-ия
и модиф-ая выб-ая дисп-ия
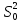 1.3Несмещ-ая
оценка
1.3Несмещ-ая
оценка
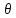 парам-а
назыв-ся эффек-ой,
если
она имеет min
дисп-ию среди всех несмещ-ых оценок
этого парам-а. Для норм-го зак-а распред-ия
эффек-ой оценкой мат-го ожид-ия
парам-а
назыв-ся эффек-ой,
если
она имеет min
дисп-ию среди всех несмещ-ых оценок
этого парам-а. Для норм-го зак-а распред-ия
эффек-ой оценкой мат-го ожид-ия
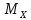 явл-ся среднее арифм-ое
явл-ся среднее арифм-ое
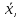 а эффек-ых оценок дисп-ии не сущ-ет.
Однако
а эффек-ых оценок дисп-ии не сущ-ет.
Однако
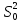 и
и
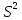 явл-ся
асимптотически эффек-ми оценками
дисп-ии
явл-ся
асимптотически эффек-ми оценками
дисп-ии
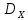 для этого закона.
для этого закона.
2Оценкой дисп-ии
случ-ой величины X
служат выб-ая
дисп-ия и модиф-ая выб-ая дисп-ия, вычис-ые
по фор-ам:
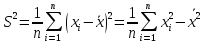
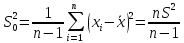 след-но,
след-но,
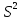 - явл-ся смещ-ой оценкой дисп-ии, а
- явл-ся смещ-ой оценкой дисп-ии, а
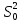 - несмещ-ой оценкой дип-ии
- несмещ-ой оценкой дип-ии
53)
Расп-ия
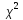 и Стьюдента
и Стьюдента
1.1
Пусть X1,
X 2
,…,
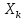 – норм-но
распред-ые независ-ыес
луч-ые
вел-ны, причем мат-ое ожид-ие каждой из
них равно 0, а среднеквадратическое
отклонение – 1, то есть
– норм-но
распред-ые независ-ыес
луч-ые
вел-ны, причем мат-ое ожид-ие каждой из
них равно 0, а среднеквадратическое
отклонение – 1, то есть
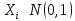 .
Тогда
сумма квадратов этих величин:
.
Тогда
сумма квадратов этих величин:
 распред-а по зак-у
распред-а по зак-у
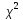 («хи
квадрат») с k
степ-ми своб-ы
(«хи
квадрат») с k
степ-ми своб-ы
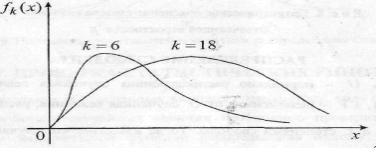
Рис.1
Графики
плот-ти вероят-ей распр-ия
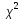
Плот-ть
вер-ей этого распр-ия имеет вид
 ,
,
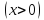 ,
где
,
где
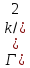 - гамма-фукция. График
плот-и вероят-ей
- гамма-фукция. График
плот-и вероят-ей
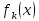 при
малых k имеет
длинный
при
малых k имеет
длинный
правый «хвост», а с ростом k стан-ся почти симмет-ым(Рис.1)
Квантили
расп-ия
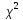 обозн-ся
обозн-ся
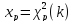 (Рис.2)
(Рис.2)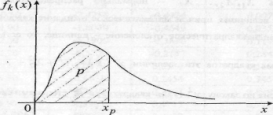
Рис.2
Геом-ое
опис смысла квантили
 отвеч-щей вероят p.
отвеч-щей вероят p.
1.2Пусть
U-норм-о
распред-ая случ велич-а, причём
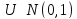 ,
a
V-независ-ая
от U
случ-ая велич-а, распред0ая по зак-у
,
a
V-независ-ая
от U
случ-ая велич-а, распред0ая по зак-у
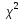 с
k
степ-ми своб-ы. тогда изв-но, что случ-ая
велич-а
с
k
степ-ми своб-ы. тогда изв-но, что случ-ая
велич-а
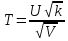 имеет t-распред-е
или распред-е Стьюдента с k
степ-ми своб-ы. Плот-ть вер-ей этого
распред-ия имеет вид:
имеет t-распред-е
или распред-е Стьюдента с k
степ-ми своб-ы. Плот-ть вер-ей этого
распред-ия имеет вид:
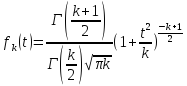
При
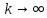 распр-ие Стью-а стрем-я к норм-у и при
распр-ие Стью-а стрем-я к норм-у и при
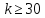 практ-и не отлич от норм-го N(0,1)
т.к. грай плот-и вер-ей распр-ия СТью-а
симмет-ен относ t=0,
то
практ-и не отлич от норм-го N(0,1)
т.к. грай плот-и вер-ей распр-ия СТью-а
симмет-ен относ t=0,
то
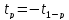 (Рис.3)
(Рис.3)
54) Довер-ый интер-л для мат-го ожид-ия при неизв-ой дисп-ии норм-о распред-ой ген-ой совокуп-ти.
Пусть случ-ая велич-а X имеет норм-ое распр-ие с
Парам-ми
m
и
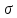 .
Найдем довер-ый интер-л для мат-го
ожид-ия m в
предположении, что дисп-ия
.
Найдем довер-ый интер-л для мат-го
ожид-ия m в
предположении, что дисп-ия
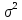 неизв-а
и задан уровень
неизв-а
и задан уровень
значимости
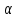 .
Англ-ий математик Госсет (псевдоним
Стьюдент) доказал, что стат-ка
.
Англ-ий математик Госсет (псевдоним
Стьюдент) доказал, что стат-ка
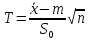 имеет распр-ие
Стьюдента с k
= n
−1
имеет распр-ие
Стьюдента с k
= n
−1
степ-ми
свободы. Так как кривая плот-ти вер-ей
распр-ия Стьюдента симм-на относ-но
t =
0, будем искать
довер-ую обл-ть в виде:
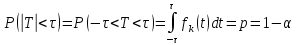
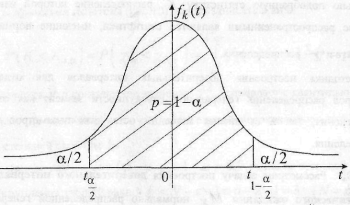
Из рис видно, что площадь под графиком каждого из
Симм-ых
«хвостов» будет равна
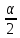 ,
тогда знач-я границ интер-а совпадут с
квантилями
,
тогда знач-я границ интер-а совпадут с
квантилями
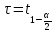 и
и
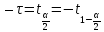 .
Таким обр-м получ-м
.
Таким обр-м получ-м
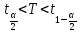 или
или
 .
Подст-в в
получ-ое нерав-во знач-я
.
Подст-в в
получ-ое нерав-во знач-я
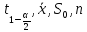 и разрешив это
нерав-во относ-но m,
получим довер-ый интервал
и разрешив это
нерав-во относ-но m,
получим довер-ый интервал
для неизв-го мат-ого ожидания m норм-но распред-ой
случа-й
велич-ы X с
неизве-й диспер-й
 и задым уровнем
и задым уровнем
значи-ти
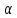 :
: