1)Пусть D-огран обл на пл-ти оху. f(х,у)-огран ф.,опред-я в обл D и пусть граница обл D -кус-но гладкая кривая.Выполним:1)разобьем обл D кус-но гладк дугами на l частн обл-тей D _i с площадями ΔS_i.

2)в кажд частичн обл D _i произв-но выберем т. и выч-м ;3)сост-м интегр сумму: 4)обознач верхн грань диаметров частн обл-тей d_i=sup ρ(

Если конечн предел инт-х сумм при λ0,независ-й ни от способа разбиения обл D,ни от выбора т.М_i,то этот предел наз-ся двойным интегралом от ф. f(x,y) по обл D и обознач-ся:

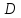Т.1:Если ф непрер в замкн обл ,то она интегр-ма в эт обл D

Т.2: Если ф 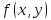кус-но непрер в обл D,то она интегр-ма в обл D

2)Св-ва:1)лин-ность:

2)

3)Аддитивность:

.

4)Если

5) Если g0,то 6)оценка модуля: 7)оценка инт-ла: если m=

8)Т о среднем:если f(х,у) непрер в замкн огран обл Д,то в этой обл найд-ся такая т.М( что вып-ся:S_D

Геом.смысл:пусть в простр-ве R₃ задано тело,огранич снизу плоск обл-ю ,по бокам цилиндр пов-тью с направл границей обл-ти ,а сверху графико непрер ф. z=f(х,у)≥0. Интегр сумма предст-т собой сумму объемов прямых цилиндров с основанием ΔS_i и высотами . Объем всего тела ≈этой интег сумме V≈ Переходя в этом приближ рав-ве к пределу(,получим что V_тела=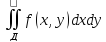-объем криволин цил-ра.S_L=-пл-дь обл

5)1)V цил-ра V= ; 2)S плоской фиг-ры: S= ; 3)масса пластинки с перемен поверх пл-тью 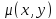: m= ; 4)коорд-ты центра тяж-ти пл-й пластинки: x_C=, y_C=; 5)Пл-дь пов-ти: пов-ть S задана ур-ем z=z(x,y), z(x,y)-непрер дифференц-мая ф. S пов-ти ч/з ∫∫: S_пов= ;если пов-ть задана неявно ур-ем F(x,y,z)=0, z=z(x,y), то учит-ся фор-лы z’_x = ; z’_y = ; получим: S_пов=

3)Вычисление ∫∫ сводится к послед-му вычислению обычн инт-лов:1)в случае прямоуг обл:пусть предст-т прямоуг-к :{а≤х≤в, с≤у≤d}.f(х,у) непрер в этом прямоуг-ке ф-я.Если у f(х,у) зафикс-ть перемен х,то получим ф-ю завис-ти только от у=> .Эт инт-л м расписать как ф-ю завис-ю от х=>=повторн инт-л. Ан-но опред-ся 2й повтор инт-л:=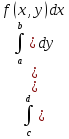

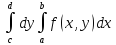
2)Случай криволин обл-ти Рас-м огран обл : пусть люб прямая || оси оу обл двух точках,такая обд наз-ся правильной в направл оси оу.Ан-но,опред-ся правильн обл в направл оси ох.Рас-м обл прав-ную в обоих направлениях. ∫∫ по обл по напр оси оу =повт-му:. Ан-но в напр ох:

7)1)лин-ность

2)

3)Аддитив-ть:

.

4)Если

5) Если g0,то 6)оценка модуля: 7)Оценка инт-ла:если непрер в обл V,m=,M=

mV_V MV_V,V_V-объем обл V

8)Т.о среднем:если f(x,y,z) непрер в обл V,то в этой обл такая т. М(х,у,z) / 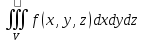=f(;

Вычис-е ∫∫∫ свод-ся к вычислению повторн инт-лов,если обл V задана нер-вами ,,, то .Таких повт ∫ 6. Если обл V явл правильной в направл всех осей,то эти 6 повт инт-лов =м/у собой и = ∫∫∫

4) треб-ся перейти к нов перемен по ф-лам:

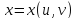
( * ) , при такой замене измен-ся не только подинтег-е выраж,но и обл D,т.е 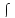полностью измен-ся. Предпол-м,что 1)перемен изм –ся в нек обл G на пл-ти 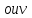; 2)ф. x( им непрер част произв в обл G. 3)Функц. опред-ль Якоби(якобиан) 0 ни в одной т. обл G. При таких предполож-х обл G на пл-тивзаимоодн-но отображ-ся в обл D на пл-ти оху,причем гранич т-ки переходят в гранич-е, а внутр-е во внутр-е.Выясним,как измен S обл при такой замене.Пл-ть -прям-к P,S_P=ΔuΔ

При замене (*) образом пр-ка Р явл. Криволин параллелограмм П. С точн-тью до ∞-но малых высш пор-ка S крив парал-ма П можно заменить на S обычного парал-ма,поострен-го на вектора . Найдем коор-ты этих векторов:

Найдем S парал-ма как ││вект-го произв-я S_n=| =|J|S_P|J|=. Т.о |J|=отношению ∞-но малых пл-ей соотв-х друг другу при замене (*).Выведем ф-лу преобр. ∫∫ призамене (*).Если ф.f(x,y) непрер в обл D, то ∫∫ и не завис от способа разбиения обл D,поэтому выберем такое разбиение,кот соот-т разб-ю обл G на прям-к.

ПП

Сост-м интег сумму:

Наиб распр-ной заменой для ∫∫ явл переход к поляр корд-м

При такой замене:

6)Пусть в замкнутой огран обл V задана непрер ф f(x,y). Разобьем область V на n элемент частей V_i. В кажд элем части V_i возьмем произв т. и вычислим f(). Обоз-м объем элем ячейки ч/з Δ и составим инт сумму .Пусть 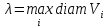.ОПР: если конечн предел инт-х сумм при λ0,независ-й ни от способа разбиения обл V,ни от выбора т.М_i ,то этот предел наз-ся 3-м интегралом от ф. f(x,y) по обл V и обознач-ся:

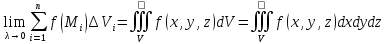
Необх усл 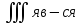огран-ть ф.в обл V, а достат усл-непрер-ть ф. в этой обл-ти

9)Начало в 8 вопросе

2)Сферические коор-ты:

Вычислим:

=

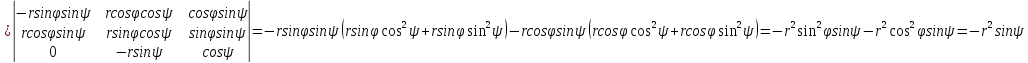
10)1)масса тела:если внутри обл V распред масса с некот непрер пл-тью (x,y,z),то масса тела: m= 2)Объем тела:если (x,y,z)=1,то масса тела числ-но=V этого тела V= 3) коор-ты центра тяж-ти: x_C=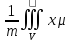(x,y,z)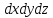; y_C=(x,y,z)

z_C=(x,y,z)

11)Экс-мент наз-ся случайным,если при повторении эксп-тов его рез-т невозможно предугадать. Всякий исход,кот может произойти или не произойти,в рез-те случ эксп-та и не мож быть наперед предсказан его появлением,наз-ся случ событием или случ явлением.Случайное соб –соб,кот может произойти, а может не произойти в рез-те эксп-та.Случ событие-случ исход опыта. Пр1:бросается кубик(возможно 6 исходов{1,2,3,4,5,6})Пр.2:монета подбрас-ся 2 раза возм-ны след исходы(гг,гр,рг,рр);Пр.3: (подбрасывание монеты)т.к заранее неизв-но какой стороной выпадет монета,то этот эксп-т случ-ный,имеет 2 исхода:герб-решетка. Т.к невозм-но заранее предсказать,что выпадет,то выпадение г-р явл случ соб-ем; Пр.4:монета бросается пока не вып-т герб,исходы {г,рг,ррг,рррг,…} Число исходов ∞-но,но счетно,т.е их число соот-ет числу натур ряда. Пр.5:стрельба по плоск мишени,т.к точки попадания заранее неизвестны,то это случ эксп-т,число исходов несчетно.

8)Пусть некот преобр-е коор-т в простр-ве задано сис-мой:

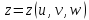; x,y,z-непрер диф-мые. Если J=0 ни в одной т-ке обл V,то указ преобраз-е коор-т взаимооднозначно отображ обл V в обл ,причем гранич т-ки переходят в гранич-е, а внутр-е во внутр-е.Ан-но ∫∫ ф-ла замены перемен-х в ∫∫∫ им вид:

Цилинд-е коорд-ты: если полярность на пл-ти оху совпад-т с ох,то цилиндр-е коор-ты предст-т собой практич полярн корд-ты + ось оz:

Выч-им J при переходе к цилин-м коор-там.

J==

=>|J|=r

12)Тео́рия вероя́тностей — наука, изучающая закономерности случайных явлений их свойства и операции над ними.Изучает явл-я объединенные св-вами:а)массовости-явление мож быть осуществ-но неогран число раз причем в неизмен усл-ях б)статической устойчив-ти(Пр:если много раз подбрас-ть монету,то частота появл герба постепенно стабилизир-ся и приближ-ся к ½).Множ-во всех возмож взаимоисключающих исхода случ эксп-тов наз-ся пространством элемент событий.Элемент этого множ-ва наз элементар событием и обозн-ся .Из опред=> что при проведении опыта обяз-но произ-дет одно из элемент событий и никакие 2 элем соб-я не могут произойти одновр-но в рамках одного и того же эксп-та.ОПРЕД:случ соб-ем( в теоретико-множ-ом смысле)наз-ся любое подмнож-во пространства элем соб,если прост-во эл соб-й конечно или счетно.Случ соб обозн-ся больш лат буквами А,В,С…А.Мощностью сл соб-я наз число элем исходов из кот оно состоит. -мощность соб А. ПР:(кубик)

13) Суммой двух событий А и B () называется событие, состоящее в том,что при проведении опыта произ-т соб А или В,или оба соб-я

Произведением

() событий А и B называется событие, состоящее в том,что при провед-и экс-та произойдут и А и B.

Разностью (А\B) А–B событий А и B называется событие, состоящее в том,что при провед экс-та соб А происх-т,а В нет.

14. Будем предполагать: 1.пространство элементарных событий конечно и невозможно.2.Исходы случайного эксперимента равновозможны.3.Понятие равновозможности является первичным и не подлежит формальному определению.

Равновозможность обозначает симметрию исходов в условиях опыта, когда нет основания считать 1 исход более вероятным, чем другой. Т.е. игральная кость должна быть кубом, шары в урне должны иметь одинаковый размер.

Пусть:1) - простр. элемент. событий.

; 2)A;,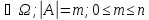

Определение: вероятностью события А называется величина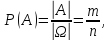 , где n-общее число всех возможных элементарных исходов испытания, благоприятствующих появлению события А.

Св-ва вероятностей:

1.; ;; n>0

2.

3.

4.если события А и В несовместны, то P(A+B)=P(A)+P(B), т.е. вероятность появления хотя бы 1 из 2 возможных соб-й = сумме вер-тей этих соб-й.

Док-во: Пусть n –общее число всех исходов испытания;-число элементарных исходов испытаний, благоприятствующих появлению события А;-число… события В;Т.к. события А и В несовместны, то число исходов благоприятствует появлению события А, отлично от числа исходов, благоприятствующих появлению события В. Тогда число исходов, благопр. Появлению события А+В равно: и вер-ть=:

P(A+B)=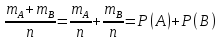

5.P(A)+P(; Док-во:A+,события А и -несовместны, поэтому

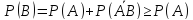
6.если A, то Док-во:B==(A+, события А и - несовм., поэтому P(B)=P(A)+P(

В конкретных задачах по определению вероятностей простых элементарных событий строится на проведении аналогии м/у рассмотренным экспериментом и какой-либо хорошо изученной моделью случайного явления. Наиб. распростран. является классическая вероятностная схема выбора.

15. Классическая вероятностная схема выбора. Упорядоченные выборки с повторениями и без повторений.

Пусть в урне находится n шаров одного размера, пронумерованные{1;2;3;..n}.На удачу из урны извлекают m шаров.

Упорядоченная выборка с повторениями: шары возвращаются обратно в урну и при этом учитывается № вынутого шара. Общее число всех упорядоченных выборок с повторениями наход. По ф-ле: N(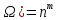

Упорядоченная выборка без повторений: шары не возвращаются в урну обратно, но учитывается порядок вынутых шаров. Общ. число всех упоряд. выборок без повторений опред. ф-лой:

N( - число размещений из n по m. В частности, если m=n, то получается число перестановок из n-элементов. P_n=n!- число перестановок.

16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.

Пусть в урне находится n шаров одного размера, пронумерованные{1;2;3;..n}.На удачу из урны извлекают m шаров.

_{Неупорядоченная выборка с повторениями}: шары возвращаются обратно в урну, но при этом не важен порядок вынутых шаров. Общ. число неупоряд. выборок с повторениями опред. ф-лой: N(

Неупорядоченная выборка без повторений: шары обратно не возвращаются (т.е. нет повтора), не важен порядок вынутых шаров. Общ. число неупоряд. выборок без повторений опред. ф-лой:

N(

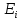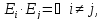Разбиение на k-подмножеств: пусть множество E, состоит из n-элементов(), следует разбить на k-подмножеств,,, ,так, что и, без учёта порядка элемента. Тогда общее число таких разбиений находится по ф-ле:. N(

18.Сложение вероятностей несовместных событий: вер-ть появления хотя бы одного из двух несовместных событий (AB=Ф) равна сумме вер-тей этих событий, т.е.:P(A+B)=P(A)+P(B). Следствие: вер-ть появления хотя бы одного из n попарно несовместных событий, равна сумме вер-тей этих событий:.

_{Сложение} вероятностей совместных событий: вер-ть появления хотя бы одного из двух совместных событий (AB) равна сумме вер-тей этих событий без вер-ти их совместного появления: P(A+B)=P(A)+P(B)-P(AB). Док-во: пусть А и В – совместны, т.е. AB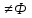, представим событие (A+B) в виде суммы трёх несовместных вариантов:

(1), A=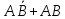-несовм, P(A)=P(, т.к. в правой части (1) представлены несовместные события, то , в эту ф-лу подставим значения и, получим:

P(A+B)=P(A)-P(AB)+P(B)-P(AB)+P(AB), т.е. P(A+B)=P(A)-P(AB)+P(B), Ч.Т.Д.

Эту теорему можно обобщит для любого числа событий: P(A+B+C)= P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC), а для n событий теорема выглядит так:P(