- •1.1 Расчет мощности на валах
- •1.2 Подбор электродвигателя
- •1.3 Определение общего передаточного отношения
- •1.4 Определение частот вращения валов редуктора
- •2 Расчет зубчатых передач редуктора.
- •2.1 Выбор материала зубчатого колеса и обоснование термообработки
- •2.2 Определение допускаемых напряжений
- •2.3 Определение допускаемых напряжений изгиба
- •2.4 Расчет цилиндрической передачи (2-я ступень)
- •2.4.1 Определение основных геометрических параметров цилиндрической передачи.
- •2.4.2 Проверочный расчет передачи на контактную прочность.
- •2.4.3. Расчет на усталость по изгибу
- •2.5 Расчет конической передачи
- •2.5.1Определение основных геометрических параметров конической передачи.
- •2.5.2 Проверочный расчет передачи
- •3.Определение диаметра валов и подбор подшипников качения
2.3 Определение допускаемых напряжений изгиба
Допускаемые напряжения изгиба для зубчатых колёс определим по формуле:
[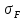 ]
=
]
=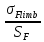 ·KFL
·KFC
·KFL
·KFC
Flimb j - базовый предел выносливости по изгибу.
SFj - коэффициент безопасности.
KHLj - коэффициент долговечности,
Согласно рекомендации [1] определяем Flimb и SF:
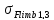 =
1,8 · HB1
=
1,8 ·230 = 414 МПа.
=
1,8 · HB1
=
1,8 ·230 = 414 МПа.
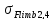 =
1,8 ·НВ2
=
1,8 ·200 = 360 МПа.
=
1,8 ·НВ2
=
1,8 ·200 = 360 МПа.
SF 1,7 2,2, принимаем SF1,2,3,4 1,7.
Базовое число циклов NF0 4106
Расчетное число циклов перемены напряжений определим по формуле: NFEj 60Cj nj th,
для колеса z1:
NFE1 NHЕ1 601300035000 6,3·109
для колес z2 и z3:
NFE2 NFE3 NHЕ2= NHЕ3 6011200 35000 2,52109
для колес z4:
NFE4 NHЕ4= 601400 35000 0,84 109.
Так как NFE1,NFE2,NFE3,NFE4 >NFO , то KFL1 =KFL2 =KFL3 =KFL4 =1
Поскольку зуб работает одной стороной, то KFL1 =KFL2 =KFL3 =KFL4 =1
Определяем
[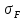 ]:
]:
[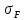 ]1
=
]1
=
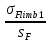 ·KFC·KFL=
·KFC·KFL=
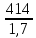 · 1·1 = 243,53 МПа.
· 1·1 = 243,53 МПа.
[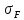 ]2=
]2=
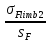 ·KFC·KFL
=
·KFC·KFL
=
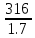 ·1·1 = 185,9 МПа.
·1·1 = 185,9 МПа.
В качестве допускаемых напряжений изгиба для передачи принимаем меньшее значение из двух полученных:
[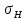 ]1=
391,4 МПа.
]1=
391,4 МПа.
[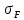 ]1
=
= 185,9 МПа.
]1
=
= 185,9 МПа.
2.4 Расчет цилиндрической передачи (2-я ступень)
2.4.1 Определение основных геометрических параметров цилиндрической передачи.
Определяем межосевое расстояние:
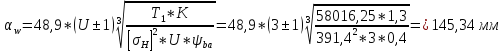
где
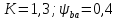 .
.
Рассчитываем геометрические параметры колес:
рабочая
ширина колеса:
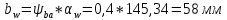 .
.
задаем коэффициент формы зуба эквивалентного колеса согласно [1]:
торцевой
модуль:
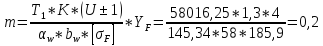
округляем по ГОСТ, но не меньше mmin = 1,5 мм
Принимаем модуль m = 1,5 мм.
где
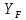 –
предварительно принятый коэффициент
формы зуба.
–
предварительно принятый коэффициент
формы зуба.
Для
седьмой степени точности
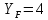 .
.
Число
зубьев шестерни:
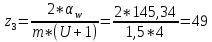
Тогда
число зубьев колеса:
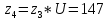 .
.
Относительное
отклонение полученного передаточного
числа от принятого:
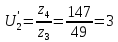
Погрешность:
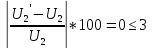 .
.
Уточняем размеры диаметров делительных окружностей:
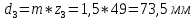
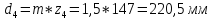 .
.
Определяем межосевое расстояние:
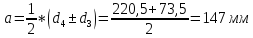 .
.
2.4.2 Проверочный расчет передачи на контактную прочность.
Проверим зубчатую передачу на выносливость от действия контактных напряжений.
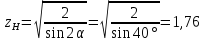
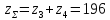
zΣ=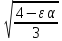 =
=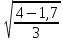 =0,875
=0,875
шестерни:
d3 = 73,5 мм.
da3 = d3+2m = 76,5
df3 = d3-2,5m = 69,75
db = d1 ·cos α = 69,07
колеса:
d4 = 220,5 мм
da2 = d2 +2m = 223,5
df4 = d4 – 2,5m = 216,75
db4= d4·cos α = 162 ·cos 20 = 207,2
Уточним величину коэффициента динамической нагрузки [1]. Для этого рассчитываем окружную скорость в зацеплении:
V=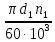 =
=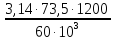 = 4,62 м/с
= 4,62 м/с
и назначаем 7-ю степень точности [1].
коэффициент динамической нагрузки Kv = 1,35
KHα=1
Kβ =1,15
по таблице №7
=1,15
по таблице №7
Kβ=1
Кv-коэффициент динамичности
Кv=1,45
Кн=
KHα Kβ
Kβ
 Кv=1
Кv=1
 1
1
 1,45=1,45
1,45=1,45
Коэффициент торцевого перекрытия Eα определим по формуле:
Eα
=
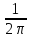 (z3
·tgαa3
+ z4·tgαa4
– (z3+z4)tgaw)
(z3
·tgαa3
+ z4·tgαa4
– (z3+z4)tgaw)
Eα
=
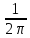 (
49·0,541 + 147·0,433 – (147+49)·0,364) = 1,7.
(
49·0,541 + 147·0,433 – (147+49)·0,364) = 1,7.
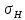 ≤[
≤[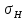 ]
]
σн=275
 zн
zн
 zΣ
zΣ

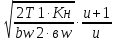 ;
;
Т1-проектный расчет
Т1=58016,25
(Н
 мм)
мм)
Кн=1,6
U=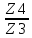 =
=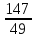 =3
=3
Принимаем
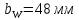
σн=275
 1,764
1,764 =370,9
Мпа ≤ [
=370,9
Мпа ≤ [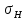 ]=391,4
Мпа
]=391,4
Мпа
2.4.3. Расчет на усталость по изгибу
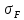 ≤[
≤[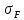 ];
];
YF3=3,62
YF4=3,6
σF3=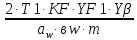 ≤
[
≤
[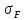 ]1
;
]1
;
σF4
=
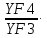 σF3≤
[
σF3≤
[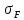 ]2
;
]2
;
σF3=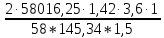 =46,91≤[
=46,91≤[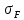 ]1=185,9
МПа
]1=185,9
МПа
σF4
=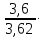 46,91=46,65Мпа
≤ [
46,91=46,65Мпа
≤ [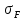 ]2
= 185,9 МПа
]2
= 185,9 МПа
2.5 Расчет конической передачи
2.5.1Определение основных геометрических параметров конической передачи.
NE1=60
 n1
n1
 c
c
 th
th
 KHE
KHE
NE2=60
 n2
n2
 c
c
 th
th
 KHE
KHE
KHE=1
NE1=60
 3000
3000 1
1 35000
35000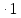 =6,3
=6,3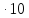 9
9
NE2=60
 1200
1200 1
1 35000
35000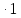 =2,52
=2,52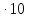 9
9
[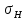 ]1=441,6
МПа
]1=441,6
МПа
[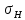 ]2=391,6
Мпа
]2=391,6
Мпа
[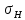 ]min=[
]min=[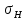 ]2=391,6
Мпа
]2=391,6
Мпа
Проектный расчет
dm1=Kd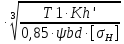 2
2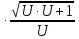 ;
;
U=U1=2,5
Kd=77 т.к. 7 степень точности,
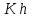 '=1,5
'=1,5
ψвd=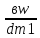 =0,5
=0,5
dm1=77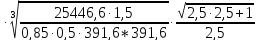 =69,4мм
=69,4мм
вw=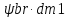 =0,5
=0,5 69,4=35
69,4=35
ψвd=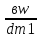 =0,5,следовательно
Кβ°=1,25
табл.6
=0,5,следовательно
Кβ°=1,25
табл.6
Кβ=0,5(Кβ°+1)=0,5(1,25+1)=1,125
Кн=
Кн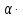 Кβ
Кβ Кv=1,25
Кv=1,25
Определяем модуль:
mte=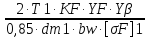
KF=
KF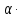 Кβ
Кβ Kv=0,91
Kv=0,91 1,125
1,125 1.45=1,48
1.45=1,48
mte=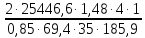 =0,78мм
=0,78мм
Примем mte=2 мм
z1=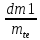 =69,4/2=35
=69,4/2=35
z2=
z1 U1=35
U1=35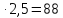
U1ср=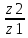 =88/35=2,5
погрешность 0%
=88/35=2,5
погрешность 0%
U1=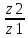 =2,5
=2,5
U1=1,5
tgδ1=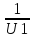 =1/2,5=0,4,следовательноδ1=21,8
=1/2,5=0,4,следовательноδ1=21,8
δ2=90-21,8=68,2
mtm= mnm=2,5 мм
Re=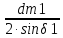 =
=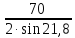 =1,48
=1,48
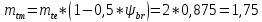
dm1=
mtm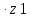 =1,75
=1,75
 35=61
35=61
dm2=
mtm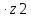 =1,75
=1,75 88=154
88=154
de1=
mte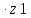 =2
=2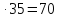
de2=
mte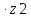 =2
=2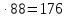
tgθa=
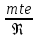 следует, чтоθa=1,35
следует, чтоθa=1,35
tgθf=
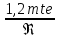 =
=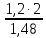 =1,62
=1,62
δa1=δ1+θa=21,8+1,35=23,15
δa2=δ2+θa=68,2+1,62=69,82
δf1=δ1+θf=21,8-2.29=19,51
δf2=δ2+θf=68,2-2,29=65,91
dae1=de1+2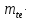 cos
cos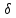 1=70+2
1=70+2 2
2 cos21,8=73,7
cos21,8=73,7
dae2=de2+2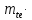 cos
cos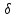 2=176+2
2=176+2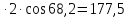
B1=0,5 de2-
de2-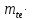 sin
sin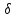 1=0,5
1=0,5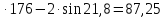
B2=0,5 de1-
de1-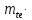 sin
sin 2=0,5
2=0,5