5. Методы формализации постановки задач принятия решений
- интуитивный метод
- метод экономическо-математического моделирования
Наука – формальные методы, логическое построение которых позволяют принять управленческие решения.
Пример: талантливые люди, основываясь на известной информации, полагаясь на свой опыт и умение, принимали управленческие решения
Ф(х,а) max
Как формализовать задачу принятия решения:
1 этап: Описывается исследуемая система: определяется ее целевое назначение, характер деятельности, характер выпускаемой продукции, используемые ресурсы, описываются нормативные параметры, ограничения внешние и внутренние.
2 этап: Введение элементов формалистики: вводятся переменные(управленческие решения, которые будут искаться), вводятся параметры и формализованные обозначения, вводятся индексы, формулируется математическая запись критерия управления и система ограничений+ математическая постановка задачи
Ф(х) – мах - критерий
х € Х - с-ма ограничений
3 этап: В зависимости от полученной конструкции выбираем метод решения задачи
4 этап: Решение задачи, получение результатов. Хj0 – оптимальное решение (экстремум целевой функции)
5 этап: Анализ полученных результатов и оценка их адекватности реалиям. Если результаты не соответствуют реальности, то возврат на пункт 1.
Пример: измеряли связь между температурой верха колонны и качеством полученного изделия, основываясь на статистических данных, выяснили, что коэффициент корреляции=0(значит связи нет), а в реальности(на практике) качество продукции регулируется именно температурой верха колонны.
Пример: 1 этап: Имеется предприятие, которое выпускает определенную номенклатуру образцов. При выпуске продукции используются определенные ресурсы. Известны нормативы затрат каждого вида ресурса на производство 1 штуки каждого вида продукции. Имеется информация о запасах каждого вида ресурса. Имеется информация о ценах, по которым мы реализуем каждый вид продукции. Необходимо найти оптимальную производственную программу, которая обеспечила бы максимум выручки или дохода.
2 этап: х – количество выпускаемой продукции
j – номер конкретного вида продукции
n – количество видов продукции j=от 1 до n
Xj – количество продукции j-го вида, которое мы будем выпускать
Сj – цена, по которой будет выпускаться j-й вид продукции
Ф=
- выручка от продукции
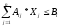
–сколько i-го
ресурса мы потратили, произведя все
ресурсы
i = от 1 до m
Aij – сколько нужно ресурсов i-го типа, чтобы произвести j-ю продукцию в количестве 1 штуки
Bi – запас ресурса i-го вида, которым мы располагаем
6. Постановка задач принятия упр.Решений в классе линейных моделей
Существуют определенные правила, которыми следует руководствоваться, чтобы сформулировать задачу.
Постановка управленческой задачи включает в себя 2 элемента:
- Критерии задач (орган управления должен четко сформулировать, что он хочет).
- Ограничения (внешние и внутренние).
Лицо, принимающее решения, имеет возможность влиять на ограничение.
Ф(х) – некоторый критерий.
х – параметры, которые мы пытаемся активизировать.
Задача.
Имеется предприятие по производству колбасы. Мы можем выпускать 2 вида колбасы:
- вареную;
- ветчинно-рубленную.
Цена вареной колбасы 120 руб.
Цена ветчинно-рубленной – 200 руб.
Для производства этих колбас используется 3 вида ресурсов:
- говядина,
- свинина,
- горох.
На складе имеются следующие запасы этих ресурсов:
- говядина – 100 кг.,
- свинина – 60 кг.,
- горох – 200 кг.
Известны нормативы затрат каждого вида ресурса на производство единицы продукции:
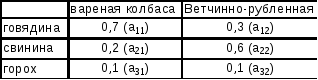
Ставится задача: Лицо, принимающее решения, должно составить план выпуска продукции так, чтобы уложиться в ограничение и обеспечить максимум стоимости выпускаемой продукции.
Введем переменные:
x – количество выпускаемой продукции,
j – номер выпускаемой продукции, j=1,2,
Тогда хj – количество продукции j-го типа, которое мы должны определить.
b – количество ресурса, которым располагает ЛПР.
i – номер ресурса, i=1,3,
Цj – цена за 1 ед. j-го типа продукции,
bi - количество ресурсов i-го типа, которыми распоряжается ЛПР,
а – норматив затрат ресурса,
аij – показывает сколько единиц i-го ресурса требуется для производства 1 шт. j-той продукции.
Задачи, в которых переменные и критерии и в ограничениях находятся в первой степени, называются задачами линейного программирования.
Задача в общем виде:
- количество
говядины, которая потребуется, чтобы
реализовать нашу продукцию,
- количество свинины,
которая потребуется, чтобы реализовать
нашу продукцию,
- количество гороха,
который потребуется, чтобы реализовать
нашу продукцию.
Общий вид задачи:
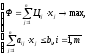
120х1 + 200х2 → max
0,7х1 + 0,3х2 ≤ 100
0,2х1 + 0,6х2 ≤ 60
0,1х1 + 0,1х2 ≤ 200.
Решим задачу методом геометрической интерпретации:
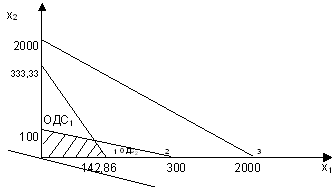
ОДС1 – если смотреть на задачу через призму только 1-го ограничения (говядины),
ОДС2 – если смотреть на задачу через призму только 2-го ограничения (свинины).
Построим прямую Ф=0. Точка, максимально удаленная от прямой Ф=0 – точка оптимума.
Оптимальное решение находится на пересечении условий (пересечение условий говядины и свинины).
0,7х1 + 0,3х2 = 100
0,2х1 + 0,6х2 = 60,
Точка оптимума имеет координаты
х1 = 117
х2 = 61
Резерв по ресурсу – это разность между запасами с сколько надо потратить.
у1 = 0
у2 = 0 резервные ресурсы.
У3 ≠ 0 – недефицитны ресурс.