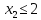Laboratornaya_rabota_6

Лабораторная работа №6

Решение задач целочисленного линейного программирования в табличном процессоре Excel.

Цель работы: изучение математической модели задачи целочисленного линейного программирования, освоение технологии решения ЗЦЛП в табличном процессоре Excel.

Содержание лабораторной работы

Дана ЗЦЛП. Требуется найти решение задачи методом «ветвей и границ» с помощью встроенной функции «Поиск решения» табличного процессора Excel.

Задание: вариант 5

Математическая модель

ЦФ: F = 10x₁+13x₂ max

Система ограничений:

Составим каноническую форму записи

Рисунок 1 - Результат после выбора опции целое

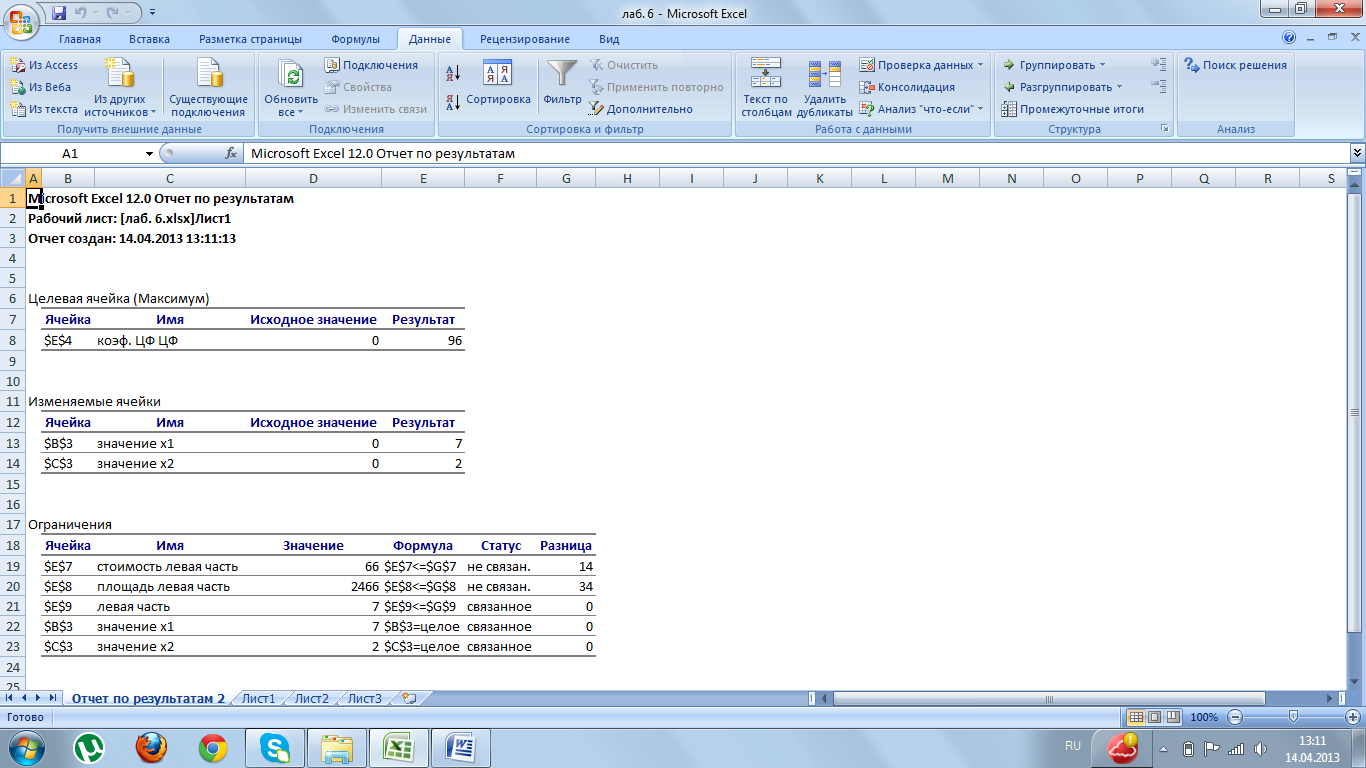
Рисунок 2 - Отчет по результатам

Получились целые значения: х1=7, х2=2. Значение целевой функции находится в ячейке Е4: f=96. Оптимальным будет вариант, при котором приобретаются 7 машин типа А и 2 машины типа В. При этом 14 д.е. и 34 м² площади останутся неиспользованными. Максимальная производительность будет составлять 96 ед. продукции.

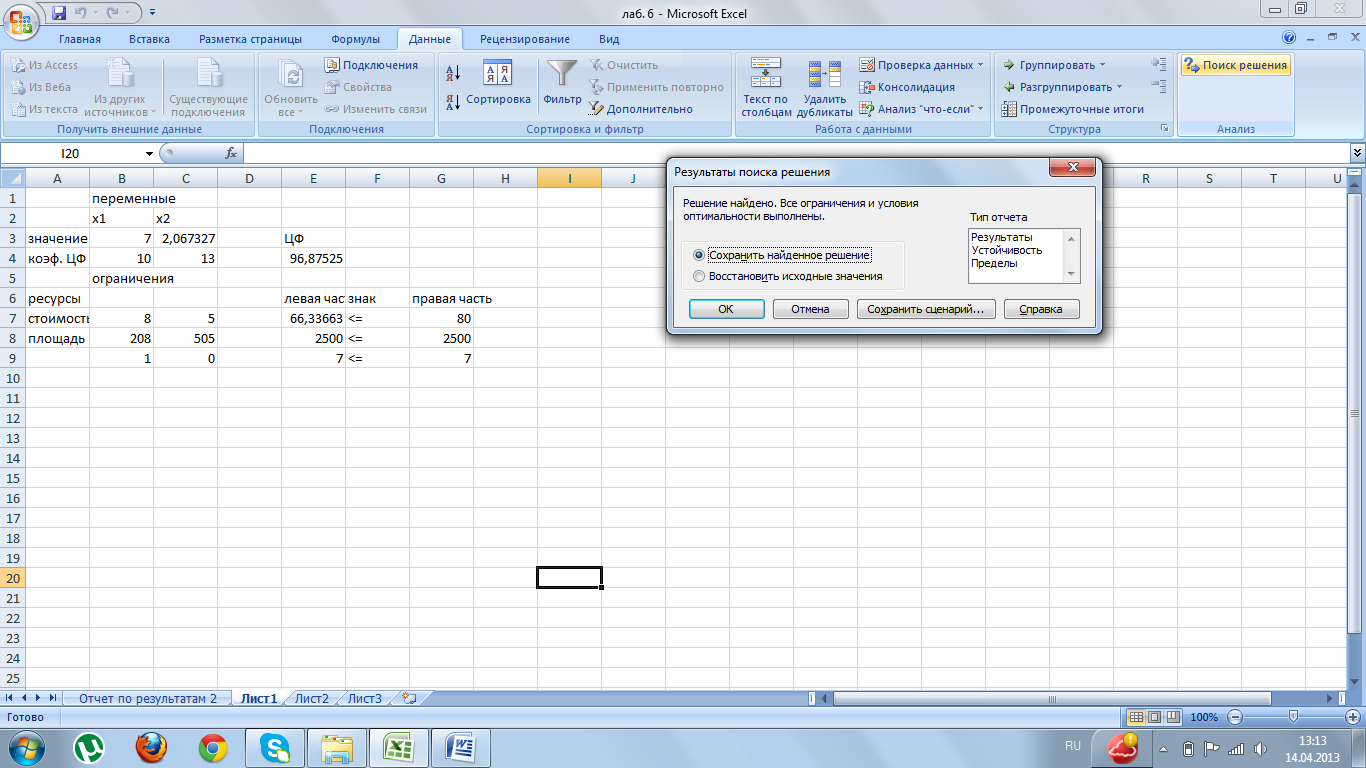
Рисунок 3 - Решение исходной задачи

1.1

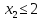
1.2

Рисунок 4 - Решение подзадачи 1.1

В результате решения подзадачи 1.1 получили решение: х₁=7, х₂=2. Значение целевой функции: f=96. Оно является нижней границей целевой функции.

Рисунок 5 - Решение подзадачи 1.2

В результате решения подзадачи 1.2 получили решение: х₁=4,735577, х₂=3. Значение целевой функции: f=86,35577. Рассматривать эту ветвь дальше не имеет смысла, т.к. значение целевой функции f=86,35577 меньше нижней границы ЦФ (f=14).

Найдено оптимальное решение задачи: х_ц^опт=(7;2), f(х_ц^опт)=96.

Ход решения:

0. Ответ: х1=7, х2=2,067327 ЦФ: f=96,87525
1.1 Ответ: х1=7, х2=2 ЦФ: f=96	1.2 Ответ: х1=4,735577, х2=3 ЦФ: f=86,35577

Ответы на контрольные вопросы:

1. Под ЗЛЦП понимается задача, в которой все или некоторые переменные должны принимать целые значения.

2. Метод «ветвей и границ», метод Гуморя или метод отсечений, с помощью Поиска решений в табличном процессоре Excel с указанием условия целочисленности искомых переменных.

3. Пусть хi – целочисленная переменная, значение хi^* которой в оптимальном решении исходной задачи является дробным. Рассмотрим интервал [x_i^*]<x_i<[x_i^*]+1. Он не содержит допустимых целочисленных компонент решения. Поэтому допустимое целое значение х_i должно удовлетворять одному из неравенств: Два последних неравенства разбивают область допустимых решений для переменной х_i на две подобласти. То есть исходная задача разветвилась на две подзадачи, каждая из которых решается отдельно от ЗЛП с целевой функцией исходной задачи.

4. Целевая функция соответствует ЦФ исходной задачи, система ограничений остается прежней и к ней добавляются новые условия относительно хi: интервал [x_i^*]<x_i<[x_i^*]+1 не содержит допустимых целочисленных компонент решения. Поэтому допустимое целое значение х_i должно удовлетворять одному из неравенств:

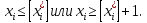
5. В качестве верхней границы на множестве планов рассматривают значение целевой функции без условий целочисленности.

6. Математическая модель ЗЦЛП:

Z – множество целых чисел. Если p=n, то задачу называют полностью целочисленной, если p<n, то частично целочисленной.